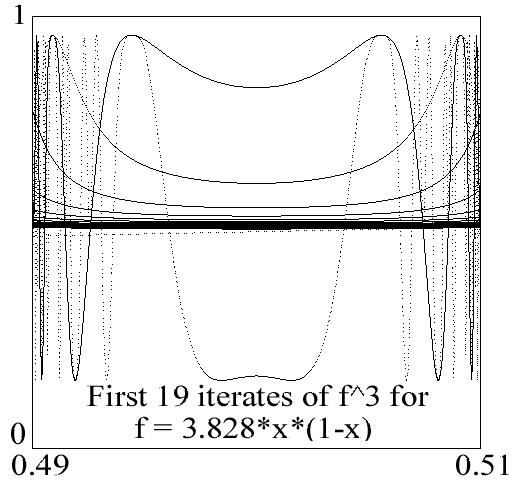
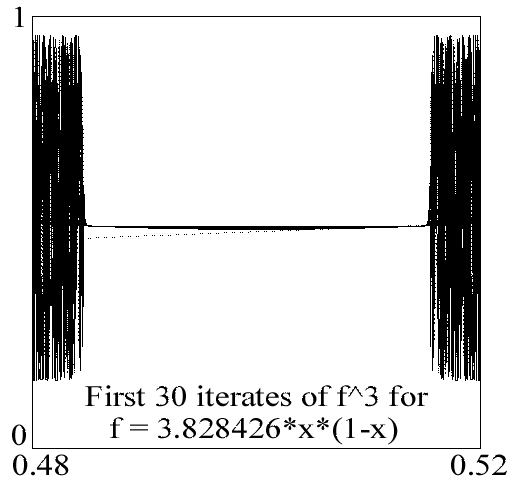

Intermittancy between chaos and order in logistic map for l<l*=3.828426. The plots display graphical convergence of the iterates of f3
http://kermani.math.fit.edu/wcna2000/program.html
University of Catania, Catania, Sicily, Italy, July 19-26, 2000
Invited Lecture at main session
Ill-Posed Problems, Multifunctions, and Chaotic Dynamical Systems
Abstract
.
This talk will present a new formulation of one-dimensional discrete chaotic systems based on the concepts of an ill-posed problem f(x) = y where x and y are elements of a topological space X, and a multifunctional limit Multi(X) of a sequence of functions (fi) in Map(X) that will be constructed as the graphical limit of a sequence of functions. This topological extension of Map(X) is the central ingredient of our appraoch and depends on a pointwise bi- convergence of the sequence. The ill-posedness of importance to us arises from the non- injectivity of the sequence of functions, and the multifunctional inverse of f that is obtained from its generalized inverse G is basic to our theory. We show that a notion of maximal ill-posedness of the sequence of iterates of f is equivalent to chaos of the discrete dynamical system. The following illustration is a typical example of our results.



Intermittancy between chaos and order in logistic map for l<l*=3.828426. The plots display graphical convergence of the iterates of f3
The tangent bifurcation at
l* is characterized by the graphical convergence of the iterates of f3 to a middle horizontal portion as shown in the second figure. The complete formal similarity of these figures to the following set for the graphical convergence of the non- chaotic family of iterates of lx2sin(px) displaying tangent bifurcation is to be noted.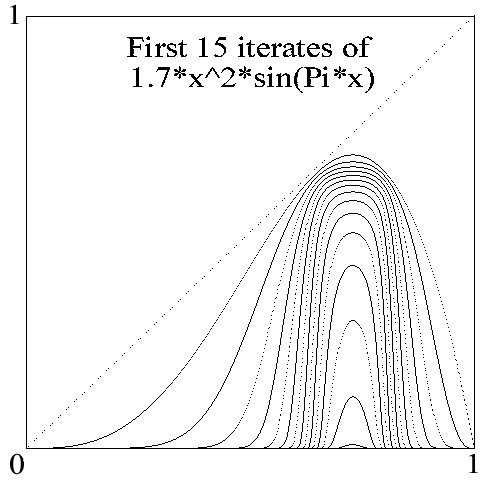
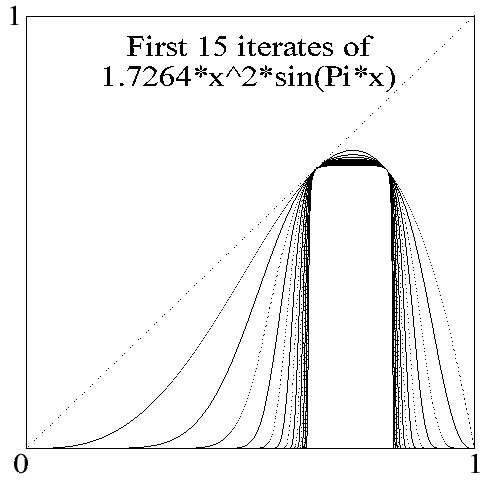
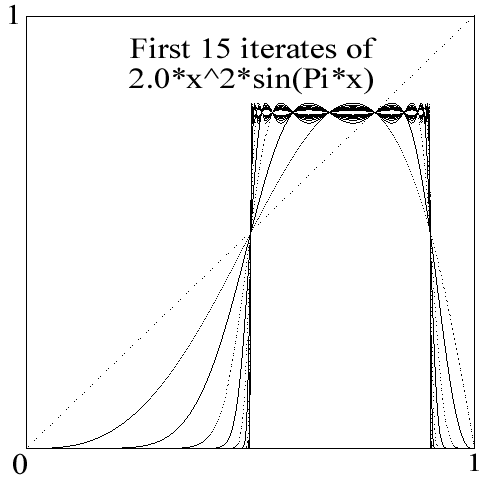
Saddle-node bifurcation for the iteates of lx2sin(px).
References.
[1]. A. Sengupta, Multifunctions and generalized inverse, Jour. Inverse and ill-Posed Problems, 5, 265-285(1997).[2]. A. Sengupta and G. G. Ray, A multifunctional extension of function spaces: Chaotic dynamical spaces are maximally ill-posed,Jour. Inverse and ill-Posed Problems, Accepted.
[3]. A. Sengupta, Ill-posed problems, multifunctions and chaotic dynamical systems, Lectures at Workshop on Nonlinear Analysis and Its Applications, Calcutta 1999.
Organized Session:
ILL-POSED PROBLEMS AND COMPLEX DYNAMICAL SYSTEMSby
|
|
INDIAN SOCIETY OF NONLINEAR ANALYSTS |