

ME 698G



Announcements
-
(i)Keep a copy of the background material containing mathematical preliminaries and basic continuum mechanics during the lectures.
-
(ii)Please read above notes. Review if you have read above material before through some books or as a part of some courses.
-

Course details
Course No: ME 698G
Instructor: Basant Lal Sharma
Department: Mechanical Engineering
Units: (L-T-P-D-U) 3-0-0-0-4
Schedule: LEC: WTh 5:00-6:30pm FB370
Prerequisite: Introductory course on continuum mechanics or self study of theory of nonlinear elasticity, basic course containing a discussion of calculus of variations, exposure to theory of crystallography is a plus.
Note: The course is offered and structured as an (open) elective for postgraduate students and advanced undergraduate students. Anyone else interested may take permission of the instructor.

MY CONTACT
Email: bls at iitk.ac.in
Phone: 6173
Office: FB 356

Books
-
1.Bhattacharya, K., 2004. Microstructure of Martensite: Why It Forms and How It Gives Rise to the Shape-Memory Effect. Oxford University Press [Textbook: Chapters 1--9 only].
-
2.Pitteri, M. and Zanzotto, G., 2003. Continuum theories for phase transitions and twinning in crystals. Chapman and Hall.
-
3.Abeyaratne, R., Knowles, J. K., 2006. Evolution of Phase Transitions. A Continuum Theory. Cambridge University Press, New York.
-
4.Khachaturyan, A. G., 1983. Theory of Structural Transformations in Solids. John Wiley and Sons, New York.
-
5.Wayman, C. M., 1964. Introduction to the crystallography of martensitic transformations. Macmillan company, New York.
-
6.Gurtin, M. E.,1982. An Introduction to Continuum Mechanics, Academic Press.

Useful links
http://cst-www.nrl.navy.mil/lattice/
http://www.msm.cam.ac.uk/phase-trans/teaching.html
http://courses.theophys.kth.se/5A1335/
http://en.wikipedia.org/wiki/Point_groups_in_three_dimensions
Course Summary
We will study the stress induced structural (displacive) phase transformations in this course, with an emphasis on development of a rigorous mathematical theory of austenite-martensite phase transformation. Continuum theory for phase transitions and twinning in crystals, developed over the last three decades, has been a remarkably successful approach in which a new viewpoint on material symmetry, motivated by atomistic theories, plays a central role. This course will utilize a nonlinear elastic approach to twinning and displacive phase transition in crystalline solids. We will develop geometry, kinematics, and symmetry/invariance in crystals with the purpose of investigating the actual mechanical aspects of the phenomena, particularly in an elastostatics framework with some discussion of dynamics as well (if time permits). We will discuss the applications of this theory to the special case of shape memory alloys where the theory aims at investigating the formation of microstructures. Relevant to a variety of disciplines, including mathematical physics, continuum mechanics, and materials science, such course on continuum models for phase transitions and twinning in crystals is an opportunity to explore these current research methods and topics.
Contents
-
(i)Review of basic concepts in continuum mechanics and the theory of nonlinear elasticity. Discussion on a purely mechanical theory vs thermomechanical continuum theory.
-
(ii)Introduction to some crystallographic concepts and their representations, for example, crystallographic symmetries. The Cauchy-Born hypothesis and Ericksen-Pitteri neighbourhoods.
-
(iii)Martensitic phase transformation: one dimensional nonlinearly elastic (mechanical theory) and nonlinearly thermoelastic (thermomechanical theory) models: equilibria, quasistatic process, and introduction to the study of dynamics, energy minimization (energy wells) based approach for study of equilibria using calculus of variations. Discussion on shock wave motion vs phase boundary motion.
-
(iv)Martensitic phase transformation: three dimensional thermoelastic models: introduction to the study of equilibria, quasistatic process, and dynamics. If time permits, the three dimensional case may be explored further. Martensitic variants: twinning. Austenite-Martensite interface.
-
(v)Discussion on the Shape-memory effect.
-
(vi)Discussion on discrete models vs continuum models for the study of phase transformations.
-
(vii)Conclusion of the course with discussion on some open problems in the mathematical theory of martensitic phase transformations.
-
(viii)*There may be a few guest research seminars in this course, given by various professors, in order to motivate this subject. Two or more such lectures will discuss the importance and applications of this subject in different branches of engineering, metallurgy and materials processing, designing new materials by combining various elements as well as their phases through a thermomechanical process resulting in some interesting geometries at small and large scales coupled with interesting mechanical behavior. In addition to the latter, some future directions will also be discussed in the context of scientific research as well as applications of this subject. A few lectures or reading assignments may be devoted to some interesting results in the theory of martensitic phase transformation which find application in diverse areas of engineering and sciences such as shape memory alloys.
Theory of Martensitic Phase Transformation
Some information on Lectures
-
(I)Lecture 0 (29 Dec): Quiz for certain preliminaries, Overview of Course
-
(II)Lecture 1, 2 (31 Dec, 2 Jan): Review of some basic concepts in continuum mechanics and the theory of nonlinear elasticity: body and reference configuration, deformation and motion, deformation gradient, rotation tensors, stretch tensors and Cauchy-Green tensors, change of length, area, and volume, stretch ratios and stretch directions, constitutive relations and assumptions, material frame indifference, (simple) elastic material.
-
(III)Lecture 3, 4, 5, 6, 7 (5, 7, 9, 12, 14 Jan): Concepts and Definitions in Continuum Thermodynamics, Energy equation and Clausius-Duhem inequality. Discussion on a purely mechanical theory vs thermomechanical continuum theory. Discussion on Thermoelasticity and the consequences of postulate of material frame indifference and the postulate of material symmetry.
-
(IV)Lecture 8, 9, 10, 11 (16, 21, 22, 28, 29 Jan): Simple Lattices, Review of the notion of a Group and some useful theorems, Symmetries of simple lattices and role of GL(3, Z), The classification into Seven crystal systems and fourteen Bravais Lattices, Introduction to crystallographic concepts and their representations (last two topics to be detailed in a special lecture). Cauchy-Born hypothesis and Continuum thermoelastic theory of Crystalline Solids.
-
(V)Lecture 12, 13, 14 (5, 11 Feb): Martensitic phase transformation: three dimensional models: introduction to the study of equilibria.
-
(VI)Lecture (18, 19, 25, 26 Feb, 4, 18, 19 Mar): Martensitic phase transformation in one dimensional nonlinear elastic models: introduction to the study of equilibria, quasistatics, and dynamics (impact problem). Martensitic phase transformation in one dimensional nonlinear thermoelastic models: Introduction to the study of phase change dynamics and the concept of the driving force. Introduction to the study of equilibria.
-
(VII)Lecture (1 compensation lecture, 25, 26 Mar, 1, 2, 15, 16 Apr): Return to three dimensional thermoelasticity. Deformations with discontinuous deformation gradient and rank one tensors, Jump conditions in thermoelasticity. Martensitic phase transformation in three dimensional nonlinear thermoelastic models: introduction to the study of equilibria. Twinning and an example of cubic to tetragonal transformation. Energy minimization (energy wells) based approach for study of equilibria using calculus of variations and the presence of microstructure. Austenite-Martensite phase boundary. Shape memory effect.
-
(VIII)(optional topics, it time permits) Discussion on Ericksen-Pitteri neighbourhood, shock wave motion vs phase boundary motion, introduction to the study of quasistatics, and dynamics in three dimensional models.
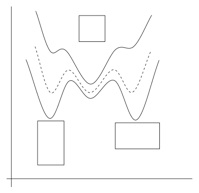




Tan, S. and H. Xu (1990) Observations on a CuAlNi single crystal, Cont. Mech. Thermodyn., 2, 241–244.
(a) from Klassen-Nekliudova (1964), courtesy of Kluwer Academic/Plenum Publishers; (b), (c) courtesy of C. Chu and R.D. James.


