ME 726

 

Announcements


...




Course details

Course No: ME 726

Instructor: Basant Lal Sharma

Department: Mechanical Engineering

Units: (L-T-P-D-U) 3-0-0-0-4

Schedule: LEC: M 15:00-16:00 FB370; W 16:00-17:00 FB370; Th 11:00-12:00 FB370;

Prerequisite: Strong background in linear algebra, real analysis and vector calculus (atleast the level of MTH101-102 with some maturity in the basic structure of mathematics) or permission of the instructor. Some knowledge of classical mechanics (dynamics) and/or differential geometry is a plus but it is not a prerequisite for this course.

Note: The course is offered and structured as science elective for undergraduate students and should also be available as departmental elective for post graduate (MTech/Dual Degree/PhD) students.




MY CONTACT

Email: bls at iitk.ac.in

Phone: 6173




Main Book

  1. 1.Arnold, V. I., 1989. Mathematical Methods of Classical Mechanics. Springer. Second edition. [Textbook: for part 1a only sections 18, 32--41, 44--48, for part 1b only sections 1--2, 13--17, 19].

  2. 2.Leimkuhler, B., Reich, S., 2004. Simulating Hamiltonian Dynamics. Cambridge University Press [Textbook: for part 2 chapters 1, 2, 4--7, 9].

  3. 3.Hairer, E., Lubich, C., Wanner, G., 2006. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations. Springer.

  4. 4.Goldstein, H., 1950. Classical Mechanics. Addison-Wesley Press.




Useful links

Wiki, Menger, Mathworld, Derivative, wiki, wiki

 

Course Summary


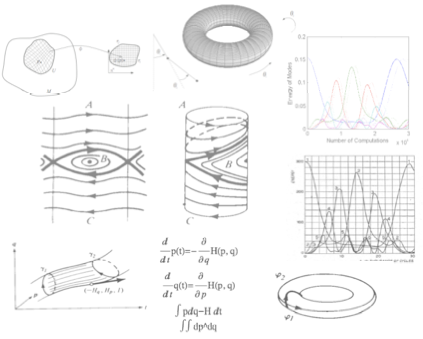
This course provides an introduction to the modern analytic and geometric modeling of Hamiltonian mechanics as well as an introduction to the numerical methods that preserve geometric properties of the Hamiltonian differential equations. One objective of the course is to expose the students to an abstract formulation of Hamiltonian mechanics (following V. I. Arnold) and its application in designing numerical (symplectic) algorithms for solving Hamiltonian problems. The latter is a special subset of algorithms belonging to the wider class of geometric integration algorithms and are widely used in molecular dynamics and celestial mechanics. Although the traditional numerical methods, such as Runge-Kutta schemes, have been hugely successful in science and engineering, the motivation for developing structure preserving algorithms for special classes of problems (such as Hamiltonian systems) exists, specially in astronomy, theoretical physics, mechanics, and numerical analyses of nonlinear systems etc.


The contents in more detail are as follows:

  1. •[Part 1] Some relevant definitions and results in the theory of differentiable manifolds, smooth vector fields, differential forms, (exterior) calculus (differentiation and integration using differential forms), differential equations and their associated flow maps, Symplectic manifolds.

  2. •[Part 2] Brief review of Hamiltonian mechanics (Lagrange's vs Hamilton's Equations), Canonical Transformation, Legendre Transformation, Symplectic Transformations, Some definitions and results in the theory of Continuous Groups for Symmetries and Conserved quantities, Poincare’-Cartan invariant, The Hamilton-Jacobi Partial Differential Equation. Integrable systems (simple examples).

  3. •[Part 3] Some basic notions of numerical algorithms (order conditions etc). Examples of Numerical methods, Symplectic Integrators, and Geometric integrators. Applications to simple problems in particle dynamics and a two body problem.

  4. •[Part 4] Some Symplectic Runge-Kutta Methods, Generating Function for Symplectic Runge-Kutta Methods and Symplectic Methods Based on it. Variational Integrators. Introduction to Hamiltonian Perturbation theory (if time permits). Discussion on some open problems in symplectic algorithms and a brief discussion on geometric numerical integration with some applications to mechanical systems.

Course FlyerME726_2011_files/handout.pdfshapeimage_7_link_0

Some information on Lectures


  1. (I)Lecture 1-2 (2): (Part 0: Introduction)

  2. (a) Overview of the course. Discussion on some applications, to mechanical systems, of geometric numerical integration.

  3. (b) Some applications of symplectic algorithms in understanding dynamics (of conservative systems). Discussion on constrained mechanical systems.

  4. (II)Lecture 3-12 (10): (Part 1: Differential Forms, Vector Fields and Manifolds)

  5. (a) Sets, Mappings, Structure of R, Differentiation and Integration in R, Diffeomorphisms in R.

  6. (b) Dual Vector Space, Exterior Forms in Rn (1-form, 2-form, k-form).

  7. (c) Exterior Product.

  8. (d) Differentiable Manifolds, Charts, Tangent Vectors, Vector fields.

  9. (e) Tangent Bundle, Cotangent bundle, Differential Forms.

  10. (f ) Behavior of Differential Forms Under Mappings.

  11. (g) Exterior Derivative.

  12. (h) Lie Derivative, Lie algebra of vector fields.

  13. (i) Chains (1-chain, 2-chain, k-chain), Boundary of Chains, Integration of differential forms, Stokes’ theorem.

  14. (j) Symplectic Structure in Rn , Symplectic Manifolds.

  15. (III)Lecture 13-23 (11): (Part 2: Hamiltonian mechanics)

  16. (a) Newtonian dynamics of n interacting particles (potential based interaction). Newton’s, Lagrange’s and Hamilton’s equations for n interacting particles. Legendre Transformation.

  17. (b) Configuration space and Phase space.

  18. (c) Hamiltonian function and vector fields, Lie algebra of Hamiltonians.

  19. (d) Differential equations and their associated flow maps, Phase flows.

  20. (e) Canonical Transformation.

  21. (f ) Symplectic Transformations, Symplectic maps and Hamiltonian flow maps.

  22. (g) Invariants.

  23. (h) Poincare’-Cartan invariant.

  24. (i) Some definitions and results in the theory of Continuous Groups for Symmetries and Conserved quantities.

  25. (j) The Hamilton-Jacobi Partial Differential Equation.

  26. (k) Integrable systems (simple examples).

  27. (IV)Lecture 24-30 (7): (Part 3: Examples of Numerical Algorithms)

  28. (a) Some basic notions of numerical algorithms (order conditions etc).

  29. (b) Examples of Numerical methods.

  30. (c) Symplectic Integrators and Geometric integrators.

  31. (d) Applications to simple problems in particle dynamics and a two body problem.

  32. (e) One-step methods, Numerical example. Higher-order methods, Numerical example.

  33. (f ) Runge-Kutta methods.

  34. (g) Forward v. backward error analysis.

  35. (V)Lecture 31-40 (10): (Part 4: Symplectic Algorithms)

  36. (a) Construction of symplectic methods by Hamiltonian splitting. Case studies.

  37. (b) Symplectic Runge-Kutta Methods (1).

  38. (c) Symplectic Runge-Kutta Methods (2).

  39. (d) Generating Function for Symplectic Runge-Kutta Methods (1).

  40. (e) Generating Function for Symplectic Runge-Kutta Methods (2).

  41. (f ) Symplectic Methods Based on Generating Functions.

  42. (g) Numerical experiments.

  43. (h) Variational Integrators.

  44. (i) Introduction to Hamiltonian Perturbation theory (if time permits).

  45. (j) Discussion on some open problems in symplectic algorithms.

Hamiltonian Mechanics and Symplectic Algorithms