Eddy viscosity
It follows a mixing hypothesis, corresponding to molecular transport in ideal gases
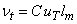 |
(10.2) |
where 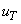 is the characteristic velocity scale of turbulence. The length scale is the characteristic velocity scale of turbulence. The length scale 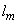 quantifies the turbulent transport or mixing process and is traditionally called the mixing length. The symbol C is the model constant. The coefficient C should be expected to depend on the flow but the ambition is to develop general models in which C has a single value. quantifies the turbulent transport or mixing process and is traditionally called the mixing length. The symbol C is the model constant. The coefficient C should be expected to depend on the flow but the ambition is to develop general models in which C has a single value.
The simplest choice of a model for the eddy viscosity is to set 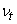 = constant. This approach works well for self similar jets and wakes. These flows are statistically two dimensional and fully developed. This entails turbulence to be both in internal equilibrium and in equilibrium with the mean flow. A more general approach for self-similar jets and wakes to set = constant. This approach works well for self similar jets and wakes. These flows are statistically two dimensional and fully developed. This entails turbulence to be both in internal equilibrium and in equilibrium with the mean flow. A more general approach for self-similar jets and wakes to set 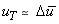 and and 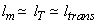 where where 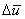 is a measure of transverse variation of the mean streamwise velocity and is a measure of transverse variation of the mean streamwise velocity and 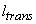 is the breadth of the jet and wake. is the breadth of the jet and wake.
The model for eddy viscosity 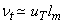 can be completed by modeling the velocity scale as can be completed by modeling the velocity scale as
 |
(10.3) |
This model for eddy viscosity and Reynolds stress is said to be “zero-equation” model. It does not require solution of a transport equation for the property of turbulence.
Generally, the characteristic velocity scale of the turbulence 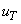 is estimated by is estimated by 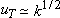
where
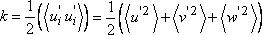 |
(10.4) |
is the kinetic energy of turbulence. The model for eddy viscosity and Reynolds stress then requires solution of k -equation. The mixing length can be modeled by  . The resulting k- l model is called “one equation” model of turbulence since it is based on a single transport equation, k -equation. . The resulting k- l model is called “one equation” model of turbulence since it is based on a single transport equation, k -equation.
In complex flows it is not possible to identify a single unique 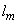 or or 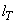 at every point in the flow. Many people use a modeled at every point in the flow. Many people use a modeled 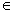 equation which also defines the length scale. This approach is known as “two-equation” model. The two-equation model is also known as k − equation which also defines the length scale. This approach is known as “two-equation” model. The two-equation model is also known as k − 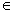 model, where model, where 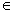 is the mean dissipation of the kinetic energy of turbulence. In this model the turbulent viscosity is estimated as is the mean dissipation of the kinetic energy of turbulence. In this model the turbulent viscosity is estimated as
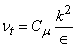 |
(10.5) |
This implies,
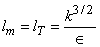 |
(10.6) |
Somewhat hand-waving, based on the eddy-viscosity model, with 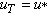 and and 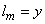 , one can write (for fully developed turbulence) , one can write (for fully developed turbulence)
 |
(10.7) |
where 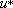 is the friction velocity, is the friction velocity, 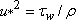 and and 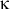 is von Karman constant, = 0.4. The log profile agrees with the measurement in the zone. is von Karman constant, = 0.4. The log profile agrees with the measurement in the zone.
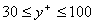 |
(10.8) |
|