Introduction

One can think of homogeneous turbulence as a complex tangle of vortex filaments, each acting as a “Biot-Savart source” in moving, distorting and straining all the filaments.

Figure 11.1

Vortex filaments of same orientation tend to collect leading to

• Creation of larger eddies

Counter balanced by the straining of filaments leading to

• Production of smaller eddies

The upper limit of size of the eddies is determined by the size of the apparatus. The lower limit is governed by viscosity and decreases by increasing average velocity.

Vorticity is the curl of velocity vector, i.e.,

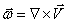(11.1)

In indicial notation

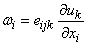(11.2)

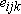is alternating tensor	= 1 if i,j,k are in cyclic order
	= -1 if i,j,k are in anticyclic order
	= 0 if any two indices are equal

Equation (11.2) can be written as:

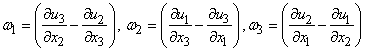(11.3)

It is possible to relate the defo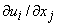rmation tensor with vorticity. The deformation tensor, 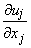can be split into a strain rate tensor and a rotation tensor in the following way

(11.4)

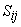, is the strain rate tensor (symmetric)

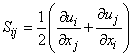(11.5)

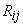, is called the rotation tensor and is a skew symmetric tensor

(11.6)

It is easy to show that

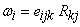(11.7)

and

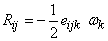(11.8)