Vorticity in Turbulent Flows
Reynolds decomposition of vorticity leads to
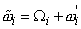 with with 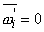 |
|
Substituting this in vorticity equation (13.1) and performing the averaging technique yields the following expression for steady mean flow
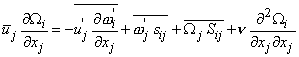 |
(13.5) |
In the above equation,
It is easy to prove that 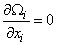 and and 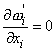 , i.e., both mean and fluctuating vorticity are divergence free. From these and the continuity equation, we can derive the following , i.e., both mean and fluctuating vorticity are divergence free. From these and the continuity equation, we can derive the following
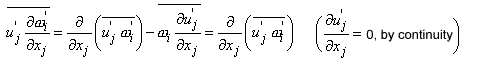 |
(13.6) |
and
RHS of (13.6) is analogous to Reynolds stress term in the momentum equation for mean flow. It is mean transport of 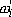 through its interaction with through its interaction with 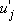 . Equation (13.7) accounts for the gain or loss of mean vorticity caused by stretching and rotation of vorticity components due to fluctuating strain rates. . Equation (13.7) accounts for the gain or loss of mean vorticity caused by stretching and rotation of vorticity components due to fluctuating strain rates.
The term  acts as a source or sink term in the equation for mean vorticity. This term is absent in a two-dimensional flow. If the flow is described by only acts as a source or sink term in the equation for mean vorticity. This term is absent in a two-dimensional flow. If the flow is described by only 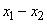 plane, then plane, then 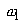 and and 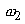 are trivial and only non-zero vorticity is are trivial and only non-zero vorticity is 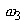 . The vortex stretching term in a two-dimensional flow field thus becomes . The vortex stretching term in a two-dimensional flow field thus becomes 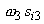 . In a two-dimensional flow field only . In a two-dimensional flow field only 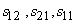 and and 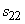 can be non-zero. Which tantamounts to can be non-zero. Which tantamounts to 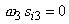 for a two-dimensional flow field. In conclusion it can be said that a two-dimensional flow is incapable of stretching a vortex. for a two-dimensional flow field. In conclusion it can be said that a two-dimensional flow is incapable of stretching a vortex.
An important use of the contraction cone in the upstream of a wind tunnel is that it reduces irregularities of the flow. The mechanism is as follows. In contraction cone, the angular velocity in the direction of stretching becomes greater. Vortex stretching brings about a change in eddy scales (decreases). At the exit of the contraction cone high energy eddies are obtained. These eddies keep changing the scale. A development section follows the contraction cone in which turbulence decays rapidly following the cascade mechanism of energy transfer. Finally, turbulence level goes down to a very low value at the entry point of the test section which follows the development section.
|