Kinetic energy of the mean flow
The equations of motion and continuity for turbulent flow, can be written as
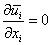
|
(14.1) |
 |
(14.2) |
where the stress tensor 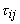 is given by is given by
In the above equation, p is the sum of static and turbulent pressures, the latter being (2/3)  . The quantity k is the kinetic energy of turbulence. For convenience, we use the symbol p for p / ρ in this section of the text. Density is thus absorbed in the pressure and the physical meaning of the equation remains unchanged. Thus . The quantity k is the kinetic energy of turbulence. For convenience, we use the symbol p for p / ρ in this section of the text. Density is thus absorbed in the pressure and the physical meaning of the equation remains unchanged. Thus
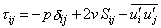 |
(14.3) |
The term  is the rate of strain of mean flow and can be expressed as is the rate of strain of mean flow and can be expressed as
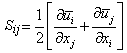 |
(14.4) |
The symbol 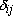 is the Kronecker-delta defined by is the Kronecker-delta defined by
If we multiply Equation (14.2) by 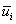 , we obtain the scalar equation , we obtain the scalar equation
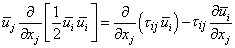 |
(14.5) |
By convection, repeated indices imply summation. Since by construction 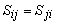 , it is clear that , it is clear that 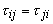 and Equation (14.5) may be written as and Equation (14.5) may be written as
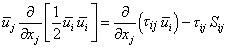 |
(14.6) |
The term (1/2) 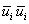 , signifies , signifies 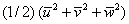 , the kinetic energy ( k ). Equation (14.6) can be interpreted as follows. The left hand side is the total derivative dk/dt representing the change in kinetic energy of affixed set of fluid particles as they move from are location to another. The right hand side is the total external work done on these particles by the combination of normal and tangential stresses. Hence, Equation (14.6) is a restatement of the mechanical energy equation in the absence of body forces (and hence potential energy).Equation (14.6) can also be looked upon as a transport equation. Noting that the volume integral. , the kinetic energy ( k ). Equation (14.6) can be interpreted as follows. The left hand side is the total derivative dk/dt representing the change in kinetic energy of affixed set of fluid particles as they move from are location to another. The right hand side is the total external work done on these particles by the combination of normal and tangential stresses. Hence, Equation (14.6) is a restatement of the mechanical energy equation in the absence of body forces (and hence potential energy).Equation (14.6) can also be looked upon as a transport equation. Noting that the volume integral.
one can interpret terms such as 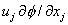 as transport terms carrying the quantity f out of a control surface with a velocity u . Hence, as transport terms carrying the quantity f out of a control surface with a velocity u . Hence, 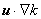 is a transport term of kinetic energy. From Equations (14.3) and (14.6) we get is a transport term of kinetic energy. From Equations (14.3) and (14.6) we get
We know that 
and
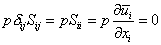 (from continuity) (from continuity) |
|
Hence we get the kinetic energy equation for time-averaged (base) flow as
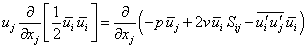 |
|
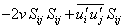 |
(14.7) |
Equation (14.7) is an expended form of the mechanical energy equation with the contributions of normal stresses, viscous stresses and fluctuations written explicitly. The left side is the transport term of the kinetic energy of the base flow. The first term on the right hand side of Equation (14.7) is pressure work while the second term corresponds to the mechanical work contribution associated with the viscous stresses . The third term is the mechanical work contribution of the turbulent stresses . The viscous dissipation is accounted for by the fourth term, and the fifth term signifies energy delivered by gradients in mean velocity 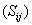 to turbulence.It may be mentioned that the viscous dissipation ( to turbulence.It may be mentioned that the viscous dissipation ( 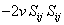 ) is a loss term to the kinetic energy budget, due to the negative sign. Similarly the fifth term is also negative (since ) is a loss term to the kinetic energy budget, due to the negative sign. Similarly the fifth term is also negative (since 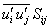 is non-zero and negative, if the overall velocity gradient is positive) signifying that turbulence drains energy from the base flow. The viscous dissipation referred here is related to the mean flow. It has the same sign as the energy delivered to turbulence by the base flow, almost everywhere in the flow field. is non-zero and negative, if the overall velocity gradient is positive) signifying that turbulence drains energy from the base flow. The viscous dissipation referred here is related to the mean flow. It has the same sign as the energy delivered to turbulence by the base flow, almost everywhere in the flow field.
|