Two-Equation Models

The family of two equation models are usually implemented as k- ε , and k- ω models. First let us introduce k- ε model.

k- ε Model

The turbulent viscosity , v_t in Equation (26.6), is computed from a velocity scale ( k ^1/2 ) and a length scale ( k^3/2 / ε ) which are predicted at each point in the flow via solution of the following transport equations for turbulent kinetic energy ( k ) and its dissipation rate ( ε ):

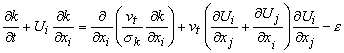	(27.8)
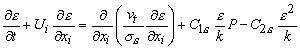	(27.9)

where P is the generation of k and is given by

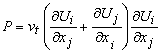(27.10)

The turbulent viscosity is then related to k and ε by the expression

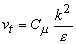(27.11)

The coefficients C_μ , C_1ε , C_2ε , σ_k and σ_ε are constants which have the following empirically derived values

C_μ = 0.09, C _1ε= 1.44, C _2ε= 1.92, σ_k = 1.0, σ_ε= 1.3

This is the central concept for a family of two equation of models (Jones and Launder, 1972; Launder and Spalding, 1974) where the equation for turbulent kinetic energy determines the velocity scale. The two equation models are quite successful and have become very popular for engineering applications. With only little modification, they are able to simulate a large variety of flows with reasonably good degree of accuracy.

Following the philosophy of momentum equation, the thermal energy or species concentration conservation equation can be written as

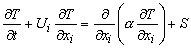(27.12)

where T is temperature and S is the source term. Reynolds decomposition suggests:

and the time averaged equation becomes

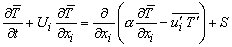(27.13)

In direct analogy to the turbulent momentum transport, the turbulent heat or mass transport is often assumed to be related to the gradient of the transported quantity

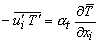(27.14)

where α_t is the turbulent diffusivity of heat or mass . Like eddy viscosity, α_t is not a fluid property but depends on the state of the turbulence . In fact, the Reynolds analogy between heat and momentum transport suggests

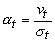(27.15)

The quantity σ_t is called turbulent Prandtl or Schmidt number.

Experiments have shown that σ_t varies very little across any flow. Its variation from flow to flow is also small. Therefore many models make use of σ_t as a constant. For the flow of air, a value of 0.9 may be taken. It should be pointed out that buoyancy and streamline curvature affect σ_t .