For a developed turbulent flow, in the near wall region, inertial effects are insignificant and we can write eqn. (9.2) as
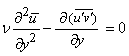 |
(9.3) |
which may be integrated as
 constant constant |
(9.4) |
As we know, the fluctuating components do not exist near the wall, the shear stress on the wall is purely viscous.
It follows
 |
(9.5) |
The wall shear stress is estimated as in Couette flow by
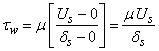 |
(9.6) |
where  is the fluid velocity at the edge of sublayer. A friction velocity or viscous velocity is defined as is the fluid velocity at the edge of sublayer. A friction velocity or viscous velocity is defined as
 |
(9.7) |
It has been confirmed experimentally that the turbulent intensity distributions are scaled with 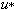 . For example, maximum value of . For example, maximum value of 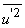 is always about 8 is always about 8 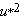 . The relationship between . The relationship between 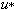 and and  can be determined from (9.6) and (9.7) as can be determined from (9.6) and (9.7) as
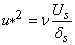 |
(9.7) |
Let us assume 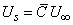 . We can now write . We can now write
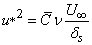 where where 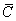 is a proportionality constant is a proportionality constant
or,
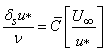 |
(9.8) |
A non-dimensional coordinate may be defined as
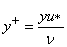 |
(9.8) |
- The thickness of laminar sublayer,
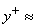 5 5
- Turbulent effect starts in the zone,
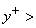 5 5
- Laminar and turbulent motions co exist, 5 <
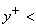 70 70
- Turbulent core,
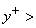 70 70
|