Topology? Transport?

Topology in physics is a breathtaking but quite familiar concept used extensively in condensed matter, quantum field theory and physical cosmology among many other fields. You may already be familiar with Aharonov-Bohm effect, which is a consequence of appearance of geometric phases in condensed matter. You may also be excited about the fact that an Indian, S. Pancharatnam was among the first to describe such geometric effects. Now, the breakthrough came, in the form of quantum-Hall effect, where the consequence of such geometric phase was a dramatic quantization of Hall coefficients. Klaus von Klitzing won the Nobel prize in 1985 for the experimental discovery of the effect. Robert B. Laughlin, Horst Störmer and Daniel Chee Tsui won the 1998 Nobel prize with the discovery of "fractional" quantum hall systems, which is the culmination of efforts in understanding topology in interacting systems.

Graphene opened up immense possibilities in early 2000 as an excellent test bed for quantum system in the world of two dimensions. Eluding physics, like relativistic motions of electrons, was achievable and a technological breakthrough was evident. Soon enough a number of other "interesting" objects were discovered, like quantum spin-Hall systems opening up an really extensive field of research "topological insulators." Andre Geim and Konstantin Novoselov won the 2010 Nobel prize for experimental realization of graphene.

In the mean time quantum computing is starting to enter a mature phase where the dream of realizing a quantum computer is not looking far off. Topological systems are paving the path for such realizations. As an example, Majorana fermions in topological superconductor may act as an excellent candidate for quantum information processing. J. Michael Kosterlitz, Duncan Haldane and David J. Thouless won the 2016 Nobel prize for providing us with the understanding and opening up the possibilities of topological phase transitions in physics. Such theoretical endeavor is also met with many progress in the experimental front, such as the development of cold atom experiments. The race between the theorists and experimentalists is getting close.

So, what is topology? Topological invariants are something that characterizes closed surfaces (compact manifolds!). As an example, we may smoothly deform one surface into another without filling up any holes they have. All the surfaces which can be deformed into each other with such restrictions, we'll say, belong to the same topological class. A well known example is that a cup and a donut belong to the same class, which is a class different from the class where a football would fall into. In mathematical sense, the integral of Gaussian curvature $k_g$ over the closed surface produces $$\oint_{\rm surface} k_g \frac{dS}{2\pi} = 2-2g,$$ where $g$ is the genus or the number of holes in the surface, which characterizes the topology of the surface.

Such closed surfaces in true sense is what a Brillouin zone for the case of lattices. And, there is something called the Berry curvature that can be defined in the Brillouin zone. And it turns out that, the integral of the Berry curvature (in two dimensions) is something related to the Hall conductance $\sigma_{xy}$ of a system $$ \oint_{\rm Brillouin~zone} F_{xy} \frac{dk_x dk_y}{2\pi} = \sigma_{xy} $$ This is where the topology of the system comes into place. Because this integral needs to be an integer (times the unit of quantum conductance). This integer Hall effect is called the quantum Hall effect.

Quantum transport in a very powerful tool in understanding basic rules and properties of quantum systems. In recent times, quantum transport, both theoretically and experimentally is being used extensively in probing and understanding the so called "topological systems" in condensed matter. Along with understanding and utilization of various neighboring fields of research, like mesoscopic as well as non-equilibrium physics, this creates a field of research that you may call as "topology and transport in quantum systems".

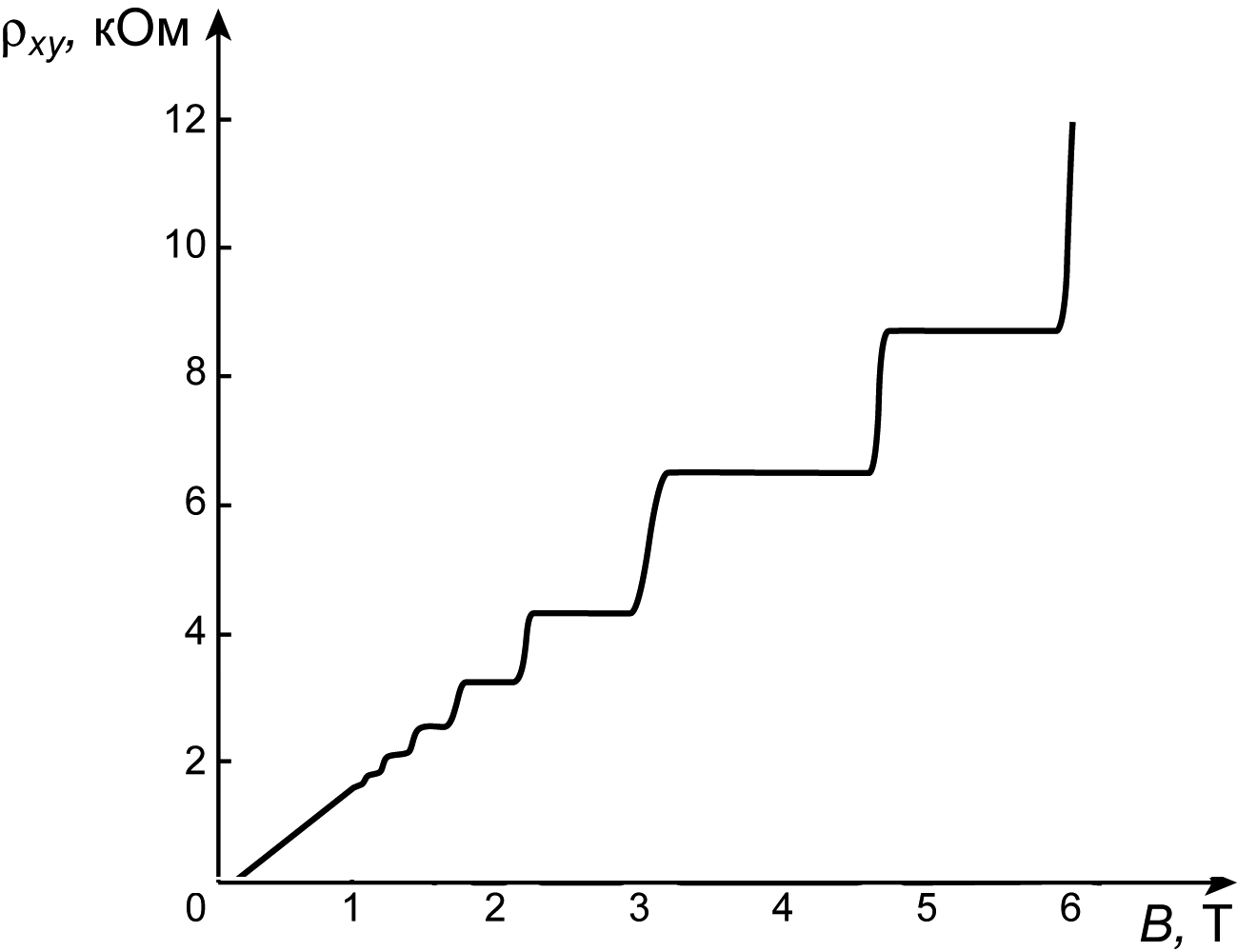
If we apply this, for example, to the quantum Hall effect, we find that the resistivity $\rho_{xy} = 1/\sigma_{xy}$, we get only values $\propto 1/$integers. This was precisely what has been observed experimentally!

Just like quantum Hall effect, in general, the signatures of 'non-trivial' topology is often expected to be found in transport properties of the system.

Research.

Our current research focus is to characterize topological phases (and phase transitions), both in equilibrium and in non-equilibrium, understand their behavior when it comes to quantum transport and to propose setups which may lead to futuristic technologies. Interaction effects, such as disorder, electromagnetic radiation, electron-phonon and electron-electron interactions are crucial ingredient for the rich physics such systems may present to us. A number of analytical and numerical methods, such as scattering matrix, equilibrium and non-equilibrium Green's function method are at our disposal.

Topological aspects in Floquet systems

Topological aspects in non-equilibrium is a rather new field of research. Here we deal with systems that are periodic in time. Such systems are often called Floquet systems, in the name of the French mathematician Gaston Floquet, who discovered many important properties of differential equations which are periodic in certain parameter. In our context what a periodic time does, is that, it gives us another compact (closed) direction to integrate some "curvatures" $$ \oint F(k_x,k_y,t) \frac{dk_xdk_ydt}{2\pi} = {\rm some~integer}$$ Of course, it is of immense difficulty to find a physically observable curvature that we can integrate on. But, fortunately, it turns out that is possible. This led into the the development of the Floquet topological systems in last few years, both theoretically and experimentally.

Lets set our language first. In time periodic system, i.e, for a Hamiltonian $H(t+T)=H(t)$, the energy is not anymore a conserved quantity. Rather, we have something called "quasienergy" that takes the place of energy. This follows from the synergy between time periodic and space periodic (or, lattice!) systems, where we had Bloch momentum in place of momentum. These quasienergies, as you rightly may guess, depend a lot on the frequency of drive. Here I uploaded a short video, how the quasienergy bands of something like graphene may drastically change with the frequency of an applied circularly polarized light. This gives, firstly, many quantum phase transitions and secondly a great control over the band structure.

We have investigated such "topological" phase transitions theoretically, and we could characterize such phases with different topological invariants.

Next, we proposed a number of interesting scenarios that can be achieved in this systems which are non-trivial and it is possible that some of the physics is never possible in an equilibrium system. For example, we can arrive in a situation where disorder can lead to enhanced transport.

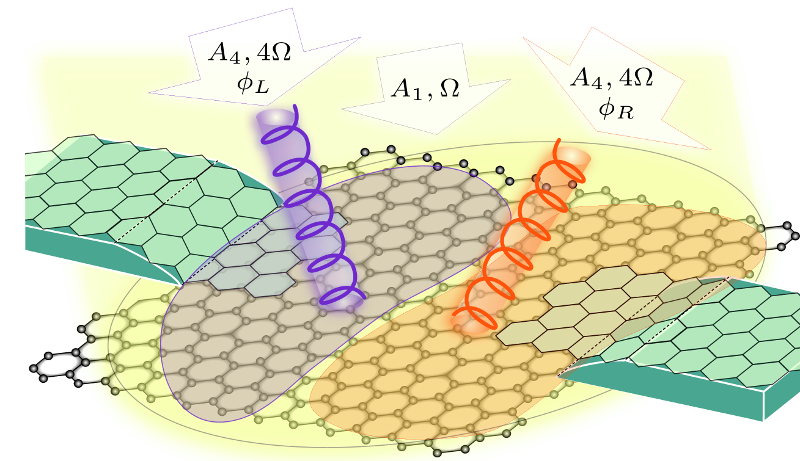
One can also device systems that can lead to futuristic technologies. We proposed a system, which is the complex picture you see in the left, where a new form of electronics, called "valleytronics" can be utilized. I'll skip the details here, of course!

Then there are even more complex ideas. Something like Floquet Majorana fermions. These are candidates for quantum information processing. But before one goes into fighting the challenges of using them, we first need to know that how can they be produced in a lab and be detected successfully. In a series of works we managed to discuss both of these aspects.

Although graphene is special, there are many other systems, where periodic drive can lead to many interesting new physics. We have studied one example, silicene in some details. This could be an interesting area for further research in the future.

Transport in emergent topological systems, such as Weyl semimetal

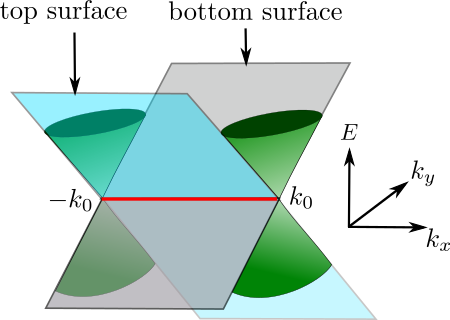
Weyl semimetals are another very recent topic which generated tremendous enthusiasm among theorists and experimentalists alike. In graphene the electrons move like relativistic particles, following something called the Dirac equation. The problem is, these Dirac equations can easily become massive (that means one needs an finite amount of energy to excite some particles). This gets resolved if we have a Weyl system in three dimensions. But such Weyl nodes (momentum near which we have low energy excitations) can always come in pairs. Once they join each other, they form a Dirac node! What is more is that, they host a couple of surface states that join them in the momentum space. Something like what is in the figure.

First of all, we need to know that such Weyl nodes are present in a system. Among many others, we proposed a system that involves creating a Josephson junction with such materials. We also proposed how to tune the system parameters with precision by applying a polarized light on the sample. A number of related projects are on their way.

Other stuffs

People.

Group postdocs and students: