Functions of Several Variables
The Euclidean distance between two points x = (x1, x2, … , xn) and x = (y1, y2, … , yn) in
Rn is defined byP
x-yP º d(x,y) = [S1£ j£ n (xj - yj)2]1/2.An open ball or a ball in Rn with center a and radius r is defined by B(a, r) = {x : Px-aP < r}. B[a, r] = {x : Px-aP £ r} is the corresponding closed ball. A ball is also called a sphere and one talks about a closed sphere and an open sphere. In geometry a sphere is used both for the surface S(a, r) = {x : Px-aP = r} of the sphere and the closed sphere B[a, r]. We will use the word sphere or a ball to mean an open sphere, unless otherwise stated. A subset of Rn is called open if it contains a sphere of a positive radius about each of its points x. A subset is called closed if its complement is open.
The treatment of functions of two and three variables generalizes, mutatis mutandis, for several variables. Hence mostly we shall consider functions of two variables x, y (i.e., defined on subsets of plane), and, because of everyday applications those of three variables x, y, z (i.e., defined on subsets of space). The variables x, y, z themselves could be functions of another variable t which would normally denote time.
Of the first order partial derivatives fx, fy, fz, of the function f(x, y, z) of three variables x, y and z, e.g., fx at the point (x, y, z) is defined by
(¶ f/¶ x)(x, y, z) º fx(x, y, z) = limh® 0 [f(x+h, y, z)-f(x, y, z)]/h.
Note that one would write fx(1.0, 2.0, 3.1) to denote the partial derivative with respect to x, the first variable, at the point (1.0, 2.0, 3.1). Thus the naming of the variables and their order is implicitly assumed.
One could continue defining partial derivatives of partial derivatives which would be partial derivatives of higher order. Thus there are three first order partial derivatives of f(x, y, z) viz., fx = ¶f/¶x, fy = ¶f/¶y, and, fz = ¶f/¶z, nine second order partial derivatives: fxx º ¶2f/¶x2 º ¶2f/¶x¶x º (¶/¶x)(¶/¶x)f, fxy º ¶2f/¶x¶y º (¶/¶y) (¶/¶x)f º (¶/¶y) (¶f/¶x) = (fx)y, … , and so on.
A function f(x, y) is said to be differentiable at a point (a, b) if there exist constants A and B such that
f(a+h, b+k) - f(a, b) = Ah + Bk + o(|h| + |k|), as |h| + |k| ® 0.
Differentiability at a point implies the continuity of the function at the point, as well as the existence of the first order partial derivatives of the function at the point. The existence of the first order partial derivatives at a point, however, does not imply even the continuity of the function at the point, as follows from the example at (0, 0) of
![]() .
.
Calculus of Functions of Several Variables
Theorem. If the first order partial derivatives fx(x, y) and fy(x, y) of the function f(x, y) exist in a neighborhood of a point (a, b) and are bounded there, then f(x, y) is continuous at (a, b).
Proof
: The existence of partial derivatives in a neighborhood of (a, b) implies the continuity of f(x, y) on horizontal and vertical lines in a neighborhood of (a, b). Now, by the mean value theorem for functions of one variable, there exist q 1, q 2 Î (0, 1) such that f(x, y) – f(a, b) = [f(x, y) – f(a, y)] + [f(a, y) - f(a, b)] = fx(a+q 1(x-a), y)(x-a)+fy(a, b+q 2(y-b))(y-b) ® 0, as (x, y) ® (a, b). #Chain Rule. If w = w(x) and x = x(t) then dw/dt = (dw/dx)(dx/dt) provided the right hand side is meaningful.
Proof
: Note that w = w(x) = w(x(t)), Dx = Dx(t) = x(t+Dt)-D(x), etc. so that Dw/Dt = [w(x(t+Dt))-w(x(t))]/Dt =(Dw/Dx)(Dx/Dt). Passing to the limit as Dt ® 0, Dx ® 0 and we have the result. #Chain Rule for Functions of Several Variables. Let w = w(x, y) and x = x(t), y = y(t). If (i) the partial derivatives ¶ w/¶ x, ¶ w/¶ y exist in a neighborhood of (x, y) = (x(t), y(t)) and are continuous at (x, y) and, (ii) x, y are differentiable at the point t, then
dw/dt = (¶w/¶x)(dx/dt) + (¶w/¶y)(dy/dt).
Proof
: By the mean value theorem for functions of one variable,D
w/Dt = (w(x+Dx, y+Dy)–w(x, y))/Dt= [(w(x+
Dx, y+Dy)–w(x, y+Dy)/Dx][Dx/Dt] + [(w(x, y+Dy)–w(x, y)/Dy][Dy/Dt]= [
¶ w(x+q1Dx, y+Dy)/¶x][Dx/Dt] + [¶w(x, y+q2Dy)/¶x][Dy/Dt],where 0 <
q 1, q 2 <1. Passing to the limit as Dt ® 0, Dx, Dy ® 0, and the result follows. #The chain rule obviously extends to a function f
º f(x) º f(x1, … , xn) of n-variables n ³ 2, in which the partial derivatives are assumed to exist in a neighborhood of x = (x1, … , xn) and be continuous at the point x, with the vector variable x(t) being a differentiable functions of t:df/dt = S 1£ i£ n (¶f/¶xi)dxi/dt.
Theorem (Interchange of Order of Partial Differentiation). Let the partial derivatives fxy and fyx of the function f(x, y) exist in a neighborhood of (a, b) and be continuous at the point (a, b). Then, fxy(a, b) = fyx(a, b).
Proof
: Let g(x, y, a, b) = f(x, y) - f(x, b) – f(a, y) + f(a, b). By the mean value theorem used for the variable x, for some q1 Î (0, 1),g(x, y, a, b) = [f(x, y)-f(x, b)] – [f(a, y)-f(a, b)] = [fx(a+
q1(x-a), y) - fx(a+q1(x-a), b)](x-a)= fxy(a+q1(x-a), b+q2(y-b))(x-a)(y-b),
for some q2 Î (0, 1), by mean value theorem used for the variable y.
Next, by the mean value theorem used for the variable y, for some q3 Î (0, 1),
g(x, y, a, b) = [f(x, y)-f(a, y)] – [f(x, b)-f(a, b)] = [fy(x, b+q3(y-b)) - fy(a, b+q3(y-b))](x-b)
= fyx(a+q4(x-a), b+q3(y-b))(x-a)(y-b),
for some q4 Î (0, 1), by mean value theorem used for the variable x.
Hence, by the continuity of the partial derivatives fxy and fyx at the point (a, b),
fxy(a, b) = lim(x, y)® (a, b) g(x, y, a, b)[(x-a)(y-b)]-1 = fyx(a, b). #
Mean Value Theorem for Functions of Several Variables. Let f(x, y) be continuous on the line segment joining the points (a, b) and (a+h, b+k) and let the first order partial derivatives of f(x, y) exist in a neighborhood of the interior of the line segment joining (a, b) and (a+h, b+k) and be continuous at all interior points of the segment. Then, for some q Î (0, 1),
f(a+h, b+k) – f(a, b) = hfx(a+qh, b+qk) + kfy(a+qh, b+qk).
Proof
: Define g(t) = f(a+th, b+tk). Since the partial derivatives fx and fy exist in a neighborhood of the interior of the line segment and are continuous at each point of the interior of the segment, the derivatives of g(t) at the interior points of the line segment could be evaluated by the chain rule. By the mean value theorem for functions of one variable for a q Î (0, 1), f(a+h, b+k)–f(a, b) = g(1)-g(0) = g¢(q ) = hfx(a+qh, b+qk)+kfy(a+qh, b+qk). #Taylor’s Expansion with Remainder for Functions of Several Variables. Let f(x, y) be continuous on the line segment joining the points (a, b) and (a+h, b+k). Let the n-th order partial derivatives of f(x, y) exist in a neighborhood of the line segment joining (a, b) and (a+h, b+k) and be continuous at all points of the segment. Then, for some q Î (0, 1),
f(a+h, b+k) = f(a, b)+S1£ k£ n-1 (h¶/¶x+k¶/¶y)jf(a, b)/j! + (h¶/¶x+k¶/¶y)nf(a+qh, b+qk)/n!.
Proof
: Note that the continuity of the n-th order partial derivatives at all points of the segment imply their boundedness in the neighborhood of each point of the segment, which in turn implies the continuity of the (n-1)-th and all lower order partial derivatives at all points of the segment. Hence, for the function g(t) = f(a+th, b+tk) by the chain rule for functions of several variables, g(j)(t) = (h¶/¶x+k¶/¶y)jf(a+th, b+tk), t Î [0, 1]. The result follows from the Taylor’s expansion g(1) = g(0) + S 1£ j£ n-1 (j!)-1g(j)(0) + (n!)-1g(n)(q), for some q Î (0, 1). #Taylor’s Approximation for Functions of Several Variables. Let the n-th order partial derivatives of f(x, y) exist in a neighborhood of (a, b) and be continuous at (a, b). Then,
f(a+h, b+k) = f(a, b)+S 1£ k£ n (h¶/¶x+k¶/¶y)jf(a, b)/j! + o(|h|+|k|)n, as (|h|+|k|) ® 0.
Proof
: Let H = h/(|h|+|k|), K = k/(|h|+|k|), g(t) = f(a+tH, b+tK). As g¢ (0) = Hfx(a, b) + Kfy(a, b), g(j)(0) = (H¶/¶x + K¶/¶y)jf(a, b), 1 £ j £ n. By the Taylor’s expansion g(t) = g(0) + S1£j£n g(j)(0)tj/j! + o(t)n, t ® 0. Hence, putting t = |h|+|k| in this relation we have f(a+h, b+k) = f(a, b) + S 1£ j£ n (tH¶/¶x + tK¶/¶y)jf(a, b)/j! + o(|h|+|k|)n = f(a, b) + S 1£ j£ n (h¶/¶x + k¶/¶y)jf(a, b)/j! + o(|h|+|k|)n, as (|h|+|k|) ® 0. #
Change of Variables in Double Integrals
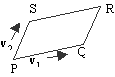
Area of a Parallelogram
Consider a parallelogram PQRS in the plane with the coordiantes P(x, y), Q(x+p, y+q), R(x+p+r, y+q+s), S(x+r, y+s). The vectors represented by the concurrent sides PQ and PS are v1 = pi + qj and v2 = ri + sj, respectively. If
q is the angle between the vectors v1 and v2, |v2| |sin q | is the hight of the parallelogram with |v1| the base, so thatArea of Parallelogram = |v1
´ v2| = |v1||v2| |sin q | = | | = |
| = |Theorem (Change of variables in Double Integrals). Let D¢ be a domain in the uv-plane. Let x = x(u, v), y = y(u, v) be a smooth 1-1 map of D¢ onto a region D in the xy-plane. Then
ò
ò D f(x,y)dxdy = ò ò D¢ f(x(u,v),y(u,v)|det J|dudv,where the Jacobian J of the transformation is given by:J = ¶(x,y)/¶(u,v) = ![]() .
.
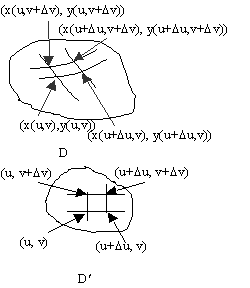
Proof
: Let us use a rectangular mesh in D¢ . The rectangular area element DA¢ defined by the points {P¢(u, v), Q¢(u+Du, v), R¢(u+Du, v+Dv), S¢ (u, v+Dv)} in D¢ maps approximately into a parallelogram area D A defined by the points {P(x, y), Q(x + (¶x/¶u)Du, y + (¶y/¶u)Du), R(x + (¶x/¶u)Du + (¶x/¶v)Dv, y + (¶y/¶u)Du + (¶y/¶v)Dv), S(x + (¶x/¶v)Dv, y + ¶y/¶v)Dv)} in D. This is because of the first order approximationsx(u+
Du, v+Dv) @ x(u, v) + (¶x/¶u)Du+(¶x/¶v)Dv,y(u+
Du, v+Dv) @ y(u, v) + (¶y/¶u)Du+(¶y/¶v)Dv,for all sufficiently small
Du, Dv. Hence the rectangular subdivision in D¢ induces a subdivision in D consisting of approximate parallelograms.Note that
DA¢ = DuDv and DA = |det J|DuDv. Hence the Riemann sumS
f(x(u, v), y(u, v)) |det J|DuDv ® òòD f(x, y))dxdy.But this Riemann sum is also an approximation to the integral ò òD¢ f(x(u, v), y(u, v)) |det J| dudv. Hence, we must have
òò
D f(x, y))dxdy = ò òD¢ f(x(u, v), y(u, v)) |det J| dudv.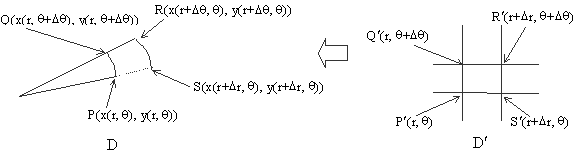
Example. For the cartesian to polar transformation x = r cos q , y = r sin q , J = ¶(x,y)/¶(r,q) = ![]() , |det J| = r, and therefore if a region D¢ in the (r, q ) plane is 1-1 mapped onto the region D in the (x, y) plane,
, |det J| = r, and therefore if a region D¢ in the (r, q ) plane is 1-1 mapped onto the region D in the (x, y) plane,
òò
D f(x,y)dxdy = òò D¢ f(r cos q, r sin q) rdrdq . (Polar coordinates)Thus, the area of a circle D of radius R with center at (0, 0) in the xy-plane is mapped on to the rectangle D
¢ = [0, R]´[0, 2p ] in the rq -plane. Accordingly the area of the circle òòD dxdy = òòD¢ rdrdq = ò(0,2p ) [ò(0,R) rdr]dq = (R2/2)2p = pR2. Note that the evaluation òòD dxdy = ò(-R,R) [ò(-Ö (R2-x2),Ö (R2-x2)) dy]dx = ò(-1,1) 2Ö(R2-x2)dx = (putting x = R sin q ) ò(-p/2,p /2) 2Rcos2q Rdq = R2 ò(-p/2,p/2) [1 + cos 2q ] dq = R2[q + (sin 2q)/2]| (-p/2,p/2) = pR2, is much more complicated.Change of Variables in Triple Integrals
Volume of a Parallelopiped
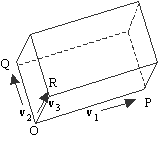
Consider parallelopiped in the 3-D space with the three concurrent edge vectors OP, OQ, OR given by v1 = x1i + y1j + z1k, v2 = x2i + y2j + z2k, v3 = x3i + y3j + z3k. Its volume is the magnitude of the scalar triple product given by
Volume of Parallelopiped = |[v1, v2, v3]| = |(v1
´v2)×v3| = |det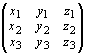 |.
|.
Note that v1´v2 relates to the base area, and the subsequent dot product multiplies the base area with the hight of the parallelogram along with a sign which is positive if the angle between v1´ v2 is acute, negative if the angle is obtuse. If v3 lies in the plane of v1, v2 the area, indeed, is zero.
Theorem (Change of variables in Triple Integrals). Let the change of variables
x = x(u, v, w), y = y(u, v, w) , z = z(u, v, w)
map a region D¢ in the uvw-space 1-1 onto a region D in the xyz-space. Then,
òò
D f(x, y)dxdydz = òòD¢ f(x(u, v), y(u, v)|det J|dudvdw,where the Jacobian J of the transformation is given by:
J = ¶(x,y,z)/¶(u,v,w) = 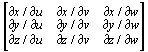 .
.
Proof: Consider a subdivision of D¢ through rectangular parallelopipeds with edges pararallel to to coordinate axes in the uvw-space. Let the coordinates of the vertices O, P, Q, R associated with the concurrent edges OP, OQ, OR of a rectangular parallelopiped volume element be (u, v, w), (u+Du, v, w), (u, v+Dv, w), (u, v, w+Dw). The change of variable maps this volume element into an approximate parallelopiped with the associated concurrent edge vectors as: v1 = (¶x/¶u)Du i + (¶y/¶u)Du j + (¶z/¶u)Du k, v2 = (¶x/¶v)Dv i + (¶y/¶v)Dv j + (¶z/¶v)Dv k, v3 = (¶x/¶w)Dw i + (¶y/¶w)Dw j + (¶z/¶w)Dw k, which therefore has approximate volume as DV = |det J|DuDvDw. Thus the Riemann sum S f(x, y, z) |det J|DuDvDw ® òòòD f(x, y, z)dxdydz. As the sum is also a Riemann sum in R¢ associated with the integral òòòD¢ f(x(u, v, w), y(u, v, w), z(u, v, w))|det J|dudvdw, by the convergence of the Riemann sums to the associated integrals, we have òòòD f(x, y, z)dxdydz = òòòD¢ f(x(u, v, w), y(u, v, w), z(u, v, w)) |det J| dudvdw, which is the required change of variable formula. #
Example
. The transformation from the cartesian coordinates (x, y, z) to spherical coordinates (r, q, f) is given by: x(r, q, f) = r cos q sin f, y(r, q , f) = r sin q sin f , z(r, q , f) = r cos f , r Î [0, ¥), q Î [0, 2p), f Î [0, p ]. The Jacobian of the transformation is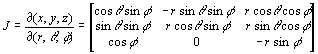
so that, det J = r2 [cos
f (-sin2q sinf cosf - cos2q sinf cosf) – sinf (cos2q sin2f + sin2q sin2f)] = - r2 sin f .The negative sign signifies that the infinitesimal vector triad forms a left handed system. Since, |det J|= r2 sin
f,òòò
R f(x,y,z)dxdydz = òòòR¢ f(rcosqsinf, rsinqsinf, rcosf) r2sinfdrdqdf, (Spherical)where the transformation maps the region R
¢ in the sphereical system to the region R in the cartesian system.The transformation from the cartesian (x, y, z) to cylindrical coordinates (r,
q, z) consists of x(r, q) = x(r, q, z) = r cos q, y(r, q) = y(r, q, z) = r sin q, z(r, q, z) = z, in which case we similarly have det J = r, so thatòòò
R f(x, y, z)dxdydz = òòòR¢ f(rcosq, rsinq, z) rdrdqdz. (Cylindrical)
The Gradient and the Directional Derivative
Let f = f(x, y, z)
º f(xi + yj + zk) º f(P) , be a scalar function. Its directional derivative at the point P = P(x, y, z) in the direction of a vector b (written as ¶f/¶s, or Dbf, or ¶ f/¶ u, where u = b/|b|) is defined by¶
f/¶s = lims® 0 [f((Q)-f(P)]/swhere s is the signed distance from P to Q and Q is such that an arrow from P to Q equals the vector su = sb/|b|. Writing v = xi + yj + zk, (i, j, k being the standard unit vectors) we have, by mean value theorem
¶
f/¶s = lims®0 [f(v+su)–f(v)]/s = lims®0 [f(v+su)–f(v)]/s = (¶f/¶x)u1 + (¶f/¶y)u2 + (¶f/¶z)u3, = Ñf×u = Ñf×(b/|b|),where
Ñ , the gradient operator is given bygrad = Ñ = i¶/¶x + j¶/¶y + k¶/¶z,
with its action given by
grad f º Ñf = (¶f/¶x)i + (¶f/¶y)j + (¶f/¶z)k.
Since
¶
f/¶s = |Ñf| cos g ,where cos
g denotes the direction cosine between Ñf and b, i.e., g is the angle between the gradient and the direction vector b, the directional derivative is maximum in the direction of the gradient and the maximum value is the magnitude of the gradient. Since of the maximum rate of change and its direction depends on the function only the gradient Ñ f is independent of the choice of the Cartesian coordinate system in the space, i.e., the origin of the coordinate system and the choice of the orthogonal x, y, z directions.The 3-D Space
R
= (-¥, ¥) - the real line.R
3 = {(x, y, z) : x, y, z Î R} - the 3-D space.x, y, z - the space variables representing the coordinates of a point.
i, j, k – the standard unit vectors in the x, y, and z directions.
The operator
Ñx, y, z - the space variables
Ñ
= i¶/¶x + j¶/¶y + k¶/¶yThe operator
Ñ is called the operator del.Gradient
f
º f(x,y,z) - a scalar function in R 3 of the variables x, y, z.grad f
º Ñf = (i¶/¶x + j¶/¶y + k¶/¶y)f(x, y, z) = i¶f/¶x + j¶f/¶y + k¶f/¶z.The gradient
Ñf of f(x, y, z) is a vector.Divergence
F
(x, y, z) º if1(x, y, z) + jf2(x, y, z) +kf3(x, y, z) - a vector function in R3 of the variables x, y, z.div F º Ñ×F = (i¶/¶x + j¶/¶y + k¶/¶y)× (if1 + jf2 +kf3) = ¶f1/¶x + ¶f2/¶y + ¶f3/¶z.
The divergence Ñ×F of F(x, y, z) is a scalar function of x, y, z.
Curl
F(x, y, z)
º if1(x, y, z) + jf2(x, y, z) + kf3(x, y, z) - a vector function in R3 of the variables x, y, z.curl F º Ñ ´ F = (i¶/¶x + j¶/¶y + k¶/¶z)´(if1 + jf2 +kf3) = i(¶f3/¶y - ¶f2/¶z) + j(¶f1/¶z - ¶f3/¶x) + k(¶f2/¶x - ¶f1/¶y)
= 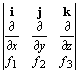 .
.
Line Integral
Let C = {r(t) : a
£ t £ b} be a rectifiable space curve, i.e., S 1£ i£ n |r(ti) - r(ti-1)| ® L, n ® ¥ , irrespectively of the subdivision a = t0 < t1 < … < tn = b, so long as the maximum subdivision length max0£ i£ n | ti - ti-1| ® 0. The line integral ò C fds, (s denoting the arc length along C, and f º f(r(t)) º f(x(t), y(t), z(t)) º f(x, y, z)), is defined (in the Riemann sense) asò
C fds = limn®¥ S1£ i£ n f(r(ti))|r(ti) - r(ti-1)|,where ti-1
£ ti £ ti is an arbitrary point, provided limits of all such sums exist and are equal. The line integral of the function [f(x, y, z)dx/ds + g(x, y, z)dy/ds + h(x, y, z)dz/ds], is simply written as òC (fdx + gdy + hdz). Note that òC fds = ò(a,b) f(x(t), y(t), z(t))|r¢(t)|dt = ò(a,b) f(x(t), y(t), z(t))(ds/dt)dt = ò(0,L) f(x(s), y(s), z(s))ds, andò
C (fdx+gdy+hdz) = ò(0,L) (fdx/dt+gdy/dt+hdz/dt)(dt/ds)ds = ò(a,b) (fdx/dt+gdy/dt+hdz/dt)dt.A space curve is called smooth if it possesses a continuous unit tangent at each of its points. The smoothness requirement of a space curve r = r(t) is equivalent to r(t) being a continuously differentiable function of t.
If v is a vector function, the integral
òC v×dr is defined asò
C v×dr = òC (v1dx + v2dy + v3dz).Surface Integral
Let S denote a surface and DA1, DA2, … , DAn denote the element areas of a subdivision of the surface into small area elements. Let Pi º (xi, yi, zi) denote an arbitrary point on the area element DAi. The surface integral òS gdA is defined (in the Riemann sense) as
ò
S gdA = limDA®0 S1£ i£ n g(xi, yi, zi) DAi,where DA = maxi diameter (DAi) ® 0 (the diameter of a set being the diameter of the samllest circle (in 3-D sphere) containing the set), the limit being independ of the choice of subdivision obtained by drawing a piecewise smooth mesh on S.
Let a surface be described by a two parameter vector r = r(u, v), (u, v) Î D¢, D¢ being a planar region and wite g(r) as g(u, v). The area of the approximate parallelogram points on S associated with the points (u, v), (u+Du, v) (u, v+Dv) (u+Du, v+Dv) in D¢ being r, r+ruDu, r+rvDv, r+ruDu+rvDv, is given by |ru´rv|DuDv. It follows that
òò
S gdA = òòD¢ g(u, v) |ru´rv|dudv.If the surface S is described as z = f(x,y), (x, y) Î D, i.e., r º r(x, y) = ix + jy + kf(x, y), |rx´ry| = |(i + kfx)´(j + kfy)| = |k – jfy – ifx| = Ö(1 + fx2 + fy2), so that writing g º g(x, y, f(x, y))
òò
S gdA = òòD g(x, y, f(x, y))Ö(1 + fx2 + fy2) dxdy.An oriented surface is a surface with a continuous principal normal n at each of its points. The boundary curve of such a surface is given a positive sense of traversal when it follows the fingers while the normal points in the direction of the thumb of the right hand. For an oriented surface z = f(x, y), any tangential element (idx + jdy + kdz) satisfies dz – fxdx – fydy = 0, so that the choice of an upward normal direction is given by – ifx – jfy + k, with the principal normal being n = (– ifx – jfy + k)/Ö(1 + fx2 + fy2). If v = v(x, y, z) is a vector function defined at points of S, we use the notation vn = (v)n º v×n. Hence,
òò
S (v)ndA = òòD (-v1fx –v2fy + v3)/Ö(1 + fx2 + fy2) dA = òòD (– v1fx – v2fy + v3)dxdy.The integral òòS (v)n dA is sometimes also denoted as òòS v×dA, where ‘dA’ denotes the vector area element ‘ndA’. Writing n = cos a i + cos b j + cos g k, thus cosa , cos b , cos g denoting the direction cosines of the normal to the surface at a point, thus we have: òòS (v)ndA = òòS v× ndA = òòS v×dA = òòS (v1 cos a + v2 cos b + v3 cos g ) dA = òòS (v1 dydz + v2 dzdx + v3 dxdy). Note that neglecting higher order terms "D xD y" is the projection "cos g D A" of the area element "D A" on the surface associated with the xy-plane rectangle defined by the points (x, y), (x+D x, y), (x, y+D y), (x+D x, y+D y), and similarly for "D yD z" and "D zD x".
Volume Integral
A volume integral
òòòR f dV is defined asòòò
R f dV = limDV®0 S1£ i£ n f(xi, yi, zi) DVi,in the Riemann sense, where the element volumes
DVi, 1 £ i £ n, constitute a subdivision of the volume region R into small volume elements, DV = maxi diameter (DVi), provided the limit is independent of the choice of subdivision. It is clear that the volume integral òòòR f dV is the same as the triple integral òòòR f(x, y, z)dxdydz.
The Gauss, Green and Stokes Theorems
Green’s Theorem in the plane
Let R be a closed bounded region in the xy-plane whose boundary C consists of finitely many smooth curves. Let f(x, y) and g(x, y) be functions which are continuous and have continuous partial derivatives
¶ f/¶ y and ¶ g/¶ x everywhere in some domain containing R. Then![]() .
.
Proof
: Consider R described by {a £ x £ b, p(x) £ y £ q(x)}, as well by {c £ y £ d, r(y) £ x £ s(y)}. Then,òò
R (¶f/¶y)dxdy = ò(a,b) [ò(p(x),q(x) (¶f/¶y)dy]dx = ò(a,b) [f(x, q(x)) - f(x, p(x))]dx = - òC fdx,and
òò
R (¶g/¶x)dxdy = ò(c,d) [ò(r(y),s(y) (¶g/¶x)dx]dy = ò(c,d) [g(s(y), y) - g(r(y), y)]dx = òC gdy.Combining we have òòR (¶g/¶x - ¶f/¶y)dxdy = òC (fdx+gdy). The result for a general region is proved by breaking it into a union of such regions and noting that for a common boundary of two such regions the two line integrals, being negatives of each other, cancel. #
Gauss’s Divergence Theorem
Let R be a closed bounded region in space with a piecewise smooth orientable boundary surface S. Let u(x, y, z) be a vector function which is continuous and has continuous first partial derivatives in some domain containing R. Let n denote the unit outer normal and un = u
×n the normal component of u on the boundary S of R. Then![]() .
.
Proof: Consider R described by {z1(x, y) £ z £ z2(x, y) : (x, y) Î D}, where z1, z2 describe the surfaces S1 and S2 with the upward principal normals n1 and n2. Then, writing n = cos a i + cos b j + cos g k,
òòò
R (¶u3/¶z)dV = òòD [u3(x, y, z2) - u3(x, y, z2))dxdy = òòS2 u3 cos g dA - òòS1 u3 (-cos g )dA = òòS u3 cos g dA.Adding to the above the corresponding expressions for
òòòR (¶u1/¶z)dV, and òòòR (¶u2/¶z)dV, assuming R to be described similarly with respect to x and y also, we getòòò
R Ñ×u dV = òòòR (¶u1/¶z + ¶u2/¶z + ¶u3/¶z)dV = òòS (u1 cos a + u2 cos b + u3 cos g) dA = òòS u×n dA,completing the result for the region assumed. The divergence theorem for a general region follows by breaking it into a union of such region and remembering the cancellation of the surface integrals for the common boundary surface of two regions. #
Stokes’s Theorem
Let S be a piecewise smooth oriented surface in space and let the boundary of S be piecewise smooth simple closed curve C. Let v(x, y, z) be a continuous vector function which has continuous first partial derivatives in a domain in space which contains S. Let (curl v)n = (curl v)
×n denote the normal component of curl v on the surface S, and vt = v×t the tangential component of v with respect to the boundary C of S. Then![]() .
.
Proof: By breaking the surface into a union of pieces the integrals along the common boundaries cancel and the result follows from that on the individual pieces. This enables a convenient description of each piece. Hence without loss of generality let S be such a piece and C its boundary. Let n = i cos a + j cos b + k cos g . Then
òò
S (Ñ´v)ndA = òòS [(¶v2/¶x-¶v1/¶y)cosg +(¶v3/¶y-¶v2/¶z)cosa +(¶v1/¶z-¶v3/¶x)cosb ]dA.The contribution of the terms in v1 on the right hand side equals
òòS [(-¶v1/¶y)cos g + (¶v1/¶z)cos b )] A. If S lies in a plane parallel to the yz-plane, the contributions of v1 terms are zero both in the surface and the boundary integrals. Hence without loss of generality we could describe S by z = f(x, y), (x, y) Î D (else the roles of z and y could be interchanged). Then n = (-fx i -fy j + k)/Ö(fx2 + fy2 + 1) and the surface integral evaluated as a double integral givesòò
S [(-¶v1/¶y)cos g + (¶v1/¶z)cos b )]dA = - òòD [(¶v1/¶y) + (¶v1/¶z)fy]dxdy = - òòD [¶v1(x, y, f(x, y))/¶y]dxdy=
òBd(D) v1(x, y, f(x, y))dx = = òBd(D) v1(x, y, f(x, y))(dx/ds)ds,which is the contribution of the v1 term in the boundary integral. For v2 and v3 terms the result follows by symmetry. #
Note, on the other hand, that the Green’s theorem in the plane follows from the Stokes’s theorem by considering S = R, and v = f(x, y)i + g(x,y)j.