SOME APPLICATIONS OF DIFFERENTIATION AND INTEGRATION
Area Under a Curve
The area under a curve: y = f(x)
³ 0 on [a, b], being a limit of elemental Riemann sum S f(x)D x, is given by: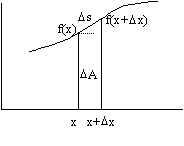
A = ò (a,b) f(x)dx.
Length of a Curve
The length of the curve y = f(x) on [a, b], being the limit of the elemental chordal sum
S
D s = S Ö [(D x)2+(f(x+D x)-f(x))2] @ S Ö [1+(f¢ (x))2)]D x, is given by:L = ò (a,b) Ö [1+(f¢ (x))2]dx.
Length of a Curve in Polar Coordinates
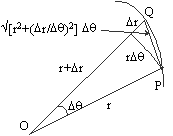
To a first order approximation the lenghth of the chord PQ,
|PQ| =
Ö [r2+(r+D r)2-2r(r+D r)cos D q ]=
Ö [(2r2+2rD r)(1-cos D q )+(D r)2)] @ Ö [r2+(D r/D q )2] D q .Hence the length of the curve from
q = a to q = b is given byL(
a , b ) = ò (a ,b ) Ö [r2+(dr/dq )2] dq .For an alternate derivation using the cartesian formula L =
ò (a,b) Ö [1+(dy/dx)2]dx, x = r cos q , y = r sin q , dy/dq = (¶ y/¶ r)(dr/dq )+¶ y/¶ q = sin q dr/dq + r cos q , dx/dq = (¶ x/¶ r)(dr/dq )+¶ x/¶ q = cos q dr/dq - r sin q and soL =
ò (a,b) Ö [(dy)2+(dx)2] = ò (a ,b ) Ö [( sin q dr/dq + r cos q )2+( cos q dr/dq - r sin q )2]dq = ò (a ,b ) Ö [r2+(dr/dq )2] dq . #Area in Polar Coordinates
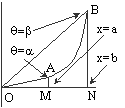
We find the area A(
a , b ) of the sector enclosed between the curve r = r(q ) and the lines q = a , and q = b . To a first order approximation the area of a sector element OPQ is ½(rD q )r = ½r2D q . Hence the required area being the limit of the Riemann sums S ½r2D q is given byA(a , b ) = ½ ò (a ,b ) r2dq .
For alternate derivation based on the cartesian formula for the area bounded by a curve y = y(x) ³ 0, x Î [a, b], and the x-axis given by
A(a, b) = ò (a,b) y(x) dx,
let q = a , b on the curve correspond to the points x = a, and x = b. Now,
area(sector OAB) = area(triangle ONB) –area(triangle OMA) - area(region MNBA)
= ½ r2(b ) sin b cos b - ½ r2(a) sin a cos a - ò (a,b) y dx
= ½r2(b ) sin b cos b - ½r2(a) sin a cos a - ò (a ,b ) (r sin q )(cos q dr/dq - r sin q ) dq
= - ò (a ,b ) sin q cos q (rdr/dq )dq + ò (a ,b ) r2 sin2 q dq + ½r2(b )sin b cos b - ½r2(a)sin a cos a
= - ½r2sin q cos q |(a ,b ) + ½ò (a ,b ) r2cos 2q dq + ò (a ,b ) r2 sin2 q dq + ½r2(b )sin b cos b -½r2(a )sin a cos a
= ½ò (a ,b ) r2 dq . #
Center of Mass
For a set of discrete masses mi placed at points (xi, yi, zi), the x, y, and z-coordinates of the center of mass are
![]() .
.
When the mass is distributed continuously along a curve, area, or volume the sums are to be replaced by appropriate integrals.
Center of Mass of a Curve
The x and the y-coordinates of the center of mass of the curve y = f(x), x
Î [a, b], (regarded as a thin wire of of length L and of uniform thickness) are given by![]() = [ò (a,b) x(ds/dx)dx]/ò (a,b) (ds/dx)dx = [ò (a,b) x Ö [1+(f¢ (x))2]dx]/L,
= [ò (a,b) x(ds/dx)dx]/ò (a,b) (ds/dx)dx = [ò (a,b) x Ö [1+(f¢ (x))2]dx]/L,
![]() = [ò (a,b) f(x)(ds/dx)dx]/ò (a,b) (ds/dx)dx = [ò (a,b) f(x) Ö [1+(f¢ (x))2]dx]/L.
= [ò (a,b) f(x)(ds/dx)dx]/ò (a,b) (ds/dx)dx = [ò (a,b) f(x) Ö [1+(f¢ (x))2]dx]/L.
Center of Mass of an Area
The x and the y-coordinates of the center of mass of the area A under the curve y = f(x)
³ 0, x Î [a, b] are![]() = [ò (a,b) xf(x)dx]/ò (a,b) f(x)dx = [ò (a,b) xf(x)dx]/A,
= [ò (a,b) xf(x)dx]/ò (a,b) f(x)dx = [ò (a,b) xf(x)dx]/A,
![]() = [ò (a,b) [f(x)/2]f(x)dx]/ò (a,b) f(x)dx = [(1/2) ò (a,b) [f(x)]2dx]/A.
= [ò (a,b) [f(x)/2]f(x)dx]/ò (a,b) f(x)dx = [(1/2) ò (a,b) [f(x)]2dx]/A.
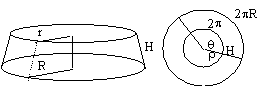
Lateral Surface Area of a Frustrum of a cone
The lateral surface area A of a frustrum of top and bottom radii r and R and slant height H is given by:
A = p (R + r) H.
To derive it, cut the surface of the frustrum along the slant height and spread in a plane to get a sector of an annulus. If
q is the angle subtended by the sector on the center and r the radius of the inner circle, r q = 2p r, (r +H)q = 2p R, so that q = 2p (R-r)/H, and hence A = (2p )-1q [p ((r +H)2-p r 2] = (1/2)q -1Hq (2r +H) q = (1/2)(H/[2p (R-r)]) 2p (R-r)2p (R+r) = p H(R+r). #Surface of Revolution
A line element of length
D s with end points distant f(x) and f(x+D x) rotated about the x-axis generates the lateral surface of a frustrum of area p (f(x)+f(x+D x))D s @ 2p f(x)D s. Hence if a rectifiable curve y = f(x) ³ 0, x Î [a, b] is rotated about x-axis, the surface area generated, being the limit of the elemental sum S 2p f(x)D x, is given bySrev = ò (a,b) 2p f(x)(ds/dx)dx = 2p ò (a,b) f(x)Ö [1+(f¢ (x))2]dx.
Srev = 2p ![]() ´ L (Pappus theorem),
´ L (Pappus theorem),
i.e., the surface of revolution equals the distance travelled by the center of mass of the curve multiplied by the length of the curve.
Example. The surface of revolution of a circle of radius R whose center is at a distance H > R from the x-axis is given by S = 2
p H´ 2p R.Example. The center of mass of a semi-circular arc of radius R is distant 4
p R2/(2p ´ p R) = (2/p )R from the center.Volume of Revolution
Let the continuous curve y = f(x)
³ 0 on [a, b] be rotated about the x-axis. The volume of the solid generated under the curve is given by: Vrev = p ò (a,b) [f(x)]2 dx, which is obtained as the limit of the sum of volumes of the disks S i p [f(xi)]2(xi+1 – xi), where xi’s constitute a subdivision of the interval [a, b]. ClearlyVrev = 2p ![]() ´ A (Pappus theorem),
´ A (Pappus theorem),
i.e., the volume of revolution equals the distance travelled by the center of mass of area multiplied by the area.
Example. The volume of revolution of a circle of radius R whose center is at a distance H > R from the x-axis is given by S = 2
p H´ p R2.Example. The center of mass of a semi-circular disc of radius R is distant (4/3)
p R3/(2p ´ p R2/2) = [4/(3p )]R from the center.Volume by Slicing
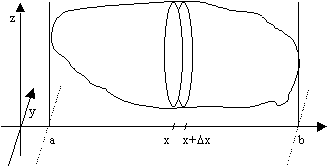
Suppose a solid object has boundaries extending from x = a, to x = b, and that its cross-section in a plane passing through (x, 0, 0) and parallel to the yz-plane has area A(x). To a first order approximation, the volume of the slice of the object on the right to the plane of thickness
D x is then A(x)D x so that the volume of the solid is the limit of the elemental sum S A(x)D x. This being a Riemann sum, the volume is given by the formulaV = ò (a,b) A(x) dx.
The Stirling’s Formula for the Factorial and the Gamma Function
The Gamma function
G (a), (a > 0) is defined byG
(a) = ò (0,¥ ) e-tta-1dt.The improper integral is convergent for all complex a with Rl a > 0. The Gamma function satisfies an important recurrence relation
G
(a+1) = aG (a).Proof
: Integrating by parts, G (a+1) = ò (0,¥ ) e-ttadt = [tae-t](0,¥ ) + aò (0,¥ ) e-tta-1dt = G (a). #Noting that
G (1) = ò (0,¥ ) e-tdt = 1, it follows that G (2) = 1, G (3) = 2G (2) = 2!, G (4) = 3G (3) = 3!, … , so that in generalG
(n+1) = n!, n = 0, 1, 2, 3, … .Another useful constant is
G
(1/2) = Ö p .Proof
: Putting t = s2, s = t1/2, so that ds = ½t-1/2dt, and, G (1/2) = ò (0,¥ ) e-tt-1/2dt = 2ò (0,¥ ) exp[-s2] ds, i.e.,G
(1/2) = ò (-¥ ,¥ ) exp[-x2]dx.To evaluate the integral, let I =
ò (-¥ ,¥ ) exp[-x2]dx. ThenI2 =
ò (-¥ ,¥ ) exp[-x2]dx ò (-¥ ,¥ ) exp[-y2]dy = ò (-¥ ,¥ ) ò (-¥ ,¥ ) exp[-(x2+y2)]dxdy.Using the polar coordinates
I2 =
ò (0,2p ) ò (0,¥ ) exp[-r2]rdrdq = p ò (0,¥ ) exp[-t]dt = p ,so that I =
Ö p . #Next we derive the Stirling’s formula for the Gamma function:
G
(a) @ (2p )½e-aaa-½, a ® ¥ .Proof
: Putting t = ax, G (a) = aa ò (0,¥ ) e-axxa-1dx. For the function f(x) = e-xx, f¢ (x) = e-x(1-x). Hence f(x) increases on [0, 1] and decreases on [1, ¥ ), and therefore on the interval [0, ¥ ), the function e-xx has maxima at x = 1. Hence,(e-aaa-½)-1aa
ò |x-1|³ d e-axxa-1dx £ a½ ò |x-1|³ d (e-xx/e-1)a-1e-xdx = a ½(e-(1+d )(1+d ))a-1 ® 0, a ® ¥ ,where we have used:
[e-(1+
d )(1+d )]/[e-(1-d )(1-d )] = [e-2d (1+d )/(1-d )] = [1+2(d +d 2+d 3+…)]/[1+2d +(2d )2/2!+ (2d )3/3!+…] > 1.Expanding the function ln x about the point x = 1, by the mean value theorem
ln x = (x-1) -[(x-1)2/2!](1/
x 2),for some
x lying between 1 and x. Hence, with x = x x Î (1-d , 1+d ),(e-aaa-½)-1aa
ò |x-1|<d e-axxa-1dx = a ½ ò |x-1|<d (e-(x-1)x)ax-1dx = a ½ ò |x-1|<d (e-(x-1)+lnx)ax-1dx= a ½ ò |x-1|<d exp[a{-(x-1)+(x-1)-((x-1)2/2!)x -2}]x-1dx
= a ½ ò |x-1|<d exp[-a((x-1)2/2!)x -2] x-1dx.
Now,
a½ ò |x-1|<d exp[-a((x-1)2/2)(1-d )-2](1+d )-1dx
£
a½ ò |x-1|<d exp[-a((x-1)2/2!)x -2]x-1dx£
a½ ò |x-1|<d exp[-a((x-1)2/2)(1+d )-2](1-d )-1dxPutting x = 1 + (2/a)½t(1+
d ),a½
ò |x-1|<d exp[-a((x-1)2/2)(1+d )-2](1-d )-1dx = a½ ò |t|<d Ö (a/2)/(1+d ) exp[-t2](1-d )-1(2/a)½(1+d )dt@
[(1+d )/(1-d )]2½ ò (¥ ,¥ ) exp[-t2]dt= [(1+
d )/(1-d )]Ö (2p ).Similarly,
a½
ò |x-1|<d exp[-a((x-1)2/2)(1-d )-2](1+d )-1dx @ [(1-d )/(1+d )]Ö (2p ).Hence,
[(1-
d )/(1+d )]Ö (2p ) £ lima® ¥ (e-aaa-½)-1G (a) £ [(1+d )/(1-d )]Ö (2p ),and letting
d ® 0, we get lima® ¥ (e-aaa-½)-1G (a) = Ö (2p ), i.e., G (a) @ Ö (2p ) e-aaa-½, a ® ¥ , completing the proof of the Stirling’s formula. #Clearly, the Stirling’s formula for the asymptotic evaluation of n! can be derived from the Stirling’s formula for the Gamma function. thus n! =
G (n+1) = nG (n) @ n(2p )½e-nnn-½, n ® ¥ , so thatn! @ (2p )½e-nnn+½, n ® ¥ . (Stirling’s formula for n!)
An asymptotic evaluation of the semi-factorials m!! could be done by using:
2n!!
º 2× 4× 6…(2n-2)× 2n = 2nn! @ (2p )1/2e-nnn+1/22n; (2n+1)!! º 1× 3× 5…(2n-1)× (2n+1) = (2n+1)!/(2n)!!.
Convergence of the Binomial Expansion on [-1, 1]
Theorem. For a > 0, the binomial expansion
(1+x)a = 1+S n³ 1 [a(a-1)(a-2)…(a-n+1)/n!]xn,
is valid for x Î [-1, 1], and, the convergence of the binomial series is uniform on [-1, 1].
We shall prove this result in due course of time. However, note that for the binomial series the limit ratio
limn
® ¥ |an+1/an| = limn® ¥ |(a-n)/(a-n+1)x| = |x|,so that the series converges for |x| < 1, and diverges for |x| > 1.
Note that the convergence of a Taylor’s series does not automatically imply that its sum equals the function value – for example, for the function f(x) defined by
![]()
for x
¹ 0, f¢ (x) = (2/x3)f(x) is a polynomial in 1/x multiplying exp{-1/x2}. Differentiating this relation it follows that for all n ³ 1, f(n)(x) is a polynomial in 1/x multiplying exp{-1/x2}. Since for n ³ 0, x-nexp{-1/x2} = [xnexp 1/x2]-1 ® 0, x ® 0, it follows that f(n)(0) = 0, n ³ 1. Hence each term in the Taylor’s expansion S n³ 0 xnf(n)(0)/n! of f(x) about x = 0 is zero. Since the function is positive for each x ¹ 0, the Taylor’s expansion does not represent the value of the function.Hence to prove that the Taylor’s expansion represents the function, it is necessary to show that the remainder Rn(x) tends to zero as n
® ¥ , wheref(x) = S 0£ n£ m (x-a)nf(n)(a)/n! + Rm+1(x).
Note that in a Taylor’s expansion about x = 0, the Cauchy’s form of remainder after n-terms is
Rn(x) = [f(n)(
x )/n!]xn,where
x = q x, with 0 < q < 1. Note that x = x (x, n), and, q = q (x, n). To analyze the binomial expansion for f(x) = (1+x)a, let 0 £ m-1 < a < m, m ³ 1. As, f(n)(x ) = [a(a-1)(a-2)…(a-n+1)](1+x )a-n,|Rn(x)| = [a(a-1)(a-2)…(a-m+1)(-1)n-m(m-a)… (n-a-2)(n-a-1)/n!] (1+
x )a-n xn= [a(a-1)(a-2)…(a-m+1)(-1)n-m{
G (n-a)/G (m-a)}/n!] (1+x )a-n xn@
[a(a-1)(a-2)…(a-m+1)(-1)n-m/G (m-a)]exp{a}(n-a)n-a-1/2/(nn+1/2] (1+x )a-n xn= [a(a-1)(a-2)…(a-m+1)(-1)n-m/
G (m-a)]exp{a}(1-a/n)n-a-1/2na-2] (1+x )a-n xn@
[a(a-1)(a-2)…(a-m+1)(-1)n-m/G (m-a)]na-2 (1+x )a-n xn.For whatever
q Î (0, 1), and ½ > d > 0, |x/(1+q x)| < 1-d for x in [0, 1-d ], and for x in [-1/2 + d , 0], |x/(1+q x)| < (½ - d )/(1/2 + d ) , i.e., |x|/|1+q x| < max {1-d , (½ - d )/(1/2 + d )} provided x Î [-1/2+d , 1-d ]. Hence, this asymptotic estimate shows that Rn(x) ® 0, as n ® ¥ , if (i) –1/2 < x < 1, and (ii) if a < 2 and x = ½, 1. Moreover, the convergence is uniform for x Î [-1/2+d , 1-d ]. In the remaining cases because of unknown nature of x the estimate doesn’t say much. Hence there is a need for a better form of remainder in the Taylor’s expansion.Taylor’s Expansion with an Integral form of Remainder. Let f(x) be n+1 times continuously differentiable in the interior of an interval containing a and x and be continuous on the interval. Then,
f(x) = S 0£ k£ n f(k)(a)(x-a)n/n! + (n!)-1 ò (a,x) f(n+1)(t)(x-t)ndt.
Proof
: For n = 0, the formula reads f(x) = f(a) + ò (a,x) f¢ (t)dt, which is true by the fundamental theorem of integral calculus. Hence assuming the formula for ‘n’ and the hypothesis for ‘n+1’ an integration by parts givesf(x) =
S 0£ k£ n f(k)(a)(x-a)n/n! + f(n+1)(a)(x-a)n+1/(n+1)! + (1/(n+1)!) ò (a,x) f(n+2)(t)(x-t)n+1dt,which is the formula for the case ‘n+1’, completing the proof. #
Proof of the Convergence of the Binomial Expansion: By the integral form of remainder in the binomial series
Rn(x) = [(n-1)!]-1
ò (0,x) a(a-1)…(a-n+1)(1+t)a-n(x-t)ndt= xn+1[(n-1)!]-1
ò (0,1) a(a-1)…(a-n+1)(1+xs)a[(1-s)/(1+xs)]nds,putting t = xs. For n > a, the magnitude of Rn(x) over the interval [-1, 1] is maximum when x = -1. This is because the factors |x|n+1 and (1+xs)a-n, s
Î (0, 1) both are maximum at x = -1 in the interval [-1, 1]. Hencemaxx
Î [-1,1] |Rn(x)| = [(n-1)!]-1 ò (0,1) |a(a-1)…(a-n+1)|(1-s)ads= [a(a-1)…(a-m+1){
G (n-a)/G (m-a)}/(n-1)!] ò (0,1) (1-s)ads@
[a(a-1)…(a-m+1)/G (m-a)]exp{a}(n-a)n-a-½ n-n+½ ò (0,1) [-(1-s)a+1/(a+1)](0,1)@
[a(a-1)…(a-m+1)/G (m-a)]n-a(a+1)-1 ® 0, n ® ¥ . #Note that the order of the rate of convergence of maxx
Î [-1,1] |Rn(x)| is O(n-a). Thus, we have proved that the binomial series expansion S n³ 0 [a(a-1)(a-2)…(a-n+1)/n!]xn of (1+x)a, a > 0, converges uniformly to the function (1+x)a on the interval [-1, 1]. Hence the applicability of the integral form of the remainder!Corollary. The function |x| can be uniformly approximated on [-1, 1] by a sequence of algebraic polynomials.
Proof
: In the binomial expansion |x| = Ö (x2) = Ö (1-[1-x2]) = 1-(1/2)[1-x2] -S n³ 2 2-n[1× 3× 5× …× (2n-3)!!/n!](1-x2)n, since 1-x2 Î [-1, 1] the uniform convergence of the series implies that the truncated sums which are algebraic polynomials in x converge to |x| uniformly on [-1, 1]. #Uniform Approximation of Functions in C[0, 1]
Theorem (Polygonal Approximation). If f(x) Î C[0, 1], given any e > 0 there exists a polygon W (x) such that |f(x) - W (x)| < e , for all x Î [0, 1].
Proof
: Since a continuous function on a closed interval is uniformly continuous, given an arbitrary e > 0, there exists a d > 0, such that |f(x)-f(y)| < e , whenever |x-y| < d . Take n > 1/d , define xk = k/n, 0 £ k £ 1, and consider the polygon W n(x), x Î [0, 1], obtained by joining the points (xk, f(xk)) and (xk+1, f(xk+1)), 0 £ k < n, by straight line segments. Note thatW
n(x) = [(xk+1-x)/(xk+1-x)]f(xk) + [(x-xk)/(xk+1-x)]f(xk+1), xk £ x £ xk+1, 0 £ k < n..Let x
Î [0, 1]. We have a 0 £ k < n such that xk £ x £ xk+1. Then, clearly,|f(x)-
W n(x)| £ (xk+1-x)/ (xk+1-xk)|f(xk)-f(x)| + (x-xk)/(xk+1-xk)|f(xk+1)-f(x)| < e ,i.e., |f(x)-
W n(x)| < e , x Î [0, 1], saying that f(x) is uniforly approximated by the polygons W n(x). #Theorem (Representation of Polygons). If W n(x) is a polygon on [0, 1] with the n-distinct break points xk Î (0, 1), 1 £ k £ n, n ³ 0, there exist constants ak, 0 £ k £ n+1, such that:
W
n(x) = a0 + S1£ k£ n ak|x-xk| + an+1x, x Î [0, 1].Proof
: Without loss of generality we could assume that 0 = x0 < x1 < x2 < … < xn < xn+1 = 1. The case without break points, i.e., n = 0 corresponds to a linear function and and is true. For n = 1 we have to show that the following system of linear equations is solvable:a0 + (x1-x0)× a1 + 0× a2 = W 1(0)
a0 + 0× a1 + x1× a2 = W 1(x1)
a0 + (1-x1)× a1 + 1× a2 = W 1(1),
which is true as the matrix of the system is
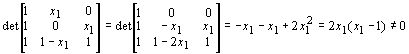 .
.
Now, the graph of W n(x) on the interval [xn-1, xn+1] is a polygon with one break point. Let W 1(x) denote the polygon on [0, 1] obtained by extending this part on [0, 1] so that on [x0, xn] the graph is linear. Since W 1(x) has one break point on (0, 1), W 1(x) = a + bx + c|x-xn|. Then the function W n-1(x) = W n(x)- W 1(x) is a polygon with break points x1, x2, … , xn-1 only. Accordingly, assuming the result for (n-1)-break points, it has the form W n(x) - W 1(x) = W n-1(x) = b0 + S 1£ k£ n-1 bk|x-xk| + bnx, for some constants bk’s. From this it follows that W n(x) = W 1(x) + W n-1(x) = a + bx + c|x-xn| + b0 + S 1£ k£ n-1 bk|x-xk| + bnx = a0 + S 1£ k£ n ak|x-xk| + an+1x, where a0 = a + b0, an+1 = b + bn, an = c, and ak = bk, 1 £ k £ n-1, proving the result for n-break points. The theorem follows. #
Weierstrass’ Approximation Theorem. If f(x) Î C[0, 1], given any e > 0 there exists an algebraic polynomial P(x) such that |f(x) - P(x)| < e , for all x Î [0, 1].
Proof
: Using the polygonal approximation theorem, f(x) can be uniformly approximated to within e /2 by a polygon W n(x) = a0 + S 1£ k£ n ak|x-xk| + an+1x, say. Since for x Î [0, 1], |x-xk| < 1, x-xk Î [-1, 1]. Hence each |x-xk|, 1 £ k £ n, can be approximated to within (e /2)/S 1£ j£ n |aj| on [0, 1] by a polynomial in (x-xk) and therefore in x. Calling this polynomial Pk(x) and putting P(x) = a0 + S 1£ k£ n akPk(x) + an+1x, we have |f(x) - P(x)| £ |f(x) - W n(x)| + |W n(x) - P(x)| < e /2 + |S 1£ k£ n ak [|x-xk| - Pk(x)]| £ < e /2 + |S 1£ k£ n |ak| (e /2)/S 1£ j£ n |aj| = e , completing the proof. #Quadratic Surfaces
A general quadratic equation in the three space variables X, Y, Z is: AX2+BY2+CZ2 + 2HXY+2GXZ+2FYZ + LX+MY+NZ + C = 0. If A, B, C, H, G, F are all zero it reduces to a linear equation LX + MY + NZ + C = 0, which, if at least one of L, M, N is non-zero, represents a plane with the direction ratios of the normal to the pla being L, M, N. If also L, M, N are all zeros the equation represents nothing.
In the proper quadratic case when at least one of A, B, C, H, G, F is non-zero, the homogeneous second degree terms constitute a non-zero real quadratic form Q(X, Y, Z) = AX2+BY2+CZ2+2HXY+2FYZ+2GXZ. The matrix
H = ![]()
of the quadratic form Q, being real symmetric, has real eign-values
l , m , n and the associated orthonormal eigen-vectors u, v, w Î R 3, so that [u | v | w]¢ H[u | v | w] = diag (l , m , n ), and with U = [u | v | w], Q(X, Y, Z) = [X Y Z]H[X Y Z]¢ = [X Y Z]U(U¢ HU)U¢ [X Y Z]¢ = l x2 + m y2 + n z2, where (x, y, z) = (X Y Z)U are the coordinates of the point P = (X, Y, Z) with respect to the new orthogonal coordinate system with the axes in the direction of the unit vectors u, v, w. So in the new co-ordinate system the quadratic equation becomesl
x2 + m y2 + n z2 + lx + my + nz + c = 0.For the coefficients of
l , m , n there arise the follwing cases:(I) Only one of
l , m , n is non-zero, in which, without loss of generality, we can consider the case l , m = 0, n > 0. The equation then is: n z2 + lx + my + nz + c = 0. The term in z could be eliminated by a change of coordinate system: z ® z – ½n/n of taking the origin (0, 0, ½n/n ). Division by n leads to the equation z2 + l1x + m1y + c1 = 0.(A) If l1, m1 = 0, we get: nothing, if c1 > 0, a single plane, z = 0, if c1 = 0, and a pair of parallel planes, z =
± Ö (-c1), if c1 < 0.(B) If at least one of l1, m1 is non-zero we change the coordinate system by shifting the origin to a point on the line l1x + m1y + c1 = 0 in the xy-plane through: x
® x+h, y ® y+k, where h and k are arbitrarily chosen so that l1h + m1y + c1 = 0. The equation now becomes z2 + l1x + m1y = 0. Next we rotate the xy-coordinate axes by an angle q so that the new x-axis lies in a dirction along the line l1x + m1y = 0 in the xy-plane through![]() ,
,
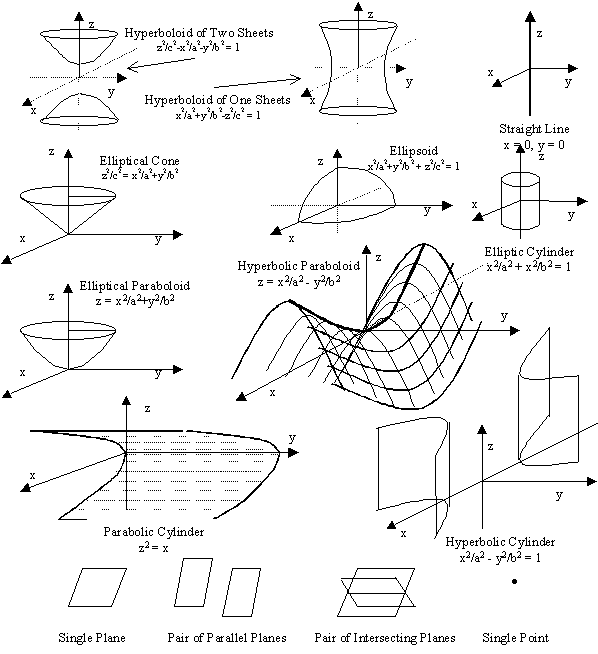
i.e., x ® x cos q -y sin q , y ® x sin q + y cos q , so that l1x + m1y ® l1 (x cos q -y sin q ) + m1 (x sin q + y cos q ) = (l1 cos q + m1 sin q ) x + (-l1 sin q + m1 cos q ) y. Choosing: sin q = l1/Ö (l12+m12), cos q = -m1/Ö (l12+m12), the equation becomes 0 = z2 + l1 [x(-m1/Ö (l12+m12)–y(l1/Ö (l12+m12))] + m1 [x(l1/Ö (l12+m12)+ y(-m1/Ö (l12+m12))] = z2 - yÖ (l12+m12), which on putting c2 = Ö (l12+m12), gives: z2/c2 = y, a parabolic cylinder with axis along the x-axis.
(II) Two of l , m , n non-zero and one zero, when without loss of generality, we take n = 0. Two cases arize:
(A) l , m of the same sign, when without loss of generality we can assume that l , m > 0. The equation is now l x2 + m y2 + lx + my + nz + c = 0. By a change of origin the term lx + my can be removed and we get the equation as: l x2 + m y2 + nz + c1 = 0.
If n = 0, and c1 > 0 we get nothing from l x2 + m y2 + c1 = 0.
If n = 0, and c1 = 0 we get l x2 + m y2 = 0, which gives a straight line: x = 0, y = 0, viz., the z-axis.
If n = 0 and c1 < 0, l x2+m y2 = -c1, which by putting -c1/l = a2, -c1/m = b2 gives: x2/a2 + y2/b2 = 1, an elliptic cylinder with axis along the z-axis.
If n ¹ 0, changing the origin at (0, 0, c/n) i.e., by z ® z-c/n, the equation becomes l x2 + m y2 + nz = 0, which is of one of the types: x2/a2 + y2/b2 = z, an elliptical paraboloid (upward), x2/a2 + y2/b2 = -z, another elliptical paraboloid (downward).
(B) l , m of the opposite signs, when without loss of generality we let l > 0, m < 0. From the equation l x2 + m y2 + lx + my + nz + c = 0, again, by a change of origin we remove the term lx + my to get: l x2 + m y2 + nz + c1 = 0.
If n = 0, the equation becomes l x2 + m y2 + c1 = 0. Then, if c1 = 0, the equation reduces to (y-mx)(y+mx) = 0, m = Ö (-l /m ) ¹ 0, representing a pair of intersecting planes y = ± mx and, y = -mx; and if c1 ¹ 0, the equation simplifies to x2/a2 - y2/b2 = 1, or to y2/b2 - x2/a2 = 1, each of which represents a hyperbolic cylinder.
If n ¹ 0, the equation is: l x2 + m y2 + n(z + c1/n) = 0, which by a change of origin to (0, 0, c1/n) becomes l x2 + m y2 + nz = 0, which depending on the sign of n is of one of the types: x2/a2 - y2/b2 = z, a hyperbolic paraboloid, or, y2/a2 - x2/b2 = z, which is also a hyperbolic paraboloid.
(III) All three of l , m , n non-zero, in which case there arise two situations:
(A) All of l , m , n have the same sign, in which case, without loss of generality we can assume l , m , n > 0. Then, from the equation l x2 + m y2 + n z2 + lx + my + nz + c = 0 by a change of origin to (½l/l , ½m/m , ½n/n ), i.e., by the transformations: x ® x – ½l/l , y ® y – ½m/m , z ® z – ½n/n , the term lx + my + nz could be removed so that the equation becomes l x2 + m y2 + n z2 + c1 = 0. If c1 > 0, nothing is represented by the equation. If c1 = 0, it represents a singleton point (0, 0, 0). If c1 < 0, the equation can be re-written in the standard form: x2/a2 + y2/b2 + z2/c2 = 1, representing an ellipsoid.
(B) Two of l , m , n have the same sign and one an opposite sign, when without loss of generality we can assume l , m > 0, n < 0. Then, as before, by the change of origin to (½l/l , ½m/m , ½n/n ), the term lx + my + nz could be removed and the equation becomes l x2 + m y2 + n z2 + c1 = 0.
If c1 = 0, the equation can be put in the standard form: x2/a2 + y2/b2 = z2/c2, an elliptical cone.
If c1 > 0, the equation can be put in the form: x2/a2 + y2/b2 - z2/c2 = 1, a hyperboloid of one sheet.
If c1 < 0, the equation can be put in the form: z2/c2 - x2/a2 - y2/b2 = 1, a hyperboloid of two sheets.
Hence we have proved that a quadratic equation in x, y, z could represent one of the following:
(1) nothing, (2) a single point, (3) a straight line, (4) a single plane, (5) a pair of parallel planes, (6) a pair of intersecting planes, (7) a parabolic cylinder, (8) an elliptic cylinder, (9) a hyperbolic cylinder, (10) an elliptical cone, (11) an elliptical paraboloid, (12) a hyperbolic paraboloid, (13) an ellipsoid, (14) a hyperboloid of one sheet, and (15) a hyperboloid of two sheets.
Serret-Frenet Formulae
Space Curves
Let r(t) = (x(t), y(t), z(t))
¢ , a £ t £ b, denote a space curve. Consider two points P and Q on the curve associated with the values t and t+D t. The vector obtained by joining the point P to the point Q is by D r = r(t+D t)-r(t). The arc-length s(t) is the length of the curve between the points r(a) and r(t) and is given bys(t) = ò (a,t) |dr(t)/dt|dt,
and the rate of change of arc-length with respect to the parameter t is
ds/dt = |dr(t)/dt|. The rate of change of the position vector r(t) of the point P on the curve with respect to t is the vector dr(t)/dt = limD t® 0 D r/D t, which gives the direction of the tangent to the curve at P.The Unit Tangent and the Principal Normal
The rate of change of r(t) with respect to the arc-length parameter is:
r¢ = dr/ds = (dr/dt)/(ds/dt) = (dr(t)/dt)/|dr(t)/dt| = u. Here, we follow the convention of using the prime to denote the derivatives with respect to the arc-length parameter. Since it is of unit magnitude, it is called the unit tangent vector on the curve at P. The plane in which the tangent locally moves is the plane containing the unit tangent u and its rate of change du/dt.Differentiating the relation
u2 º |u|2 = u× u = 1, we find u× u¢ = 0, i.e., the rate of change of the unit tangent is in a direction orthogonal to that of the unit tangent (as is the case with all unit vectors). This gives the direction of the principal normal to the curve at P with the unit principal normal p given byp = u¢ /|u¢ | = (du/dt)/|du/dt|.
The quantity |u
¢ | is called the curvature of the curve at P and is denoted by the Greek letter kappa k , so thatu¢ = k p,
so that the unit tangent changes in the direction of the principal normal with the curvature as the proportionality constant. Note that for a linear curve the curvature
k equals zero and the direction of the principal normal p remains undefined.The Osculating, Normal and Rectifying Planes and the Unit Binormal
The plane containing the unit tangent u and and the principal normal p is called the osculating plane and the unit vector u
´ p the unit binormal b so that: b = u´ p. The plane containing principal normal p and the binormal b is called the normal plane, and the one containing the unit tangent u and the binormal b is the rectifying plane.The rate of change of the principal normal lies in the plane of u and b, so that p
¢ = t b – ku, for some constants t and k. Using p = b´ u, p¢ = b¢ ´ u + b´ u¢ = (u´ p)¢ ´ u + b´ k p = [(u¢ ´ p)´ u + (u´ p¢ )´ u] - k u =(u´ p¢ )´ u - k u = (u´ [t b-ku])´ u - k u = t (-p)´ u - k u = t b - k u, so that k = k and we havep¢ = t b – k u.
As, b
¢ = u¢ ´ p + u´ p¢ = u´ p¢ = u´ (t b – k u), we haveb¢ = -t p.
The quantity
t is called the torsion of the curve at P and it follows that the binormal changes in the direction of the normal with the proportionality constant -t . Note that for a planar curve the torsion t equals zero.The relations:
u¢ = k p, p¢ = t b – k u, b¢ = -t p, are known as the Serret-Frenet formulae.Note that by definition
k ³ 0, and, |r² | = k . As, r¢ = u, r² = k p, r¢ ¢ ¢ = k ¢ p + k [t b - k u], [r¢ r² r¢ ¢ ¢ ] = u× (k p´ [k ¢ p + k (t b-k u)]) = u× [k 2(t u + k b)] = k 2t , So that we have the formula: t = [r¢ r² r¢ ¢ ¢ ]/k 2.Also, for differentiation with respect to the parameter t, dr/dt = r
¢ (ds/dt) = u(ds/dt), d2r/dt2 = r² (ds/dt)2 + r¢ (d2s/dt2) = k p(ds/dt)2 + u(d2s/dt2), d3r/dt3 = r¢ ¢ ¢ (ds/dt)3 + 3r¢ ¢ (ds/dt)(d2s/dt2) + r¢ d3s/dt3 = (k ¢ p+k [t b - k u]) (ds/dt)3 + 3k p(ds/dt)(d2s/dt2) + u(d3s/dt3), i.e., d3r/dt3 = [-k 2(ds/dt)3+(d3s/dt3)]u + [k ¢ +(ds/dt)3+3k (ds/dt) (d2s/dt2)]p + k t b.Some inner products and a scalar triple product involving derivatives with respect to the parameter t are:
(dr/dt)2 = (ds/dt)2, (dr/dt)
× (d2r/dt2) = (ds/dt)× (d2s/dt2), (d2r/dt2)2 = k 2((ds/dt)4 + (d2s/dt2)2.[dr/dt d2r/dt2 d3r/dt3] = (uds/dt
´ [k p(ds/dt)2 + u(d2s/dt2)])× d3r/dt3 = k (ds/dt)3b× (k t b) = k 2t (ds/dt)3.As, [(dr/dt)2][(d2r/dt2)2]–[(dr/dt)
× (d2r/dt2)]2 = (ds/dt)2[k 2((ds/dt)4+(d2s/dt2)2]–[(ds/dt)× (d2s/dt2)]2 = k 2((ds/dt)6,![]() ,
, ![]() .
.
Velocity and Acceleration
If r(t) denotes the position vector of a moving point in the space at time t, and v(t), a(t) its velocity, and acceleration vectors, respectively, we have
v(t) = dr/dt = (ds/dt)u,
a(t) = dv/dt = d2r/dt2 = (d2s/dt2)u + k (ds/dt)2p,
from which we observe that the direction of the velocity of the particle is along the tangent of its trajectory, but that its acceleration has two components (i) the tangential accelearation (d2s/dt2)u, along the direction of the tangent, and, (ii) the normal accelearation
k (ds/dt)2p, along the direction of the principal normal. This second term is due to the curvature k of the trajectory. This normal acceleration is related with the terms known as centripetal and Coriolis accelerations, respectively, in a circular motion with a constant angular velocity, and, in a motion with constant speed along a radial line on a rotating disk, or along a meridian on a rotating sphere..