A group consists of a non-empty set G along with a binary operation "* " ( * : G´ G ® G), satisfying the following group axioms:

(1) If a, b, c Î G, then a* (b* c) = (a* b)* c; i.e., * is associative.(2) There exists an element e Î G such that for any a Î G, a* e = e* a = a.(3) For any a Î G, there exists an element a Î G such that a* a = a * a = e.

It is easy to verify that e, called the identity element of the group G, is unique. For any a Î G, the element a as in (3), called an inverse of a, is also unique.

A group is called finite if it has only a finite number of elements in it. Otherwise, we say that the group is infinite. The number of elements in a group, or its cardinality, is called the order of the group.

The sets of complex numbers C, real numbers R, rational numbers Q and integers Z are groups under the binary operation "+", the ordinary addition of real numbers. In this case e = 0 and a = -a. The sets of non-zero real numbers, non-zero rational numbers, positive real numbers, positive rational numbers etc. are groups under the binary operation "´ ", the ordinary multiplication of real numbers. In this case e = 1 and a = a^-1 = 1/a. These two examples, utilizing the ordinary addition and multiplication, have motivated the phrases: additive group (the binary operation "* " is written as "+", e is called the zero or the additive identity and is written as 0, a is called the negative or the additive inverse of a and is written as -a) and multiplicative group (in which case, the binary operation * is usually written as ". " or is omitted altogether (i.e., a.b or ab represent a* b), e is called the unity or the multiplicative identity and is written as 1; a is called the multiplicative inverse of a and is written as a^-1). In a multiplicative group a^m means a* a* ... * a (m-times). Thus a³ = a* a* a. In an additive group, similarly, ma denotes the addition or sum of m number of a's.

A group G is called commutative if for all a, b Î G there holds a* b = b* a, i.e., a and b commute.

A subgroup H of a group G is a subset which under the same binary operation is itself a group. Two groups G and G' are said to be isomorphic if there exists a 1-1 onto map h : G ® G' such that h (ab) = h (a)h (b) for all a, bÎ G. We say that h is an isomorphism from G to G', while it follows that h ^-1 is an isomorphism from G' to G.

1. Show that the following sets, with the ordinary addition as the binary operation, constitute groups : (i) the set Z of integers; (ii) the set Q of rational numbers; (iii) the set R of real numbers; (iv) m + Ö 2n : m, n Î Z}; (v) the set C of complex numbers.

2. Show that the following sets, with the ordinary multiplication as the binary operation, constitute groups: (i) the set R\{0} of non-zero reals; (ii) the set Q\{0} of non-zero rational numbers; (iii) the set C\{0} of non-zero complex numbers; (iv) {1, -1}; {p + qÖ 2 : p, q Î Q}; (v) the set {1, w , w ²} of cube roots of 1; (vii) {1, i , -i , -1}; (vi) {exp (i 2p j/n) : 0 < j < n}.

3. Show that the set of planar vectors u = x i + y j is a subgroup of the group of spacial (3-d) vectors v = x i + y j + z k, with the ordinary vector addition as the binary operation. Here i, j, k are the standard unit vectors in the x, y and z directions.

4. Show that a subset H of a Group G is a subgroup of G if a^-1b Î H whenever a, b Î H. What happens if "a^-1b" in the previous statement is replaced by "ab "?

Let S be an ordered set. A 1-1 onto map s : S ® S is called a permutation on S. Defining the product s s ' of two permutations s and s ' to be the ordinary composition of them regarded as maps, i.e., s s '(s) = s (s '(s)), s Î S, it is easily verified that the set P _S of all permutations on S is a group. P _S is called a group of permutaitons. A permutation s is often identified with the new ordering "<<" (s << s' if s ^-1(s) < s ^-1(s'), where "<" is the original ordering in S) that it induces on S.

Theorem (Cayley). Any group G is isomorphic to a subgroup of a group of permutaitons.

Proof: Consider the permutation group P _G. For a Î G define the permutation s by s _a(g) = ag. The set G' = {s _a : a Î G} is easily verified to be a subgroup of P _G. Noting that s _a s _b (g) = a(bg) = (ab)g = s _ab , and defining h : G ® G' by h (a) = s _a, it follows that h is an isomorphism from G to G'. #

1. S_n, the permutation group corresponding to the ordered set {1,2, ... ,n} of the first n positive integers, has n! elements in it. It is isomorphic to the group of permutations on any ordered set of n elements.

2. Let s Î S_n. Identifying s with the ordered sequence (s (1), s (2), ... , s (n)) for each k = 1, 2, ... , let n _k denote the number of s (j)'s which occur on the right of s (k) and are smaller than s (k). Thus n _k is the number of negative entries in the sequence s (k+1)- s (k), s (k+2)- s (k), s (k+3)- s (k), ... , and is termed the number of inversions in s relative to its k-th entry. Let n (s ) denote the total number of inversions in the permutaiton s , i.e., n (s ) = n ₁ + n ₂ + n ₃ + ... + n _n (actually n _n = "0"!). The sign of a permutation s is defined as sgn s = (-1)n ^{(s )} , and it is +1, if n (s ) is even and -1, if n (s ) is odd. Accordingly, we talk about s being an even permutation or an odd permutation, respectively. For n > 2, show that there exist exactly n!/2 odd permutaitons.

3. The set of even permutations in S_n, denoted by A_n, is called an alternating group. Show that A_n is a subgroup of S_n.

4. Prove that sgn (s _{1s 2}) = (sgn s ₁)(sgn s ₂), s ₁, s _{2 Î} S_n. Deduce that sgn s ^-1 = sgn s .

5. Let s , s ' be two permutations in S_n such that s (i) = s '(i), i ¹ k, k+1 for some k, while s (k) = s '(k+1). show that s (k+1) = s '(k) and that sgn s = - sgn s '.

6. If s Î S_n is such that s (k) = k, k ¹ i, j, while s(i) = j (Þ s(j) = i), s is called a transposition and is denoted by (i,j). Show that any permutation can be written as a product of an odd or even number of transpositions according as the permutation is odd or even.

7. More generally, s Î S_n is called a cyclic permutation and is written as (k₁ k₂ ... k_p ), where 1 < k₁, k₂, ... , k_p < n are distinct, if s (k) = k, k ¹ k₁, k₂, ... , k_p, s (k_i) = k_I+1, i = 1, 2, ... , p-1 and s (k_p) = k₁ . If p = 2, s is a transposition. If p is odd s is an even permutation and if p is even s is an odd permutation.

8. Two cyclic permutations (k₁, k₂, ... , k_p) and (l₁, l₂, ... , l_q) are called disjoint if k_i ¹ l_j for all 1 < i < p and 1 < j < q. Show that any two disjoint cyclic permutations commute and that any permutation s Î S_n can be written as a product of disjoint cyclic permutations.

A ring R is a non-empty set (denoted by R itself) with two binary operations, called addition (+) and multiplication (× ) such that

(a) (R,+) is a commutative group.

(b) The multiplication operation is associative (i.e., a× (b× c) = (a× b)× c, a, b, c Î R).

(c) The multiplication operation is distributive over the addition operation: For a, b, c Î R, a× (b+c) = a× b + a× c (left distributivity), & (b+c)× a = b× a + c× a (right distributivity).

The ring R is called commutative if the multiplication operation is commutative, i.e., ab = ba for all a, b Î R (Here, as is a common practice, "." signifying a multiplication is omitted).

The simplest example of a commutative ring is the set Z of all integers {0, ± 1, ± 2, ... } with the usual addition and multiplication (Q, R, C are also such examples). The subset of Z consisting of all even integers is also a ring. The set C^{n´ n} of all complex n´ n matrices, with the operations of matrix addition and matrix multiplication, is a non-commutative ring. The subset P(A) of it, consisting of all polynomials in a fixed matrix A is a subring (a subset of a ring which itself is a ring under the same binary operations) that is commutative.

Let p be a positive integer. Consider the set Z_p = {0, 1, 2, ... , p-1}, endowed with the binary operations of "addition modulo p" and "multiplication modulo p", i.e., for m, n Î Z_p, m + n = (m + n) mod p and m.n = (mn) mod p, where q mod p for an integer q is the unique remainder from amongst 0, 1, 2, ... , p-1 when q is divided by p and the quotient is kept as an integer. It is easily verified that Z_p is a commutative ring.

For a ring R, 0 ¹ a Î R is called a left zero divisor if there exists a 0 ¹ b Î R such that ab = 0 (b is then a right zero divisor). In a commutative ring the two notions of left and right divisors of 0 coincide and we call them just as zero divisors. A commutative ring without zero divisors is termed an integral domain. Thus (Z_p,+,.) is an integral domain.

An ideal S in a commutative ring R is a subring such that rs Î S for all r Î R and s Î S. If R is not commutative a subring S is a right ideal if sr Î S for all r Î R and s Î S and a left ideal if rs Î S for all r Î R and s Î S. If S is both a left and a right ideal it is called a two-sided ideal or simply an ideal. S is called proper if S ¹ R. An ideal generated by a subset S of a ring R is the smallest ideal of R containing S.

An ideal generated by a singleton element is called a principal ideal. An integral domain in which every ideal is a principal ideal is called a principal ideal domain. An ideal is called a maximal ideal if it is contained in no larger ideal than itself.

1. Characterize (i.e., figure out completely) all subrings of the rings Z, Q, R, and C.

2. If I is an integral domain having only a finite number of elements, show that (I\{0}, .) is a group.

3. For any a Î Z_p, show that pa = 0.

4. Find all the ideals in: (a) the ring Z of integers, & (b) the ring R of real numbers.

5. Show that Z is a principal ideal domain.

6. Show that the set C[a,b] of all real valued continuous functions on a closed interval [a,b] is a commutative ring under the ordinary addition and multiplication of functions.

7. Is the set of continuous functions from an interval [a,b] to itself a non-commutative ring under the ordinary addition and composition of functions ((f ° g)(x) = f(g(x))) as multiplication?

8. Prove that an intersection of ideals in a ring is an ideal.

9. Show that the ideal generated by a set S is the intersection of all ideals containing S.

10. Let S be a closed subset of [a,b]. Show that the set S of all functions f in C[a,b] that vanish on S is an ideal in C[a,b]. Is it true that all ideals in C[a,b] arise in this way?

11. Determine all principal ideals in C[a,b].

12. Is C[a,b] an integral domain?

A field F is a commutative ring in which every non-zero element has a multiplicative inverse. Thus (F,+) is a commutative group and if 0 denotes its zero element then (F\{0},× ) is a multiplicative group and the multiplication operation is distributive over the addition operation. In short, the addition and multiplication operations in a field F satisfy the ordinary rules of arithmetic, postulated as follows: For any a, b, c Î F,

1. a+b is a uniquely defined element of F;

2. a+b = b+a;

3. a+(b+c) = (a+b)+c;

4. There exists a unique element, written as 0, in F, such that a+0 = a;

5. Corresponding to b there exists a unique element written as "-b", in F such that b+(-b) = 0;

6. ab is a uniquely defined element of F;

7. ab = ba;

8. a(bc) = (ab)c;

9. There exists a unique element, written as 1 in F, such that 1a = a;

10. Corresponding to every c ¹ 0 in F there exists a unique element, written as c^-1, such that cc^-1 = 1.

11. a(b+c) = ab + ac. (Distributivity)

The sets of rational numbers Q, real numbers R, complex numbers C are fields with respect to the operations of ordinary addition and multiplications. These are examples of infinite fields, i.e., fields having an infinity of elements.

A subfield G is a subset of a field F such that with respect to the operations '+' and '.' of F, G in itself is a field. Clearly, G Ì F is a subfield iff 0, 1 Î G and it is closed under addition, multiplication, additive inversion and multiplicative inversion of non-zero elements. Thus if G is the set of real numbers of the form a+bÖ 2 where a, b are rationals, since (a+bÖ 2)^-1 = (a-bÖ 2)/ (a² -2b²), it follows that G is a subfield of R. If G is a subfield of F, F is called a superfield or an extension of G. If G is a subfield of a field F and if there exists a subset B of F possessing the property that each f Î F can be uniquely expressed as a finite sum S g_j b_j , where g_j 's belong to G and b_j 's to B, the cardinality of B is said to be the order [F:G] of F over G. (Later it will be seen that the order of F over G is simply the dimension of F regarded as a vector space over the field G and that the notion is independent of any particular such B.)

It is easily verified that the ring Z_p is a field iff p is a prime. Thus, with p prime, Z_p is an example of a finite field. Note that for any a Î Z_p , pa = 0.

A field is said to be of characteristic p ¹ 0, if p is the smallest positive integer such that pa = 0 for all a Î F. If no such integer p exists F is said to be of characteristic 0. If the characteristic p ¹ 0, one says that the field is of a finite characteristic. One has to be careful in working with a field of finite characteristic (e.g., from a = -a, in Z₂, one cannot conclude that a = 0!). We abbreviate the characteristic of a fild F by ch(F).

Theorem. If F is a field of a finite characteristics p, F^p = {x^p : x Î F} is a subfield of F, and h : x ® x^p is an isomorphism of F onto F^p.

Proof: Note that the charateristic p must be a prime, for if p = mn, with 1 as the unity of F we have 0 = p.1 = (m.1)(n.1) so that one of m.1 or n.1 equals 0, and if k.1 = 0, for any x Î F, k.x = k.(1x) = (k.1)x = 0x =0, contradicting the minimality of p. Since p | ^pC_j, 1 < j < p-1, (x+y)^p = x^p + S _{1£ j£ p-1} ^pC_jx^p-jy^j + y^p = x^p+y^p, and, of course, (xy)^p = x^py^p. Moreover, similar to the above x^p–y^p = (x-y)^p, implying that h is 1-1 and completing the proof. #

Corollary. If F is a finite field of a finite characteristic p, the map h : x ® x^p is an automorphism of F (i.e., isomorphism of F onto itself).

Proof: If F is finite, as sets F^p = F and the result follows. #

1. If F is a field, and if a , b , g Î F, then: (a) –0+a = a ; (b) If a +b = a +g , then b = g ; (c) a + (b -a ) = b. (b -a º b + (-a )); (d) a .0 = 0.a = 0; (e) (-1)a = -a ; (f) (-a )(-b ) = a b ; (g) If a b = 0, then a = 0 or b = 0

2. If a field is of characteristic p ¹ 0, p must be a prime.

3. Q, R, C are fields of characteristic 0, while Z_p (with p a prime) is of characteristic p.

4. Prove that Q, the field of rationals, is a subfield of every subfield of the field of complex numbers.

5. The only subfield of Z_p is Z_p itself.

6. Two fields F and F' are said to be isomorphic if there exists a 1-1 onto map h : F ® F' such that h (a +b ) = h (a ) + h (b ) and h (a b) = h (a )h (b ) for all a , b Î F. If F and F' are isomorphic with the isomorphism h , show that h (0) = 0 and h (1) = 1, where 0 and 1 commonly denote the zero and the unity of F and F'.

7. If F is a field of characteristic zero, show that F has a subfield isomorphic to the field Q of rational numbers. (One says that F contains a copy of Q).

8. Let F Ì G Ì H be fields. Show that [H:F] = [H:G][G:F].

9. Let q Î Q, the field of rational numbers. Prove that the set Q(Ö q) = {x+yÖ q : x, y Î Q} is a subfield of R iff x² = q is not solvable in Q (i.e., there is no x Î Q satisfying the equation).

10. Let F be a set which contains exactly two elements, 0 and 1. Define an addition and multiplication by the tables:

+ 0 1 × 0 1

Verify that the set F, together with these two operations, is a field. Is this field isomorphic to Z₂?

11. Prove that the set of 2´ 2 real matrices under the operations

is a field and that the map h : a + ib ® defines an isomorphism between C and this field.

12. In a field F, changing origin to a and then scaling up by a (¹ 0) in F corresponds to an invertible transformation f : F ® F, given by f (x) = (x-a)a . Show that Ff = (F, Å , Ä ), where xÅ y = f ^-1(f (x)+f (y)), xÄ y = f ^-1(f (x)f (y)) is a field and that h : F ® Ff given by h (x) = x is an isomorphism between the fields F and Ff . What are the 0 and 1 in Ff ?

13. Does R, the set of all ordered pairs (a,b) of real numbers, with addition and multiplication defined by: (a,b) + (c,d) = (a+c,b+d), and (a,b)(c,d) = (ac,bd), constitute a field?

14. Let F be a field. Is F´ F, with addition and multiplication defined by(a,b)+(c,d) = (a+c,b+d) and (a,b)(c,d) = (ac-bd,ad+bc) a field? Does the special case F = R have some extra significance?

15. Is the set F = {a,b,c}, with + and ´ defined below a field?

+ a b c ´ a b c

16. Find a finite field having proper subfields, if possible.

17. Show that the fields E Ì F Ì G have the same characteristic.

18. Does the set {0, ± 1, ± w , ± w ²}, where w is the cube root of unity, become a field with respect to ordinary addition and multiplication of complex numbers?

19. Can you list the subfields of Q? What about R? What about the subfields of C containing R?

20. Does the set of all polynomials with integer coefficeints form a field? What if the coefficients are allowed to be real numbers? What about the set of rational functions with integer coefficients? What about the set of rational functions with real coefficients?

21. Do complex rationals {s+it : s, t Î Q} form a subfield of C?

22. Let S = {z = x +ih : x , h Î [0,1)}, the semi-closed square. For z Î C, let z = z (mod S) denote the unique element in S such that the real and the imaginary parts of z-z are both integers. Define Å , Ä over C by zÅ z' = z+z' (mod S) and zÄ z' = zz' (mod S). Is S a field under Å , Ä ?

23. If a, b Î F, a field, verify that: (i) 0a = (0+0)a = 0a+0a Þ 0a = 0; (ii) 0a = (1+(-1))a = a + (-1)a Þ (-1)a = -a; & (iii) -b-a = -(a+b) = (-1)(a+b) = -1a+(-1)b = -a-b. Hence, deduce that the commutativiy of addition in F is a consequence of the other field axioms.

A vector space (V, +, .) over a field F is a set V, in which + : V´ V ® V (addition) and . : F´ V ® V (scalar multiplication) are such that (V, +) is a commutative group, and there hold: (i) 1.v = v, (ii) a.(b.v) = (ab).v, (iii) (a + b).v = a.v + b.v, and (iv) a.(u + v) = a.u + a.v, (a, b Î F, u, v Î V).

The most familiar example of a vector space over the field of real numbers is that of the Euclidean 3-d vectors v = xi + yj + zk, where i, j, k are the standard unit vectors in the positive directions of the x-, y- and z-axes and x, y, z are reals. In this case, in addition to vector addition and scalar multiplication, we also have the scalar, dot or the inner-product: v₁ .v₂ = x₁ x₂ + y₁ y₂ + z₁ z₂ , and the vector or the cross product

v₁ ´ v₂ = (y₁ z₂ –z₁ y₂ )i + (z₁ x₂ –x₁ z₂ )j + (x₁ y₂ –y₁ x₂ )k = .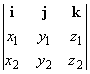

If V is a vector space over a field F, v₁ , v₂ , ... , v_n Î V and c₁ , c₂ , ... , c_n Î F, the vector v = c₁v₁ + c₂v₂ + ... + c_nv_n is called a linear combination of the vectors v₁ , v₂ , ... , v_n. The vectors v₁ , v₂ , ... , v_n are called linearly independent if the combination v = 0 only if the coefficients c₁ , c₂ , ... , c_n are all zero. Vector spaces will be taken up in greater detail later on.

A linear algebra, vector algebra or simply an algebra (A, +, ´ , × ) over a field F is a vector space (A, +, × ) over F, with the additional binary operation ´ : A´ A ® A such that (A, +, ´ ) is a ring satisfying c.(u´ v) = (c.u)´ v = u´ (c.v), (c Î F; u, v Î A).An algebra A is called a commutative algebra if the vector product operation "´ " is commutative: u´ v = v´ u, (u, v Î A). An algebra A is called an algebra with identity if there exists an element, say, 1 Î A, such that 1´ u = u, (u Î A).

1. Prove that every field F is a vector space over itself (with the operations "+" and "." being the same as those in the field (F, +, .)).

2. Prove that every field F is also a commutative algebra with identity over itself (with the operations "+" and "." being the same as those in the field (F, +, × ) and "´ " being the same as "× ").

3. Prove that, under the usual operations, C[a,b], the space of real valued continuous functions over the interval [a,b] is a commutative algebra with identity. What about the following spaces: C^m [a,b] of m-times continuously differentiable functions on [a,b], C¥ (R) of infinitely differentiable functions on the real line, A(D) of functions analytic in the unit disc and E the space of entire functions.

4. Prove that in the vector space R of real numbers over the field Q of rational numbers, the vectors 1 and x are linealy independent iff x is an irrational. What about the vectors 1, x and x ²? When are the vectors 1, x , x ², ..., x ⁿ linearly independent?

Let F be a field and x a symbol, or the so-called indeterminate. An expression of the type P(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ + ... = S _{0£ k<¥} a_kx^k, where a_k Î F and x^k, called the k-th power of x (in the sense of x.x.x ... x, k-times), is called a formal power series over the field F, or in short just a power series. It reduces to a polynomial in x over F, if all but a finite numer of a_k 's are zero. A polynomial S _{0£ k<¥} a_kx^k is said to be of degree n if a_n ¹ 0, while for all j > n, a_j = 0. A polynomial, written as P_n(x) = S _{0£ k£ n} a_kx^k, is of degree £ n, and it is of degree n if a_n ¹ 0. If P_n(x) is of degree n and a_n = 1, the unity (or the multiplicative identity) of F, we say that P(x) is a monic polynomial of degree n. A polynomial P(x) =S a_kx^k is called a non-zero- or a non-trivial- polynomial if at least one a_k is non-zero. One calls a_k as the coefficient of x^k, or the k-th coefficint of the polynomial.

The operations of addition "+", multiplication "´ " and scalar multiplication "× " for polynomials are defined, respectively, as:

S a_kx^k + S b_kx^k = S (a_k + b_k)x^k, (S a_kx^k)´ (S b_kx^k) = S S (a_jb_k-j)x^k, c.( S a_kx^k) = S (ca_k)x^k.

It is clear, from the definitions, that

deg (P + Q) £ max {deg P, deg Q},

deg (c∙P) = deg (P), (0 ¹ c Î F),

deg (P ´ Q) = deg P + deg Q, (P, Q ¹ 0),

i.e., the degree of a sum does not exceed the maximum of the degrees of the summands, the degree of a non-zero scalar multiple does not change and that the degree of a non-zero product equals the sum of the degrees of the factors.

Denoting the set of polynomials over a field F by F[x], we readily see that F[x] is a vector space over F (under + and .) and a ring (under + and ´ ). This may be summarized by saying that F[x] is an algebra over F. F[x] is called the linear algebra or the algebra of polynomials over F.

The notion of treating 'x' in a polynomial P(x) as a 'symbol' or as an 'indeterminate' could be formalized as follows: Consider the vector space P over a field F, of infinite sequences P = (a₀, a₁, a₂, ... , a_k, ... ) with a_k Î F, k = 0, 1, 2, ... , such that all but a finite number of a_k 's are zero, with addition and scalar multiplication defined component wise. If n is the largest index such that a_n ¹ 0, we identify P with a polynomial of degree n. Two polynomials are equal iff they are identical, the sum and scalar product for them are as in the vector space and defining the product P´ Q of P = (a₀, a₁, a₂, ... , a_k, ...) and Q = (b₀, b₁, b₂, ... , b_k, ...) as R = (c₀, c₁, c₂, ... , c_k, ...), where c_k = S a_jb_k-j, k = 0, 1, ... , we find that in the identification of P with the terminating power series or the polynomial P(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ + ... , the operations +, ., and ´ for P's and P(x)'s are consistent, with respect to which P is an algebra over F. With this clarification or understanding, we revert to our familiar notion of a polynomial as a polynomial P(x) in x. (If one wishes to formalize h : P ® F[x], defined by h ((a₀, a₁, a₂, ... , a_k, ...)) = S a_kx^k is an algebra isomorphism (1-1 onto map preserving algebra operations: h (P+Q) = h (P) + h (Q), h (cP) = ch (P), & h (P´ Q) = h (P)´ h (Q)).

1. For a Î F, prove that there holds the binomial expansion (x+a )ⁿ = S _{0£ k£ n} ⁿC_kx^{n-ka k} , n = 0, 1, 2, ... , where xa is a colloquial way of writing a x (also in the sequel).

2. If P(x) and Q(x) are polynomials and a Î F, such that P(x) = (x-a)Q(x) + R(a), prove that there holds R(a) = P(a).

3. If P(x) and Q(x) are polynomials and a, b Î F, such that P(x) = (x² + ax + b)Q(x) + R(a,b)x + S(a,b), develop a scheme for computing the scalar functions R and S. When F = R, also develop schemes for obtaining partial derivatives of R and S with respect to the variable a and b.

4. Prove that every ideal in the ring F[x] is principal.

5. Find the monic generator of whichever of the following subsets of Q[x] (Q - rational field) is an ideal: (a) all polynomials in x^k for some k £ 1; (b) all polynomials of degree ³ k for some k > 1; (c) all polynomials F such that f(Ö 2) = 0; (d) all polynomials F such that f(-1) = f(1) = f(0) = 0; (e) all indefinite integrals of polynomials defined by

, (ch(F) = 0).

6. Let A be an algebra over F and a Î A. Show that the set of all polynomials P in F[x] such that P(a) = 0 is an ideal.

7. If F Ì G are fields, show that an ideal J in F[x] and the ideal K in G[x] generated by J have the same monic generator.

The familiar algorithm (procedure) for the division of a non-zero polynomial Q(x) of degree m by another non-zero polynomial P(x) of degree n, produces a quotient polynomial q(x) of degree m-n and a remainder polynomial r(x) of degree < n such that Q = Pq + r, the result of which may formalized as :

Theorem (Remainder). Given two polynomials P and Q, there exist unique quotient and remainder polynomials q(x) and r(x) such that Q = Pq + r, where deg (r) < deg (P).

Proof: The existence of q and r follows from the division algorithm. For uniqueness, assuming that also Q = Pq¢ + r¢ , we have P(q-q¢ ) = r-r¢ , from which counting the degrees of the two sides we get the required contradiction. #

If Q = Pq, i.e., the remainder is zero, we say that P is a factor of Q or that P divides Q and symbolize it as P | Q. If P does not divide Q, we write P ł Q. Note that the zero polynomial can not divide any but the zero polynomial itself but that it is divided by every polynomial.

Example. Consider dividing Q = ax³ + bx² + cx + d, by P = x² + x + 1:

ax + (b-a)

x² + x + 1 ax³ + bx² +cx + d

ax³ + ax² +ax

(b–a)x² + (c–a)x + d

(b–a)x² + (b–a)x + (b–a)

(c–b)x + (d–b+a)

Here the quotient Q(x) equals ax+(b-a) and the remainder R(x) is (c-b)x+(d-b+a). It follows that the polynomial x² + x + 1 divides the polynomial ax² + bx + cx + d iff c = b = d+a.

1. If a polynomial P(x) is divided by x-a the remainder is P(a ) and x-a is a factor of P(x), iff P(a ) = 0.

2. Let p(x) = S ₀£ k£ n a_k x^k. Define its derivative by (Dp)(x) = p'(x) = S ₀£ k£ n ka_k x^k-1, and, with (D⁰p)(x) = p(x), the k-th derivative by (D^kp)(x) = D(D^k-1p)(x), k = 1, 2, ... . Show that if the field F is of characteristic zero, for any a Î F, p(x) = S ₀£ k£ n (D^kp)(a )(x-a )^k /k! (Taylor’s expansion). What happens if F has a non-zero characteristic?

3. Let x_i Î F, (i = 0, 1, 2, ... , n) be distinct. Let y_i Î F, (i = 0, 1, 2, ... , n). Define the so called fundamental Lagrange polynomials l_k(x) by l_k(x) = P ₀£ i£ n, i¹ k [(x_k –x_i )^-1(x-x_i )], k = 0, 1, ... , n, where the product has i going from 0 to n, without taking the value k. Verify that the polynomials l_k(x) possess the property l_k(x_j ) = d _kj, where (the Kronecker delta) d _kj equals 1 Î F if k = j, and 0 Î F, if k ¹ j and deduce that the polynomial L_n(x) = S ₀£ k£ n y_kl_k(x) (called the Lagrange interpolation polynomial corresponding to data points x_k‘s and data values y_k’s) interpolates the data in the sense that L_n(x_k) = y_k, 0 £ k £ n. Also prove that if P(x) is a polynomial of degree £ n and P(x_k) = y_k, then P(x) = L_n(x).

Let I denote an index set. The HCF (highest common factor) of a collection S = {Pa : a Î I} of polynomials over a field F is defined to be a monic polynomial of highest degree that divides each Pa . The HCF is also known as the GCD (greatest common divisor). The HCF of a string of polynomials P, Q, ... , R is denoted by (P, Q, ... , R), i.e., with the polynomials placed within the small brackets. An HCF exists since at least the monic polynomial 1 divides each polynomial and if a polynomial p divides all those in a set S, the degree of p does not exceed that of any P in S. Polynomials P, Q, ... , R are called relatively prime if (P, Q, ... , R) = 1.

Lemma (HCF). For any non-zero polynomial P and Q, their HCF (P,Q) is unique and is characterized by the propery that (P,Q) is monic and q | P, Q Þ q | (P,Q) for any polynomial q. Moreover, there exist polynomials R and S such that (P,Q) = PR + QS.

For some polynomials Q_i+1, in at most m £ deg P₀ steps we arrive at P_m = 0. Then P_m-2 = P_m-1 Q_m-1. It follows from the defining relations for P_k's that P_m-1 | P_m-2, P_m-3, …, P₂, P₁, P₀, and moreover that P_m-1 = P₀ r + P₁ s, for some polynomials r and s. Hence, if any polynomial q divides both P₀ and P₁ , it follows that q | P_m-1 . Choosing c Î F such that cP_m-1 is monic, the theorem as well as that (P,Q) = cP_m-1 is clear now. #

6. If P_i , 1 £ i £ k, are relatively prime so are the polynomials Q_i 's defined by Q_i = (P ₁£ j£ k P_j )/P_i , 1 £ i £ k.

7. If a, b Î F and a ¹ b, show that x-a and x-b are relatively prime.

8.Find the HCF of each of the following subsets of Q[x]: (a) (x-a)(x-b), x²-(b-a)x-ab}; (b) 1+x+x², 1+2x+2x² +x³, x³-1; (c) 1+x+2x²+3x³ , x³ +x²+2x+3; (d) x⁴ -4x³ -8x² -16x-48, x³ +12x² +28x+8; (e) xⁿ -1, n ³ 10.

A polynomial P(x) over a field F is called irreducible if no polynomial of a lower positive degree divides it, i.e., is a factor of it. A polynomial which is monic and irreducible is called a prime polynomial. (Recall that a positive integer is called prime number if it is not divisible by any smaller positive integer other than 1).

Proof: Suppose P ł Q. Then (P,Q) = 1, as P is a prime. Hence there exist polynomials p, q such that 1 = pP + qQ. But then P | pPR + qQR = R, as P | QR. #

Theorem (Prime Factorization). If P is a monic polynomial of a positive degree, there exist distinct prime polynomials p₁, p₂, ... , p_k, k ³ 1, and positive integers n₁, n₂, ... , n_k such that

Theorem (Chinese Remainder). If p₁, p₂, ..., p_k Î F[x] are relatively prime and r₁, r₂, ..., r_k Î F[x], there is a p Î F[x] such that p = r_i mod p_i , 1 £ i £ k.

Proof: Putting q_i = (P ₁£ j£ k p_j)/p_i , 1 £ i £ k, the q_i 's are relatively prime. (This is because otherwise there is a prime polynomial q dividing each of the q_i 's and so at least one of p_j 's. But then the polynomial q would fail to divide the corresponding q_j, a contradiction). Since (p_i ,q_i) = 1, there exist p_i¢ ,q_i¢ such that p_i¢ p_i + q_i¢ q_i = 1, 1 £ i £ k. Now, taking p = S ₁£ i£ k r_iq_i¢ q_i , the result follows. #

1. List all the prime polynomials over the fields R and C.

2. What can you say about the prime polynomials over Z₂?

3. Obtain the prime factorizations of P(x) = x² + px + q, where p and q are integers, over the fields Q, R and C.

4. If h is a monic polynomial over a field F and (f,g) = 1, show that (fh,gh) = h.

5. If f and g are polynomials over an algebraically closed field F (i.e., a field in which any polynomial of a positive degree has a solution), show that (f,g) = 1 if and only if f and g have no common root. Is the result true if F is not algebraically closed?

6. Let D denote the differentiation operator on the space of polynomials over a field F, show that f has no repeated roots iff f and Df have no root in common.

7. If f, g, and h are polynomials over a field F and h ¹ 0, f is said to be congruent to g modulo h (written: f º g mod h) if h divides f-g. Show that the congruence modulo h is an equivalence relation on F[x], i.e., (i) it is reflexive: f º f mod h, (ii) it is symmetric: if f º g mod h, then g º f mod h, & (iii) it is transitive: if e º f mod h and f º g mod h, then e º g mod h.

8. If f º p mod h, and g º q mod h, show that: f + g º p + q mod h; fg º pq mod h; and f(p) - p(f) º f(f) - p(p) mod h.

9. If f, g, h, and p ¹ 0 are polynomials and f º g mod p, prove that h(f) º h(g) mod p and f(h) º g(h) mod p(h).

10. Let f, g, h be polynomials over a field F. Prove that whenever fg º 0 mod h, there holds either f º 0 mod h or g º 0 mod h iff h is irreducible.

11. Let x_i Î F, 0 £ i £ n, be distinct and let y_i Î F, 0 £ i £ n, be arbitrarily assigned. Show that the Lagrange interpolation polynomial L_n(x) for the data y_i 's at the nodes x_i 's is the unique polynomial of degree £ n such that L_n(x_i) = y_i , 0 £ i £ n. (Recall that it is given by L_n(x) = S y_i P [(x-x_j)/(x_i –x_j )].)

12. Prove the generalization of Taylor's formula: f(g) = S ₀£ k£ n (k!)^-1f^(k)(h)(g-h)^k, where f, g, and h are polynomials over a field F of characteristic 0 and deg f £ n.

13. A polynomial P Î F[x] of degree n cannot have more than n roots counted after multiplicities.

14. Let F Ì G be fields and P, Q Î F[x]. Verify that the HCF’s of P and Q in F[x] and G[x] are the same.

The polynomial equation x² + 1 = 0, admits no solution in the field R of real numbers. On the other hand C, the field of complex numbers, which is a super field of R does contain the two solutions x = i and x = -i of the above equation. Equivalently, with respect to (over, or in the field) C, the polynomial x² + 1 factors completely (into a product of linear terms) as (x + i)(x - i). In analogy with the above example we ask the following question: given a polynomial P(x) in a field F, does there exist a field G É F such that P(x) is a product of linear factors in G? If so, G is called an extension of F in which the polynomial P(x) splits completely.

A field is algebraically closed if every polynomial in it is a product of linear factors. The fundamental theorem of algebra (proved with the help of analytic function theory) asserts that the field C of complex numbers is algebraically closed. In fact any field can be imbedded in an algebraically closed field. For most of our purposes it would be sufficient if starting from a field F and a polynomial P(x) in it we could pass to a super field of F in which P(x) splits:

Theorem. Given a field F and an irreducible polynomial p(x) over F, there exists a field F_p containing F in which p(x) is a product of linear factors.

Proof: Let deg p(x) = m. If m = 1, we have nothing to do. Else, consider the set P_m-1 of polynomials in an indeterminate l of degree £ m-1, with the coefficients in F. Equip P_m-1 with the usual addition, scalar multiplication, and multiplication modulo P(l ), which obviously turn it into an algebra over F . The ring P_m-1 would be a field if any 0 ¹ a(l ) Î P_m-1 could be shown to have a multiplicative inverse. For this, as p(x) is irreducible in F, we have the HCF, (p(x),a(x)) = 1. Hence there exist polynomials b(x) and Q(x) such that a(x)b(x) + p(x)Q(x) = 1. It follows that c(l ) Î P_m-1 such that c(x) = b(x) mod p(x) is the multiplicative inverse of a(l ). Thus P_m-1 is a field containing F in which, since p(l ) = 0 mod p(l ), l is a root of the polynomial p(x), i.e., (x-l ) is a factor of p(x). Thus p(x) splits in the field P_m-1 and if, by chance, p(x) splits completely in P_m-1 , we are through with F_p = P_m-1. Else, we continue iterating the above construction with any remaining irreducible non-linear factors of p(x), so that after at most m-1 such extensions we arrive at a required field F_p . #

Corollary. Any field F can be imbedded in an algebraically closed field G.

Proof: It uses Zorn's lemma in the usual fashion. Thus consider the set of all superfields of F partially ordered by inclusion. Any chain in it has an upper bound, namely the union of all the fields in the chain. It follows that there exists a maximal super field G, say, of F. If some non-linear polynomial in G is irreducible, by the previous theorem G could be further extended, contradicting the maximality of G. Hence G must be algebraically closed. #

Example. Taking F = R , p(x) = x²+1 and writing i for l , the construction in the proof of the previous Theorem gives rise to the field C of complex numbers a + ib, a, b Î R , which are polynomials over R of degree one in the indeterminate i. Fortunateley, C itself turns out to be algebraically closed (fundamental theorem of algebra); but a proof of it, however, involves complex analysis.

Another useful extension of a field F is to its field of fractions or rational functions Q_F = Q_F[x] in an indeterminate x. Its elements are quotients of polynomials P(x)/Q(x), where Q(x) ¹ 0, and two such quotients P₁/Q₁ and P₂/Q₂ are regarded as equivalent, or are identified, if P₁Q₂ = P₂Q₁. The addition and multiplication of two quotients are defined as P₁/Q₁+P₂/Q₂ = (P₁Q₂+P₂Q₁)/(Q₁Q₂), and (P₁/Q₁)(P₂/Q₂) = (P₁P₂)/(Q₁Q₂). The field F is imbedded in Q_F by the identification a = a/1, a Î F and it is easy to see that Q_F is a field with the above operations.

1. Prove that to every field F there corresponds a smallest algebraically closed superfield G.

2. Show that the field of fractions of Q_F[x] with the same indeterminate x coincides with Q_F[x] itself.

3. If F is a maximal field, what can you say about Q_F[x]?

5. Prove that x³+1 can be written as a product of linear factors over C , but not over R .