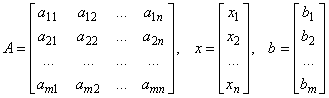 .
.Chapter 2
MATRIX THEORY
The basic purpose of matrix theory is to provide a systematic mechanism for solving a system of linear equations:
a11 x1 + a12 x2 + ... + a1n xn = b1,
a21 x1 + a22 x2 + ... + a2n xn = b2,
………………………………
am1x1 + am2x2 + ... + amnxn = bm,
This system has "m" equations in "n" unknowns x1, x2, ... , xn. The aij’s constitute the "matrix" A of the system, xi’s the "solution vector" x, and bi’s the "right-hand" or the "data vector" b, written, using matrix/vector notation, as
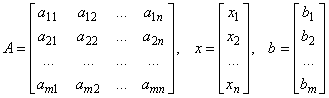 .
.
In the matrix/vector notation, the system of equations is abbreviated as: Ax = b. The definitions and operations on matrices/vectors that are introduced subsequently, make this equation not only symbolically but also mathematically meaningful.
Matrices
An m
´ n matrix A = (aij), 1 £ i £ m, 1 £ j £ n, is an abstraction of a rectangular arrangement of the m´ n entries aij into m-rows and n-columns: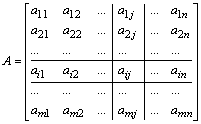 .
.
The entry aij occurring in the i-th row and the j-th column is called the (i, j)-th entry of the matrix A. By changing i one moves along the rows of the matrix and for entries in a particular row i remains constant. Similarly, varying j takes one to different columns of the matrix, j for all entries in a particular column being the same.
In general the entries in a matrix could be all kind of objects. If these objects come from a set S , we say that the matrix is over the set S . For definitive results in the sequel we shall mostly confine ourselves to matrices over certain structured sets (e.g., those of real and complex numbers, or polynomials etc.) which seem to us most useful.
The set of all m´ n matrices over a field F is denoted by F m´ n , F m,n or just F mn, if no confusion is caused. Those not interested in a general field F may, with a little loss and a possible ambiguity at places, assume F to be particularized to mean either the set R of real numbers or the set C of complex numbers with the standard operations of addition and multiplication (as well as subtraction and division) defined for them. A matrix over R is called a real matrix and that over C a complex matrix. A general m´ n matrix A is called a rectangular matrix, while if m and n equal, A is termed a square matrix of order n. An m´ 1 matrix is also called an m-component or m-dimensional column vector and a 1´ n matrix is called an n-component or n-dimensional row vector. Here the usage "n-component vector" is to be preferred over "n-dimensional vector" since the latter only refers to a property of the space the vector is coming from and not of the vector itself, whereas the n-components of the vectors are, of course, visibly clear. The set of all n´ 1 column vectors over a field F is simply denoted by F n (instead of the bulkier notation F n´ 1 ). The particular case C n is called the unitary n-space and R n, the Euclidean n-space. Similarly. we will denote the set of all 1´ n row-vectors over a field F by F (n). A sub-matrix of a matrix A is a matrix obtained from A by deleting a certain number of rows and columns from A.
As is the case with all mathematical objects, two matrices A and B are said to be equal, written A = B iff they are identical, i.e., of the same size and with the same respective entries.
PROBLEMS
1
. If A = B and B = C, verify that B = A and A = C (symmetry and transitivity of equality).2. Check if the total number of sub-matrices of an m´ n matrix is the odd number 2m+n – 2m – 2n + 1?
3. If the 3´ 4 matrix A of units of assets of three Stockists is given as per the table:
|
|
Item 1 |
Item 2 |
Item 3 |
Item 4 |
|
Stockist 1 |
10 |
4 |
8 |
2 |
|
Stockist 2 |
8 |
6 |
6 |
3 |
|
Stockist 3 |
15 |
8 |
4 |
4 |
and a commission agent buys/sells different items in rupees per unit of the items as given in the following 4
´ 2 matrix C in the table:|
|
Buying price |
Selling price |
|
Item 1 |
20000 |
22000 |
|
Item 2 |
15000 |
20000 |
|
Item 3 |
200000 |
240000 |
|
Item 4 |
300000 |
320000 |
verify that the profits the agent will get in buying and then disposing of the total assests of each of the three holders is given by the column vector t with components calculable according to the formula
ti =
S 1£ j£ 4 aij (cj2 – cj1 ), 1 £ i £ 3.If all the holders wish to sell their entire assets while the agent can purchase the assets of only one holder, which one should he approach to make a maximum percentage of profit on his investment?
4. Show the number of p
´ q sub-matrices of an m´ n matrix is [m! n!]/[(m-p)!(n-q)!p! q!] = mCp ´ nCq.
Matrix Addition
If A and B are two m
´ n matrices over a field F , their addition or sum matrix A+B is defined as an m´ n matrix C written as C = A + B, whose (i, j)-th element cij is given by: cij = aij + bij, 1 £ i £ m, 1 £ j £ n. The difference E = A - B of two matrices A and B is defined similarly (i.e., by: eij = aij – bij , 1 £ i £ m, 1 £ j £ n). Note that a zero matrix (i.e., a matrix with all entries 0) added to, or subtracted from, a matrix does not change it and that this property is enjoyed only by the zero matrix.Negative of a matrix A, written -A, is the matrix the (i, j)-th entry of which is -a , the negative of the corresponding entry in A. It follows that A - B = A + (-B).
Example. ![]() .
.
PROBLEMS
1
. For matrices over a field, verify that A+B = B+A, known as the commutativity property of addition, and that A+(B+C) = (A+B)+C, the associativity property of matrix addition.2. Let the box X contain 10 white balls and 20 red balls and the box Y contain 25 red and 15 white balls. If the contents of X and Y are cleared into an empty box Z and we wish to know the number of white and red balls in Z, what is wrong with the following statements:
x = ![]() , y =
, y = ![]() , z =
, z = ![]() ?
?
If one wishes to keep x as it is, correct y and z so as to make sense.
3. Set up an xy-coordinate system. Let r1 denote the velocity of a river in the x-direction and r2 in the y-direction. Let the respective components of the velocity of a boat relative to the river be denoted by b1 and b2. Find the absolute velocity components v1 and v2 of the boat in the x and y directions. If one puts
r = ![]() , b =
, b = ![]() , v =
, v =![]() ,
,
find the relation between the vectors r, b and v. Can you express b in terms of r and v?
4. Let {Ak}k³ 1 denote a sequence of matrices. Discuss what meaning should be ascribed to the writing
B = A1 + A2 + ... + Aj-1 + Aj = S 1£ k£ j Ak?
What would you like to mean by an infinite sum
C = A1 + A2 + ... + Aj + ... = S k³ 1 Ak?
Could you imagine a situations where an infinite sum could be meaningful? Would an infinite sum be meaningful if the field under consideration is not a subfield of C ?
5. The stocks (in kilograms) of three milkmen are as follows:
|
|
Milk |
Butter |
Cheese |
Curd |
|
Milkman 1 |
110 |
14 |
18 |
28 |
|
Milkman 2 |
108 |
17 |
16 |
35 |
|
Milkman 3 |
115 |
18 |
14 |
41 |
If at the end of the day the stock position is according to
|
|
Milk |
Butter |
Cheese |
Curd |
|
Milkman 1 |
15 |
4 |
13 |
11 |
|
Milkman 2 |
8 |
7 |
11 |
17 |
|
Milkman 3 |
14 |
5 |
9 |
15 |
find the amounts of various items the milkmen sold during the day. What has the matrix subtraction to do with the calculations? Use matrix addition to verify that the items sold and the items remaining add up to the morning stocks.
6. Let the components of a force F in the x, y and z directions be denoted by F1 , F2 and F3, respectively, so that F may be represented as a row vector (F1, F2, F3). If G is another force and both F and G act on the same particle, what is the resultant force H on the particle. If the particle moves from the point P1 = (x1, y1 , z1) to the point P2 = (x2, y2, z2), find the work done by the forces F, G and the resultant H of F and G. What is the relation between these three works done?
7. If p is a positive integer pA is defined as: 1A = A, 2A = A+A, 3A = A + 2A and (p+1)A = A + pA, in general. We put 0A = 0 and -pA = p(-A). Verify that if p and q are any integers, (p + q)A = pA + qA, and that (pq)A = p(qA).
Matrix Multiplication
If A is m
´ n and B is n´ p, that is the number of columns of A equals the number of rows in B, their multiplication or product AB is defined as an m´ p matrix C, written C = AB, for which![]() .
.
Note that AB is an m´ p matrix and that in order for it to be defined the number of columns in A has to equal the number of rows in B. Moreover, the order in which A and B occur in AB is important.
Example: If 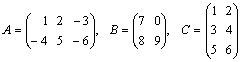 , out of the possible nine juxtapositions AA, AB, AC, BA, BB, BC, CA, CB and CC, the four products AA, AB, BC and CC are not defined, whereas the remaining five products AC, BA, BB, CA, and CB are defined and are given by
, out of the possible nine juxtapositions AA, AB, AC, BA, BB, BC, CA, CB and CC, the four products AA, AB, BC and CC are not defined, whereas the remaining five products AC, BA, BB, CA, and CB are defined and are given by
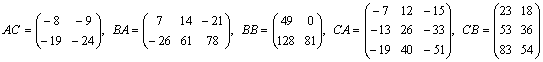 .
.
In a product AB, A is called the pre-multiplying and B as the post-multiplying matrix. Thus, AB is the pre-multiplication of B by A, or the post-multiplication of A by B.
If A = (aij ) is an m´ n matrix, the n´ m matrix B defined by bij = aji is called the transpose of the matrix A and is denoted by A¢ , Atr or At. If A and C are both m´ n we note that both the products A'B and BA' are defined and are respectively n´ n and m´ m matrices.
An n´ n matrix B for which bij = 0, if i ¹ j, and bii = 1 is called the n´ n identity matrix and is denoted by In. When the size n is understood from the context one drops n form In and writes it simply as I. Thus the symbol I commonly denotes identity matrices of various sizes. It is clear from the definition of matrix multiplication that IA = A and AI = A for any m´ n A, where the two identity matrices are respectively m´ m and n´ n.
PROBLEMS
1
. If x = Ay and y = Bz, is it true that x = (AB)z?2. Verify that the matrix multiplication is associative, i.e., A(BC) = (AB)C, (A l´ m, B m´ n, C n´ p). Construct examples to show that it is not commutative, in general, i.e., AB = BA does not hold for all n´ n A and B. Also prove that the matrix multiplication is both left and right distributive over the matrix addition, i.e., A(B + C) = AB + AC, (A m´ n, B, C n´ p) and (A + B)C = AC + BC, (A, B m´ n, C n´ p).
3. By now you can multiply two matrices and also know at least one situation where it could be useful. Can you imagine and interpret a case where you may need division of a matrix by another?
4. Let e = ad - bc ¹ 0. Let ![]() . Compute AB and BA. If x = Ay, show that y = Bx? If F is a matrix and z a vector such that Ay = Fz, find a matrix C such that y = Bz?
. Compute AB and BA. If x = Ay, show that y = Bx? If F is a matrix and z a vector such that Ay = Fz, find a matrix C such that y = Bz?
5. Find the number of distinct 2x2 matrices A ¹ 0, with entries 0 and 1 only that satisfy A2 = 0, where the field F under consideration equals (a) R , (b) C , (c) Z 2, & (d) Z 3.
6. Let A and B be 2x2 matrices such that AB = I. Prove that BA = I.
7. Prove that there exist matrices A and B such that AB - BA = ![]() , iff a + d = 0.
, iff a + d = 0.
8. If BA = A for all m´ n A, prove that B = Im and that if AC = A for all m´ n A, then C = In.
9. Since A(BC) = (AB)C, both the sides could be commonly represented as ABC. Then ABC could be evaluated in two ways. Similarly, (A(BC))D = ((AB)C)D = A((BC)D) = A(B(CD)) = (AB)1(CD)2 = (AB)2(CD)1 , where in the last product, e.g., the subscripts refer to the sequence in which the product is
formed and which is that first we evaluate CD and then AB and finally multiply AB with CD. All of these six equal products are commonly denoted by ABCD. Thus ABCD could be evaluated in six distinct ways. Give a similar meaning to the product A1A2A3 ... An-1An of n matrices and show that this product can be evaluated in precisely (n-1)! distinct ways.
10. Cite and discuss some physical situations where the matrix multiplication could be a useful tool in solving some problem.
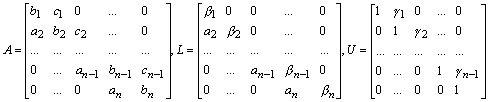
11. Consider the triadiagonal and the bi-diagonal matrices
 .
.
show that A = LU, where b 1 = b1, g 1 = c1/b 1; b j = bj –ajg j-1, j = 2, 3, ... , n, and g j = cj/b j, j = 2, 3, ... , n-1, provided that b j, 1 £ j £ n-1 are all different from zero. Further, show that the problem of solving the system of linear equations Ax = y gets transformed to that of solving the two related systems Lz = y and Ux = z, which, if none of the b j 's are zero, could be solved as follows:
z1 = y1/b 1, zj = (yj – ajzj-1)/b j, j = 2, 3, ... , n; xn = zn, xj = zj - g jzj+1, j = n-1, n-2, ... , 1.
12. If the n´ n matrices A, B commute, prove that the binomial expansion (A+B)m = S 0£ k£ m mCkAm-kBk, is valid. Construct examples of non-commutative matrices where (a) the expansion is valid, and (b) the expansion is not valid.
13. A matrix A = (a ) is said to be upper-triangular if aij = 0, whenever i > j. On the other hand, A is called lower-triangular if aij = 0, whenever i < j. Prove that the product of two upper triangular matrices is upper triangular and that of two lower triangular ones is lower triangular.
14. Entries in a matrix just below the main diagonal are said to constitute the sub-diagonal of the matrix. A square matrix in which every entry below the sub-diagonal is zero is called an upper-Hessenberg or just a Hessenberg matrix. Show that a product of a Hessenberg matrix and an upper triangular matrix is a Hessenberg matrix.
15. Banded matrices: A matrix A is called a (2k+1)-band matrix if aij = 0, whenever |i-j| > k. Thus a triadiagonal matrix is a 3-band matrix, a pentadiagonal matrix is a 5-band matrix and so on. Verify that the product of two triadiagonal matrices is a pentadiagonal matrix. Generalize to prove that the product of a (2k+1)-band matrix with a (2m+1)-band matrix is a (2[m+2k]+1)-band matrix.
16. If A is an n´ n upper triangular matrix, show that Ax = b is solvable for every b iff aii ¹ 0, 1 £ i £ n. What happens if A is lower triangular?
17. The obvious way of solving an upper triangular system (a system whose matrix is upper triangular) is known as the method of backward substitution. Similarly, for a lower triangular system (a system whose matrix is upper triangular) we may use the method of forward substitution. Use appropriate simplifications and backward/forward substitutions to solve the two systems:
x1 + 2x2 + 3x3 + ...………………………+ nxn = n2,
x2 + 2x3 + …………………… + (n-1)xn = (n-1)2,
……………………………………………………………..
xk + 2xk+1 + ... + (n-k+1)xn = (n-k+1)2,
………………………………………
xn-1 + 2xn = 4,
xn = 1;
and
z1 = n,
z1 + z2 = n-1,
z1 + z2 + z3 = n-2,
…………………………………………………………
z1 + z2 + z3 + …………………………+ zn-1 = 2,
z1 + z2 + z3 + …………………………+ zn-1 + zn = 1,
18. Positive integral powers of a square matrix are defined as follows: A1 = A, A2 = A1A = AA, A3 = A2A = AAA, and in general Ap+1 = ApA, where p is a positive integer. One puts A0 = I, the identity matrix of the same order as A. If there exists a matrix B such that BA = I, we define A-1 = B and A-p = (A-1)p . Thus Aq is defined for any integer q, where for negative q existence of the matrix B = A-1 is assumed. Show that if p and q are arbitrary integers, there hold: (i) Apq = (Ap)q, and (ii) Ap+q = ApAq.
19. Let A be a matrix with real entries. Suppose the matrices A2, A3, A4, ... are all having only positive entries. Is it necessary that A must also be a matrix of the same type?
20. Let A be a matrix with complex entries. If the powers A2, A3, A4, ... are all real matrices with all entries non-zero, is it necessary that A, too, is a matrix of the same type?
Scalar Multiplication
The Product of a matrix A by a scalar t is defined as the matrix C = tA where cij = taij, i.e., to get tA, each entry of A is multiplied by the scalar t. An m
´ m matrix B is called a scalar matrix if for some scalar c, bii = c and bij = 0, if i ¹ j. Thus a scalar matrix is a matrix of type cI, where I is an identity matrix. It is then easy to see that cA = (cI)A, i.e., scalar multiplying A by c is equivalent to pre-multiplying A by the scalar matrix cI, where I is m´ m if A is m´ n. Since (tIm)A = tA = A(tIn), often "At" is also used denote the scalar multiplication of A by the scalar t, and thus we have At º tA.Quite often one identifies a scalar s with the 1
´ 1 matrix (s); but then sA or As are not to be confused with the matrix products (s)A or A(s), which may not be defined at all. Indeed (s)A is defined iff A is 1´ n and then of course (s)A = sA. Similarly A(s) is defined iff A is m´ 1, and then A(s) = sA.
PROBLEMS
1. Let U denote an n
´ n matrix with 1's along the super-diagonal and 0's elsewhere: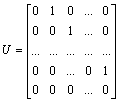 .
.
Compute U2, U3, ... , Un-1, Un. Hence, if I denotes the n´ n identity matrix (i.e., the matrix whose all diagonal elements are 1 and the off diagonal elements 0) and p = min{m, n-1}, show that
(l I+U)m = S 1£ k£ p mCk l m-k Uk.
2. Let A be m´ n, x is n´ 1 and b = Ax. Let Cj denote the n´ 1 vector with i-th component as aij. Cj is called the j-th column vector of A. Verify that b = S 1£ j£ n Cjxj = C1x1 + C2x2 + ... + Cnxn = S 1£ j£ n xjCj.
3. Let A be a 3´ 2 matrix. Prove that for whatever 2´ 2 matrix B there exists a 2´ 3 matrix C such that CA = B iff no column vector of A is a scalar multiple of the other.
4. Let A be a 2´ 2 matrix over a field F with ch(F ) ¹ 2. If A has only two distinct entries a and b both occurring twice and a + b ¹ 0, show that there exist two vectors v1 and v2 none of which is a scalar multiple of the other such that Avi = civi for some scalar ci, i = 1, 2. Moreover, show that if v ¹ 0 is any vector and c is a scalar such that Av =cv, then c = c1 or c = c2 and then: (i) if c1 ¹ c2 , v is a scalar multiples of v1 or v2 according as c = c1 or c = c2 and (ii) if c1 = c2 , v is a sum of scalar multiples of v1 and v2.
5. Prove that: (i) (a + b)A = aA + bA, (ii) (ab)A = a(bA), and (iii) a(A + B) = aA + aB. What names would you like to give to these laws?
6. Let A =![]() , x, y Î F 2, and c Î F . If Ax = cx, prove that cx = 0. If Ax = Ay = 0, show that x1y2 = y1x2. Arrive at the same conclusions if A =
, x, y Î F 2, and c Î F . If Ax = cx, prove that cx = 0. If Ax = Ay = 0, show that x1y2 = y1x2. Arrive at the same conclusions if A = ![]() .
.
7. If f(x) is a polynomial, A is an n´ n, B an n´ m and C an m´ n matrix over a field F and BC = I, the identity matrix show that f(CAB) = C[f(A)]B.
Block-Partitioned Matrices and Block Operations
By drawing horizontal and vertical lines across a matrix we get a partitioning of a matrix into blocks of sub-matrices such that the sub-matrices along the same row block have the same number of rows and those along the same column block have the same number of columns. Given such a configuration of a matrix A, we say that the matrix A has been given in a block-partitioned form or that A is a block-partitioned matrix. Thus if A is partitioned into p-row blocks and q-column blocks, the (i, j)-th block Aij, being a sub-matrix of A of size pi
´ qj , we write
If C1, C2, ... ,Cj, ... , Cn denote the column vectors of an m
´ n matrix A, the column partitioned form of A is as: A = [C1 | C2 | … | Cj | … | Cn]. The row partitioned form of A is defined analogously.Using the block-partitioned forms, the operations of addition, multiplication and scalar multiplication on matrices can be performed en-block. Thus, let A = (Aij) and B = (Bij) be two block partitioned matrices. Then, in the respective cases, assuming that sizes of A and B 's are compatible, in the block-partitioned form one has A+B = (Aij +Bij), AB = (
S k AikBkj), and a A = (aAij), where on the right hand sides is shown the (i, j)-th block of the matrices on the left hand sides. The compatibility in the above refers to the sizes of blocks being such that the sub-matrices Aij +Bij and AikBkj make sense. A verification of these is straightforward evaluation.
PROBLEMS
1
. Let B and C be real n´ n matrices and b, c, y and z real n´ 1 column vectors. Let A = B + iC, and for1 £ j £ n, aj = bj + icj, and xj = yj + izj. Verify that the n´ n complex system of equations Ax = a is equivalent to the 2n´ 2n real system of equations, written in a block partitioned form as:![]() .
.
2. If A = diag (A11,A22, ... ,Akk) is a block-diagonal n´ n matrix where the diagonal blocks Aii are square matrices and B is another n´ n matrix such that AB = I, the identity matrix, show that also the matrix B has the form diag (B11,B22, ... ,Bkk). Generalize the result for block triangular matrices.
3. Use partitioning to explicitly verify that the columns of AB are linear combinations of the columns of A and that the rows of of AB are linear combinations of the rows of B.
Vector Spaces of Matrices
With respect to the operations (+) (matrix addition) and (.) (scalar multiplication of matrices) the set
V = Fm´ n of m´ n matrices over a field F has the following properties:(1) For A, B
Î V and c Î F, A + B Î V and cA Î V. [V is closed under (+) and (× )].(2) A + B = B + A, for A, B
Î V.(3) A + (B + C) = (A + B) + C, for A, B, C
Î V.(4) There is a 0 (the zero matrix)
Î V, such that A + 0 = A for every A Î V.(5) For every A
Î V there is a -A (negative of A, i.e., the matrix whose every entry is the negative of the corresponding entry in A) Î V such that A+(-A) = 0.(6) 1.A = A, where A
Î V and 1 is the unity in F.(7) a(bC) = (ab)C, where a, b
Î F and C Î V (associativity with respect to scalar multiplication.(8) (a+b)C = aC+bC, where a, b
Î F and C Î V (distributivity of scalar multiplication over a scalar sum).(9) a(B + C) = aB + aC, where a
Î F and B, C Î V (distributivity of scalar multiplication over a vector sum).The vector spaces
Fn and F(n) of n-componet column and row vectors, respectively, are simply the vector spaces Fn´ 1 and F1´ n . More generally, in the sequel, a set V is called a vector space over a field F if there exist operations of vector addition + : V ´ V ® V and scalar multiplication • : F ´ V ® V for which (1)-(9) hold. A subset W of a vector space V which is closed under the operations of addition and scalar multiplication (i.e., + : W ´ W ® W and • : F ´ W ® W) is called a subspace of V.
PROBLEMS
1
. If W1 and W2 are subspaces of Fm´ n show that W = W1 Ç W2 is also a subspace. Also prove that W1 È W2 is a subspace iff one of W1 and W2 is contained in the other.2. Defining W = W1 + W2 = {w1 + w2 : wi Î Wi }, where Wi 's are subspaces of Fm´ n, show that W is a subspace of Fm´ n.
3. Show that the equation (W1 + W2 ) Ç W3 = W1 Ç W3 + W2 Ç W3 , is not necessarily true if Wi 's are subspaces.
4. Let W1 and W2 denote subsets of F2´ 2 of matrices of type ![]() and
and ![]() , respectively.
, respectively.
(i) Show that W1 , W2 , W1 Ç W2 and W1 + W2 are subspaces of F2´ 2.
(ii) Note that W1 and W2 are each described by three parameters (namely x, y, z and a, b, c) and that no two will do. Now find the number of minimal parameters that descibe W1 Ç W2 and W1 + W2 .
The Standard Inner Product In Rn and C n
Let
K denote any of the fields R or C . Consider the vector space K n over K . The sum S 1£ i£ n xiyi* = (x,y), where x = (x1,x2, ... ,xn)¢ , and y = (y1,y2, ... ,yn)¢ Î K n and y* denotes the complex-conjugate of y, is called the standard inner-product in K n. Note that when K = R , the complex conjugation is not required and we simply have (x,y) = S 1£ i£ n xiyi.
PROBLEMS
1
. Verify the following properties of the standard inner product: (i) (x,x) ³ 0 and the equality holds iff x = 0, (ii) (x+y,z) = (x,z)+(y,z), (iii) (cx,y) = c(x,y), (iv) (x,y) = (y,x)* .2. Show that the complex
l minimizing f(l ) = (x-l y,x-l y) is given by l = (x,y)/(y,y). Deduce that (x,y)(y,x) £ (x,x)(y,y). What if we minimize f(l ) with respect to a real l ?3. Let A be an m
´ n matrix, x Î Rn and y Î Rm . If (Ax,y) = 0 for all x and y, show that A = 0, the matrix with all zero entries.4. If for A = (aij), its conjugate transpose or adjoint A* is defined as the matrix whose (i,j)-th entry equals aji* , the complex conjugate of the (j,i)-th entry of A, prove that (Ax,y) = (x,A* y).
5. If A is a complex n´ n matrix and A* = A (i.e., A is self-adjoint), show that (i) (Ax,x) is real for all x Î ℂn, (ii) if for some l Î ℂ and 0 ¹ x Î ℂn, Ax = l x, then l Î ℝ and (iii) if Ax = l x and Ay = m y, where l ¹ m and x, y ¹ 0, then (x,y) = 0.
Linear Independence of Matrices
Let A1, A2, ... , Ak be m
´ n matrices over a field F. We call them linealy-dependent or simply dependent if there exist c1, c2, ... , ck Î F, not all zero, such that c1 A1 + c2 A2 + ... + ck Ak = 0, the m´ n zero-matrix. A finite or infinite set of matrices is called linearly dependent or dependent if a finite subset of it is dependent. A set S of matrices (and the members of it) are called linearly-independent if S is not linearly-dependent. It follows that if S is linearly-independent then A1, A2, ... , Ak Î S, c1, c2, ... , ck Î F and c1 A1 + c2 A2 + ... + ck Ak = 0 imply that c1 = c2 = ... = ck = 0.Linear dependence or independence of vectors in
Fn and F(n) is synonymous with their linear dependence or independence as elements of Fn´ 1 and F1´ n , respectively. The notion of linear independence in a general vector space is exaclty analogous, but will be taken up only later.
PROBLEMS
1
. Find three vectors in R 3 which are linearly dependent but are such that any two of them are linearly independent.2. Prove that the four vectors (1,0,0), (0,1,0), (0,0,1) and (1,1,1) in
R (3) form a linearly dependent set, but that any three of them are linearly dependent.3. Give an upper bound for the number of elements in a linearly independent subset of (i)
Fm´ n, (ii) the set of symmetric matrices in Fn´ n, (iii) the set of upper triangular matrices in Fn´ n and (iv) the set of diagonal matrices in Fn´ n. Is the upper bound sharp?4. For 1 £ i £ m and 1 £ j £ n, let Eij denote the m´ n matrix whose (i,j)-th entry is 1 and the remaining entries are all zero. Prove that the matrices Eij are linearly independent.
5. Prove that the row vectors of an n´ n upper triangular matrix A are linearly independent iff aii ¹ 0, 1 £ i £ n. Deduce that the column vectors of an n´ n upper triangular matrix A are linearly independent iff aii ¹ 0, 1 £ i £ n.
Some Standard Matrices
In the sequel, unless otherwise stated, elements of matrices will be scalars from a general field
F or ℝ (real line) or ℂ (complex plane). The square matrix I = (d ij), where d ij is the Kronecker-delta![]() ,
,
is called an identity matrix. (We have come across this matrix earlier.) Obviously IA = A, AI = A, where A is any m´ n matrix, the first I being m´ m and the second n´ n. A matrix all of whose entries are zero is called a zero or a null matrix.
A matrix B is called a left inverse of a matrix A if BA = I, an identity matrix. In this situation A is equivalently called a right inverse of B. Note that if A is m´ n, here, then B is n´ m. If AB = BA = I, B is called an inverse of A (and is written as B = A-1 ). Here A has to be a square matrix. Later we will see that in this case AB = I Þ BA = I. Moreover, an inverse, if it exists, will be seen to be unique. Also, the symmetry of the definition implies that if B is the inverse of A then A is the inverse of B. A matrix possessing an inverse is called an invertible or a non- singular matrix. If A-1 does not exist, A is called singular or non-invertible.
A square matrix is called a diagonal matrix if all entries above or below the main diagonal in A are zero. For a diagonal matrix D one writes D = diag(d1,d2,d3, ...,dn), where dii is the i-th diagonal entry of D. A matrix T is called upper triangular if entries in T below the main diagonal are zero. Similarly L is called lower triangular if entries in L above the main diagonal are all zero. An upper triangular matrix is called strictly upper triangular if also its diagonal entries are zero. Similarly, a strictly lower triangular matrix is a lower triangular matrix whose diagonal entries are also all zero.
A¢ º AT º At , called the transpose of matrix A = (aij), is the matrix A¢ = (aji), whose (i,j)-th element is the (j,i)-th element of A. Ā, called conjugate of a complex matrix A is the matrix whose (i,j)-th element is the complex conjugate of the (i,j)-th element of A. Thus Ā = (āij). The conjugate-transpose (sometimes, also called the adjoint) of a complex matrix A is the matrix A* º Ā¢ º (A¢ )-, obtained by conjugating the transpose, or equivalently, transposing the conjugate of the matrix A.
A matrix A is called symmetric if A = A¢ and skew-symmetric if A¢ = -A. A symmetric matrix with real entries is called a real-symmetric matrix. A is called hermitian if A* = A and skew-hermitian if A* = -A. A is called orthogonal if A-1 = A¢ , i.e. A¢ A = AA¢ = I. An orthogonal matrix with real entries is called real-orthogonal. A matrix is called unitary if A-1 = A* , i.e. A* A = AA* = I. Clearly, a real Hermitian matrix is symmetric and a real symmetric matrix is hermitian. Also, a real unitary matrix is orthogonal and a real-orthogonal matrix is unitary.
An m´ n A is called sub-unitary if A* A = I. Thus, a square sub-unitary matrix is unitary. Similarly, if A¢ A = I and A is m´ n, it is called sub-orthogonal (for m = n it becomes orthogonal). A sub-orthogonal matrix with real entries is called a real-sub-orthogonal matrix.
A matrix A with real or complex entries is called positive definite if x* Ax º S 1£ i£ nS 1£ j£ n aij (xi)-xj > 0, for every n´ 1 non-zero complex vector x. If x* Ax ³ 0 for all complex n´ 1 vectors x, A is called a positive semidefinite matrix. If -A is p.d. (positive definite), A is called negative definite (n.d) and similarly, if -A is positive semidefinite (p.s.d), A is called negative semidefinite (n.s.d).
Let A be a square n´ n matrix. The trace of A, written Tr A or tr A, is the sum of its diagonal entries: tr A = S 1£ i£ n aii. By changing the order of the double summation, one easily verifies that tr AB = tr BA, where A is m´ n and B is n´ m.
For a square A, (l ,x) is called an eigen-pair, l an eigen-value and x a corresponding eigen-vector of A if Ax = l x, and x ¹ 0, where l Î F, A is n´ n and x is n´ 1.
PROBLEMS
1
. Every real n´ n matrix A can be uniquely written as a sum of a real symmetric matrix and a real skew-symmetric matrix.2. Every complex n
´ n matrix A can be uniquely written as a sum of a Hermitian matrix and a skew-Hermitian matrix.3. Every diagonal matrix commutes with every other diagonal matrix.
4. If D is a diagonal matrix with distinct diagonal entries and A is a matrix such that DA = AD, then A is also a diagonal matrix.
5. If S is an n
´ n upper (lower)-triangular matrix (i.e., entries below (above) the diagonal are all zero) and UT = I, then T is an upper (lower)-triangular matrix. Moreover, the set of all upper (lower) triangular matrices is closed with respect to the operations of sums, differences and scalar, as well as, matrix products.6. Show that a diagonal matrix D = diag (d1,d2, ... ,dn) has an inverse iff none of di 's is zero. Moreover, if the inverse exists show that it is given by D = diag (d1-1,d2-1, ... ,dn-1).
7. Eigen-values of a triangular-matrix are its diagonal entries. (Prove.)
8. Prove that tr(ABC) = tr(BCA) = tr(CAB) and find couter examples for the other non-cyclic permutations.
9. Let A be a complex matrix (i.e., with complex entries). Prove that tr(A
* A) = 0 iff A = 0. Find an example of a matrix A ¹ 0, for which tr(A2) = 0.10. If A is p.d., can you prove that A is necessarily hermitian?
11. Prove that A*A is p.s.d. for every complex A and it is p.d. if Ax
¹ 0 for every x ¹ 0.12. A2, even for a real matrix A, need not be p.s.d., p.d., positive or even non-negative. Find examples to this effect.
13. If A and B are n
´ n matrices, AB = I implies that BA = I. Can you prove it? Construct examples to show that if A is m´ n and B is n´ m and m < n, it is possible that AB = I (the m´ m identity matrix) but that it is impossible that BA = I (the n´ n identity matrix).14. Prove that a 2
´ 2 matrix A =15. If D is a diagonal matrix with positive diagonal entries and A is a complex matrix such that D2 commutes with A, show that A commutes with D.
Elementary Row And Column Operations
The elementary row operations (EROs) on an m
´ n matrix A are of the following three types:(i) Multiplying i-th row by a non-zero scalar c.
(ii) Interchanging i-th and j (
¹ i)-th rows.(iii) Adding to i-th row a scalar c times j (
¹ i)-th row.The operations (i)-(iii) may, respectively, be denoted by cR , Ri
« Rj and Ri + cRj. It is easily seen that their effects are reversible (through the inverse elementary row operations c-1R , Ri « Rj and Ri - cRj, respectively).Let A and B be two m
´ n matrices. A is said to be row equivalent to B (A ~ B) if A can be obtained from B by performing a finite number of elementary row operations on B. It follows that the row equivalence is an equivalence relation on Fm´ n (i.e., A ~ A, A ~ B Þ B ~ A and A ~ B and B ~ C Þ A ~ C).A motivation for studying elementary row operations comes from systematizing methods for solving a system of linear equations and related questions. Consider, for instance the problem of determining when two m
´ n consistent systems Ax = b and Cx = d are equivalent. A consistent system means that itpossesses at least one solution, i.e., the solution set is non-empty. By equvalence of two consistent systems we mean that the two systems have exactly the same set of solutions.
Now, starting with a system Ax = b if we apply a succession of the following three types of operations: (1) multiplying both sides of the i-th equation by a non-zero scalar c; (2) interchanging i-th and j (
¹ i)-th equations; and (3) adding to i-th equation a scalar c times j (¹ i)-th equation, on the system we get another equivalent system. This is because all these operations are reversible and so if x satisfies the original system it satisfies the transformed one and vice versa. Note the similarity of these operations with the corresponding elementary row operations. Now the interesting result in this direction is the following converse: "Two consistent m´ n systems are equivalent only if one can be obtained from the other in this fashion, i.e., by a succession of the above three types of operations."Now, suppose Ax = b is an n
´ n system possessing a unique solution, given by xi = di, 1 £ i £ n, say. But this writing of the solution again constitutes a system of linear equations of the form Cx = d, with C as the identity matrix. Hence by the above equivalence it follows that the solution can indeed be obtained simply by an appropriate succession of the operations of type (1)-(3). This idea of Gauss leads us to the well-known "elimination method" for solving Ax = b : Use one of the equations to eliminate x1 from the remaining n-1 equations. Use one of the n-1 equations to eliminate x2 from the remaining n-2 equations, and so on till you eliminate xn-1 from the remaining 1 equation which would then contain only xn . This process is called forward elimination. The n-equations that you have after the forward elimination, are of type Ux = v, where U is an upper triangular matrix. Its solution can be found by the so-called back substitution, which consists in determining xn from the last equation, substituting for xn and determining xn-1 from the (n-1)-th equation, substituting for xn and xn-1 and determining xn-2 from the (n-2)-th equation, and so on till finally substituting for xn, xn-1, xn-2, ... , x3, x2 and determining x1 from the first equation.One more point: The m
´ n system Ax = b is characterized by the matrix A of the system and the right hand vector b. If we construct the m´ (n+1) matrix [A | b], whose first n columns are the columns of the matrix A and the last column is a copy of the vector b, the matrix [A | b] contains all information regarding the system Ax = b excepting for the dummy notation for the vector x, which is of no mathematical consequence anyway. This matrix [A | b] is called the augmented matrix of the system Ax = b. Using the notion of the augmented matrix, we see that if Ax = b is transformed into Cx = d by a succession of the operations (1)-(3), the corresponding operations (i)-(iii) applied on [A | b] convert it to [C | d]. That is why for studying a system Ax = b of equations, we could confine our attention to the augmented matrix [A | b] and the elementary row operations (i)-(iii). The studies subsequently reveal as to how to deal with the inconsistent systems, or the systems that do not possess a unique solution. For the present, we give the following definition: Two m´ n systems (consistent or not) Ax = b and Cx = d are called equivalent if one can be obtained from the other by a finite sequence of operations of type (1)-(3), or equivalently, if [A | b] and [C | d] can be obtained from each other by a succession of elementary row operations.Let A be m
´ n. Each of the above mentioned three elementary row operations (i)-(iii) on A corresponds to premultiplication of A by an m´ m matrix, obtainable by performing the same operation on an m´ m identity matrix. The respective pre-multiplying matrices for (i)-(iii) are thus: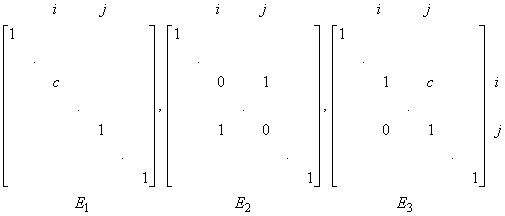 .
.
That the premultiplications by these E1, E2, E3 results in the indicated EROs (i)-(iii), is a matter of direct verification. Matrices of above three types are called elementary matrices.
In (i)-(iii) the word 'row' changed to 'column' results in the elementary column operations (ECOs). These in turn correspond to post multiplication by n´ n matrices:
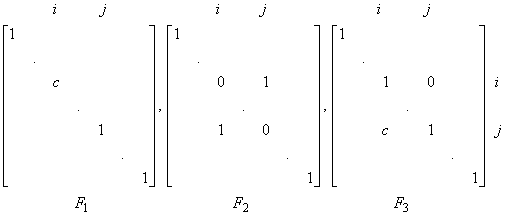 .
.
Note that in the column case, the matricesf F1, F2 in the cases (i)-(ii), excepting for their sizes, have the same structure while in (iii) in the column case we get F3 which is the transpose of the matrix E3 of the row case (iii).
PROBLEMS
1
. Are the following pairs of complex systems of linear equations equivalent? If so, express each equation in each system as a linear combination of the equations in the other system:(a) x1 - ix2 = 0, x1 + ix2 = 0,
x1 + x2 = 0, x1 + x2 = 0.
(b) x1 + x2 + x3 = 0, x1 + 2x2 + x3 = 0,
x1 - x2 + x3 = 0, 2x1 + x2 + 2x3 = 0.
x1 + x2 + x3 = 0.
(c) x1 + x2 + 0x3 + x4 = 0, 3x1 + 2x2 + ix3 - 2x4 = 0,
x2 - ix3 + 5x4 = 0, 5x1 + 4x2 + ix3 + 0x4 = 0.
2. For what choice of the parameter a are the following systems of linear equations over the field R consistent:
(a) x1 + x2 = 10, (b) x1 + x2 = 10, (c) a x1 + a x2 = 10,
a x1 + x2 = 20. a x1 + a x2 = 20. a x1 + a x2 = 20.
(d) x1 + x2 - x3 = 1, (e) x1 + x2 - x3 = 1,
x1 - x2 + x3 = 1, x1 + x2 + x3 = 1,
a x1 + x2 + x3 = 1. a x1 - x2 + x3 = 1.
3. Devise an algorithm (a general strategy, or procedure) for expressing (a) a non-singular n´ n matrix A and (b) its inverse A-1, as products of elementary matrices. The algorithm should fail iff A is singular. Practise the algorithm on the following matrices:
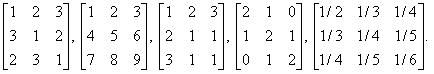
4
. Prove that the matrices E1, E2, E3 and F1, F2, F3 obtained by performing the elementary row and column operations (i)-(iii) on an identity matrix are invertible and find their inverses.
Row-Reduced Echelon Form
A matrix is said to be in a row-reduced echelon form if:
(i) no non-zero row succeeds a zero row, i.e., zero rows occur only at the bottom of the matrix.
(ii) the first non-zero entry in any non zero row is 1 (unity of the field, called a leading unity.
(iii) the column containing a leading unity has every other entry zero.
(iv) if leading unity in i-th row occurs in p(i)-th column p(1) < p(2) < …, i.e., {p(i)} is an increasing sequence.
It is clear that through elementary row operations (eros) any matrix could be reduced to a row-reduced echelon form: we start with the first column. If all entries in it are zero, we proceed to the next column and so on. If some entry in the column is non-zero, apply an interchange of rows to bring it to the top position and then divide this row by the non-zero entry to make the entry a leading unity. Next subtract
appropriate multiples of this row from every other row so that every other entry in the same column is zero. Continuing this process with subsequent columns and rows we end up, finally with a row-reduced echelon form.
Replacing the word 'row' by 'column' every in above, we get the so called column-reduced echelon form of a matrix, which can be realized through the elementary column operations.
In view of the equivalence of elementary row (column) operations with pre (post) multiplication by the corresponding elementary matrices, we immediately have:
Theorem. Let A be m
´ n. Then there exist non-singular m´ m B and n´ n C such that BA is in row-reduced echelon form and AC is in column-reduced echelon form.Theorem (Unicity of the row-reduced echelon form). Let A be an m
´ n matrix over a field. If B and C are non-singular and BA and CA are in row-reduced echelon forms, then BA = CA.Proof. The proof is by induction on m. When m = 1 the result is obvious. Thus assume the result for (m-1)
´ n matrices. Let E = BA and F = CA. Since B and C are non-singular and hence products of elementary matrices, each row of E can be obtained as a linear combination of rows of F and conversely. If E = 0, obviously F = 0 and conversely. If E ¹ 0, F ¹ 0, and let p denote the number of the column in E containing the leading unity of the first row and let let q denote the same for F. If p < q, the columns 1 to q-1 in F are zero. In particular the p-th column of F is zero and hence the first row of E can not be obtained from F by elementary row operations as the p-th column entry of the first row of E is non-zero. Similarly q < p is equally false and so p = q.Now the second onward rows of F can be written as linear combinations of the second onward rows of E, since if the first row of E is involved in the corresponding linear combination the p-th entry in the row would be non-zero, which would contradict the just established fact that the p-th column of F has each entry, excepting the one in the first row, zero. Similarly the second onward rows of E can be written as linear combinations of the second onward rows of F.
Thus, if E1 and F1 denote the matrices obtained from E and F, respectively, by deleting their first rows, then E1 and F1 are row-equivalent row-reduced echelon forms and hence, by the induction hypothesis for (m-1)
´ n matrices, are equal. In view of this the first rows of E and F are also to be the same, since no contribution can come from second onward rows of F while we are writing the first row of E as a linear combinations of the rows of F. Thus the result for m´ n matrices follows and the induction is complete. #Note that B in the above theorem is the product of the pre-multiplying elementary matrices which give rise to the row-reduced echelon form of A. Similarly, C is the product of post multiplying elementary matrices corresponding to the elementary column operations giving rise to the column-reduced echelon form for A.
Since the column-reduced echelon form of A is the transpose of the row-reduced echelon form of the transpose of A, it follows that the column-reduced echelon form of a matrix is also unique.
PROBLEMS
1
. Find all solutions ofo the following system of equations by row-reducing the coefficient matrix to its echelon form:x1 + 6x2 - 18x3 = 0,
3x1 - 6x2 + 13x3 = 0,
5x1 + 6x2 - 23x3 = 0,
7x1 - 6x2 + 8x3 = 0.
2. Find a row-reduced echelon matrix which is row-equivalent to: 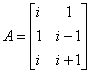 .
.
What are all the solutions of Ax = 0? If the last row of A is changed to something else, would it make a difference in the results?
3. Describe explicitly the possible forms of all 2´ 2 and 3´ 3 row-reduced echelon matrices. Do these forms depend on the field F under consideration?
4. Is the system of equations
x1 - 2x2 + 8x3 = 1,
x1 - 3x2 + 5x3 = 1,
x1 - 4x2 + 2x3 = 1,
consistent? If so, describe explicitly all solutions.
5. Show that the system
x1 - 2x2 + x3 + 4x4 = 1,
x1 + x2 - x3 + 2x4 = 2,
x1 + a x2 -5x3 - 2x4 = 3,
has no solution iff a = 7. If a ¹ 7, find the general solution?
6. Find all solutions of
x1 + x2 + 3x3 - 3x4 = 3,
x2 + x3 - x4 = -2,
4x2 + 4x3 - 4x4 - x5 = 7,
x1 -3x2 - 3x3 + 2x4 +x5 = 0.
7. Find the most general a, b and c if the system of equations
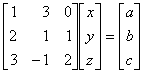
is to be consistent. What is the smallest number of parameters required to describe a, b and c?
8. Let 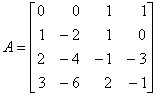 . What is the minimum number of parameters needed to represent the most general b if Ax = b is to be consistent? What is the minimum number of parameters required to describe z such that Az takes all possible values b that make Ax = b consistent?
. What is the minimum number of parameters needed to represent the most general b if Ax = b is to be consistent? What is the minimum number of parameters required to describe z such that Az takes all possible values b that make Ax = b consistent?
9. If A is an m
´ n matrix over a field F, prove that there exists an n´ m matrix B such that x = Bb is a solution of Ax = b, whenever b is such that the system Ax = b is consistent.10. If Ax = b is inconsistent, there exists a c such that Ax = c has more than one solution. True or false?
11. For a square matrix A over a field
F, the following statements are equivalent:(i) A is invertible.
(ii) The row (column) -reduced echelon form of A is I, the identity matrix.
(iii) A is a product of elementary matrices.
(iv) Each row (column) in the row (column) -reduced echelon form of A is non-zero.
12. For the block partitioned matrices
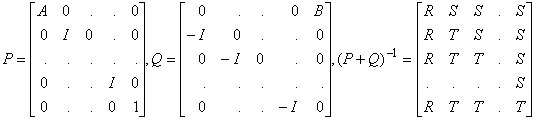
where R = (A + B)-1, S = -RB, and T = RA = I + S. If A + B is not invertible, could it be that P+Q is still invertible.
13. Prove that there are exactly two 2
´ 2 complex row-reduced echelon matrices the sum of all the four entries of which is 0.14. Prove that the interchange of two rows of matrix can be accomplished by a finite sequence of elementary row operations of the other two types. (Hint: Ri - Rj , Rj + Ri , Ri + Rj , -Ri).
15. Find all solutions of the system of equations: 2x1 + (1+i)x2 = 0, (1+i)x1 + ix2 = 0.
16. If 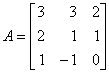 , find all solutions of Ax = 0 by row-reducing A to its echelon form.
, find all solutions of Ax = 0 by row-reducing A to its echelon form.
17. If 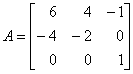 , prove that Ax =
, prove that Ax =
18. Find the row-reduced echelon form of the matrix 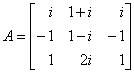 .
.
19. Verify that the following matrices are not row equivalent: 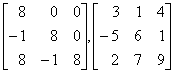 .
.
20. Find all solutions of the system of equations Ax = 0, where ![]() , when: (i) A = 0, (ii) A
, when: (i) A = 0, (ii) A