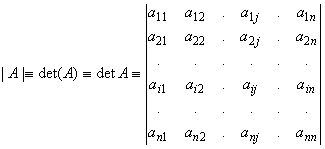 ,
,Determinant of a Square Matrix
A determinant could be thought of as a function from
Fn´ n to F: Let A = (aij) be an n´ n matrix. We define its determinant, written as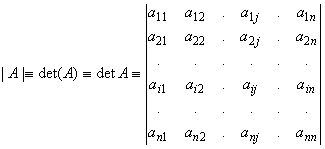 ,
,
by
![]() .
.
where Sn is the group of all n! permutations on the symbols{1,2,3,4,...,n} and sgn (s ) for a permutation s Î Sn is defined as follows: Let s written as a function be
![]() .
.
Let Ni (1 £ i < n) denote the number of indices j > i, for which s (j) < s (i), and let N(s ) = S 1£ i<n Ni. Ni is called the number of inversions in the permutation s corresponding to the index i, and N is called the total number of inversions in the permutation s . Finally, we define sgn (s ) by the relation sgn (s) º (-1)N(s ) . Thus, sgn (s ) is +1, or -1 according as N(s ) is even, or odd, and accordingly, we call the permutation itself to be even, or odd permutation.
The above notion of determinant remains useful in many more situations, e.g., when the entries of A are from a commutative ring G with identity (e.g, the ring F [x] of polynomials over a field F). In the sequel, however, unless otherwise specified we restrict to the case of matrices over a field.
Theorem. If A is a square block upper triangular matrix over a ring G, in which the diagonal blocks are square, then the determinant of A equals the product of the determinants of its diagonal blocks.
Proof: Suppose the n´ n A is partitioned into m2 blocks Apq, where Apq is square if p = q and Apq = 0 if p > q, 1 £ p, q £ m:

Let Sp denote the set of row or column numbers pertaining to the block App and let c(Sp) denote the number of elements in Sp. Consider the right hand side of
![]() .
.
If s Î Sn is such that for some i, the (i,s (i))-th entry of A lies in the (p,q)-th block with q > p, then for some j Î Sk with k £ p, s -1(j) Î Sr for an r > p, so that A being block upper triangular the contribution of the permutation s to |A| is zero. This is because if {j : s (j) Î È t£ p St} Ì È t£ p St, then i Î Sp and s (i) Î Sq is contradicted. Hence the only surviving terms in |A| correspond to those s Î Sn which may be written as a product s = s 1s 2…s m, where s p(i) = i if i Ï Sp, i.e., s p permutes withing Sp only, 1 £ p £ m. Using sgn s = sgn s 1 sgn s 2 ... sgn s m, we thus have
![]() .
.
PROBLEMS
1
. What is the determinant of a 1´ 1 matrix?2. If A and B are 2
´ 2 matrices, verify that |AB|= |A||B|.3. If A is 2
´ 3 and B is 3´ 2, prove that |BA| = 0. Construct two pairs of A and B of sizes 2´ 3 and 3´ 2, respectively, such that in one case |AB| = 1 and in the other |AB| = 0.4. Use the definition of the determinant to derive the formulae
(i) ![]() ,
,
(ii) 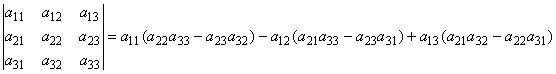 )
)
(iii) If A = (aij ) is n
´ n and is triangular (i.e., either upper, or lower triangular), then det A = a11 a22 a33…ann.
Properties of the Determinant Function
Let A be a square matrix with entries from
F . We describe below some properties of the determinant function, mainly related with certain row operations on A:(1) If B is obtained from A by multiplying some row of it by a scalar c, then det (B) = c det (A).
(2) If B is obtained by interchanging some two rows of A, then det (B) = - det (A).
(3) If B is obtained by adding c-times a row of A to a different row, the det (B) = det (A).
(4) The determinant of the identity matrix I is 1.
(5) If a row of A is zero, det (A) = 0.
(6) If two rows of A are identical, det (A) = 0.
(7) |A| = |A
¢ |.Of these properties: (1) follows from the definition, since in each product
P 1£ i£ n ais (i) precisely one element from each row participates, and it does so linearly. For (2), if i-th and (i+1)-th rows are interchanged, the respective permutations s and s ¢ , say, look like![]() ,
,
![]() .
.
where the omitted entries in the two permutations are the same. For these two permutations the inversions Nj for j < i and for j > i+1 are the same, while Ni + Ni+1 for the two differ by one. Hence sgn (s ¢ ) = - sgn s and (2) follows when two consecutive rows are interchanged. Since, however, an interchange of any two rows, i-th and j-th, say, can be effected by 2|i-j| - 1, an odd number of consecutive row interchanges, the result follows in general. Next we prove (6): In view of (2), via row interchanges, w.l.g. (without loss of generality) let these rows be the 1-st and the 2-nd ones. Then
![]() .
.
The correspondence s « s ¢ , between permutations, where
![]() ,
,
![]() ,
,
may be used to dichotomize Sn into two subsets Sn1 and Sn2 . Note that sgn s ¢ = -sgn s . Hence
![]() .
.
Since, a1s (1) = a2s (1) and a2s (2) = a1s (2), the first two rows being the same, the right hand side is now easily seen as equal to
![]() ,
,
completing the proof of (6).
Property (3) follows from the definition and (1) and (2), for the determinant can be broken as the sum of two determinants: one the original one and the other in which one row is a multiple of another. Taking this multiple out makes two rows same and so this determinant must be zero by (6).
For (5), the zero row could be multiplied by zero without changing the determinant, which by (1) is zero. It also follows since in the product P ais (i) there is one element from each row and so each summand is zero.
To prove (7), let s -1 denote the inverse of the permutation of s :
![]() .
.
By permuting the columns in s -1, we can bring the above to the standard form
![]() ,
,
and we note that this permutation can be brought about by a sequence of interchange of two consecutive columns at a time. Since the number of inversions in the sequence {1, 2, …, n} is zero, the number of inversions in s -1 equals the sum of number of inversions in {s -1(1), s -1(2), … , s -1(n } and in {1, 2, …, n}. But an interchange of two consecutive columns
![]()
affects the number of inversions by
± 1 in both rows and so the sum is affected by an even number only. Thus the number of inversions in s -1 equals the number inversions in s modulo 2, and hence sgn (s ) = sgn (s -1). Using this we have![]() .
.
Finally, (4) is straightforward since in this case the only permutation that contributes a non-zero term is the identity permutation, whose sign is 1 and since each diagonal term is 1. This completes the proof of (1)-(6).
Remark 1. If the field is not of characteristic two, a simpler proof of (6) is as follows: interchanging the identical rows changes the sign of the determinant while the matrix remains the same. Hence the determinant must be its own negative. Thus twice the determinant is zero, which implies that the determinant must be zero.
Remark 2. Another proof of (6) would be via the field F[l ] of fractions in an indeterminate l by putting l = 0 in |(A-l I)(B-l I)| = |A-l I||B-l I|, as here the matrices A-l I and B-l I are not singular with respect of F[l ].
Properties (1)-(4) characterize the determinant function. This becomes clear once we realize, as the reader may easily verify, that using these and the row reduced echelon form we can indeed evaluate a determinant: Let E denote the row reduced echelon form of an n´ n matrix A. If E has a zero row det A = 0. If E has no zero row, E = I in which case, if in obtaining E from A by a succession of elementary row operations one has made a total of p interchanges of rows and a total of q divisions of rows by the pivotal non-zero scalars c1, c2, …, cq, while obtaining the leading unities, det A = (-1)p c1 c2 … cq.
Note that the operation of subtracting a multiple of a row from another does not affect the determinant.
The above properties remain valid with the word 'row' replaced by the word 'column' everywhere. In particular, a similar computation of the determinant of a matrix can be done while reducing the matrix to its column reduced echelon form by using a succession of elementary column operations. One could also mix the row and column operations.
Example. Consider the following reduction of a matrix to an identity matrix by the elementary row and column operations:
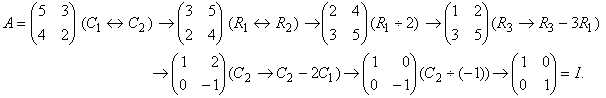 In the above rduction to the identity matrix, there have been a total of p = 2 interchanges of rows and columns and 2 divisions by the pivotal elements c = 2 and c = -1. Hence det A = (-1)2 (2)(-1) = -2.
In the above rduction to the identity matrix, there have been a total of p = 2 interchanges of rows and columns and 2 divisions by the pivotal elements c = 2 and c = -1. Hence det A = (-1)2 (2)(-1) = -2.
Theorem: |AB| = |A||B| = |BA|.
Proof: Row reduce A and column reduce B and keep track of the pivotal dividers and the number of row and column interchanges. If we get a zero row in A or a zero column in B, |A||B| = 0, and the same ER(C)O's render a corresponding row or column of AB zero, so that |AB| = 0 and so |AB| = |A||B|. If this situation does not happen both A and B reduce to I and so the combination reduces AB to I, and the result follows. #
It is easily seen that the above simple proof is not valid if the matrices, instead of being over a field, are over a commutative ring G with identity. This is because of a possible non-existence of the multiplicative inverses of the pivotal elements in G, needed in the row reduction process. An alternate proof of |AB| = |A||B| = |BA|, using block row-column operations, goes as follows:
![]() .
.
Indeed, this proof is perfectly valid for matrices over G.
PROBLEMS
1
. Prove that the determinant of a triangular matrix (i.e., a matrix which is either upper-triangular or a lower triangular) is the product of its diagonal entries.2. Generalize the previous problem to showing that the determinant of a block-triangular matrix is the product of the determinants of its diagonal blocks.
3. For a 2´ 2 matrix A over a field F , show the equation AX = I, where X is a 2´ 2 matrix, has a solution and that it is unique iff det A ¹ 0; and thereby obtain a formula for A-1.
4. Let C be invertible such that C-1AC = U is an n´ n upper triangular matrix. Prove that det A = u11 u11 … unn.
5. Let A be a 2x2 matrix over a field F. Show that there holds det (cI-A) = c2, for each c Î F iff A2 = 0.
6. If a function D : Fn´ n ® F satisfies D(AB) = D(A)D(B) for all A, B, prove that either D(A) = 0 for all A, or D(I) = 1. Give an example of a function D of a latter type which is not the same as the determinant function.
7. If D : ℝ2´ 2 ® ℝ satisfies D(AB) = D(A)D(B) for all A, B and if ![]() , show that
, show that
(a) ![]() ; (b)
; (b) ![]() = -1, D(0) = 0; (c) D(A) = 0, whenever |A| = 0.
= -1, D(0) = 0; (c) D(A) = 0, whenever |A| = 0.
8. Let G denote a commutative ring with identity and G n´ n the set of all n´ n matrices over G . A map D : G n´ n ® G is said to be n-linear if D(A) is linear with respect to each of the n-rows of A while the other n-1 rows are kept fixed. D is called alternating if D(A) = 0 whenever any two rows of A are identical. Show that if D is n-linear and alternating and à is a matrix obtained by interchanging any two rows in A, then D(Ã) = - D(A).
9. If G is a commutative ring with identity such that g + g = 0, g Î G implies g = 0, and if a map D : Gn´ n ® G has the property D(Ã) = - D(A), where à is obtained from A by interchanging any two of its rows, show that D is alternating.
10. If G is a commutative ring with identity 1, D : Gn´ n ® G is (i) n-linear, (ii) alternating and (iii) satisfies D(I) = 1, show that D coincides with the determinant function on Gn´ n.
11. Which of the following D's are 3-linear functions on ℝ3´ 3?
(a) D(A) = a11 a22 a33;
(b) D(A) = (a11 + a22 + a33)(a11 + a22 + a33 );
(c) D(A) = a11 + a22 + a33;
(d) D(A) = a11 a21 a31 + a12 a22 a32 + a13 a23 a33;
(e) D(A) = 0;
(f) D(A) = -1.
12. For an n´ n matrix A over F , verify that D(A) = A(j1,k1)A(j2,k2) ... A(jn,kn). is n-linear if and only if the integers j1, ... , jn are distinct.
13. If G is a commutative ring with identity, verify that the determinant function on the set of 2´ 2 matrices over K is alternating and 2-linear as a function of the rows as well as the columns of A. Does the result generalize to n´ n matrices?
14. If G is a commutative ring with identity and D is an alternating n-linear funciton on Gn´ n, show that (a) D(A) = 0, if one of the rows of A is 0 and (b) D(B) = D(A), if B is obtained from A by adding a scalar multiple of one of its rows to another.
15. For A Î F3´ 3, if
![]() ,
,
prove that if a31 c1 + a32 c2 + a33 c=3 = 0 and (c1, c2, c3)¢ ¹ 0, then rank A = 2 and that (c1, c2, c3)¢ is a basis for the solution space of the system of equations Ax = 0. Think about an appropriate generalization in the n´ n case.
16. Let G be a commutative ring with identity, and let D be an alternating n-linear funciton on Gn´ n. Show that D(A) = (det A)D(I) for all A and deduce that det (AB) = (det A)(det B) for any A, B Î Gn´ n.
17. If F is a field, the set of all matrices of the form f(A), where f is a polynomial over F and A Î F2´ 2 , is a commutative ring G with identity. If A Î F2´ 2 and I Î F2´ 2 is the identity matrix prove that for the matrix
![]() Î G2´ 2,
Î G2´ 2,
det B = f(A) = 0, where f = x2 - (a11 +a22 )x + det A.
18. If A is an n´ n skew-symmetric matrix (i.e., A¢ = -A) over a field F of characteristic not equal to 2 and if n is odd, show that det A = 0.
19. If A is an n´ n real skew-symmetric matrix and n is even, show that det A > 0.
20. If A is a 3´ 3 skew-symmetric matrix over a commutative ring G show that det A = 0.
21. The Vandermonde matrix A defined by aij = xij-1, 1 £ i, j £ n, xi Î F, 1 £ i £ n, has det A = P 1£ j£ i£ n (xi -xj).
22. Use the definition of a determinant to complete the formula det A = a11 a22 a33 + …, for the determinant of a 3´ 3 matrix.
23. Find the subgroup of S5 generated by the two permutations
![]() ,
,
and determine the sign of each permutation in the subgroup.
24. Prove that an n´ n A is invertible over a field iff det A ¹ 0.
25. If A is a 2´ 2 matrix over a field F, show that (a) det (I+A) = 1 + tr A iff det A = 0; (b) det (I+A) = 1 + det A iff tr A = 0.
26. Verify that the determinant of a triangular matrix is the product of its diagonal entries.
27. If A is a 3´ 3 complex matrix and f(x) = det (xI-A), show that f is a monic polynomial of degree 3. If c1, c2, c3 are the roots of f, prove that: (a) c1 + c2 + c3 = tr (A) and (b) c1c2c3 = det A.
28. If A is an n´ n matrix over a field F, and det (xI-A) = (x-l 1)(x-l 2) ... (x-l n), prove that the sum of the products of l i 's taken k at a time equals the sum of all k´ k principal minors of A.
29. Let s Î Sn. If P is an n´ n (permutation) matrix with elements defined by: pij = d s (i)j, 1 £ i, j £ n, show that det P = sgn s.
30. Prove that there exist only three integer valued functions f satisfying f(s t ) = f(s )f(t ), s , t Î Sn: (i) f º 0, (ii) f º 1, and (iii) f(s ) º sgn s , s Î Sn.
31. Show that the set A of alternating n-linear functions on F m´ n, with usual operations, is a vector space and find dim A.
32. If for a s Î Sn, and an n´ n matrix A over a field F with column vectors C1, …,Cn, s (A) denotes the n´ n matrix with the column vectors Cs (1), …, Cs (n), which of the following assertions are true: (a) s (A) is similar to s (I)A; (b) s (AB) = As (B); (c) |s (AB)| = |s (A)||s (B)|; (d) |s (AB)| = |s (A)||B|; (e) s -1(I) = (s (I))-1?
33. For A, B Î Fn´ n if DA(B) = |AB|, show that: (a) DA is an alternating n-linear function; (b) DA(B) = a|B|, where a = DA(I). Is it true that a = |A|?
Cofactor Expansion
The determinant of A after deleting its i-th row and j-th column is called the (i,j)-th minor of A. Let Mij denote the (i,j)-th minor of A. The (i,j)-th cofactor Cij of A is defined by Cij = (-1)i+j Mij. The coefficient of ann in |A| is
![]() .
.
To find the coefficient of aij we interchange i-th row with i+1, i+2, ... , n and the j-th column with j+1, j+2, ... , n, successively . These constitute n-i+n-j negative signs multiplying the determinant without changing the minor. Hence the coefficient of aij is (-1)n-i+n-j Mij = (-1)i+j Mij = Cij. Consequently
|A| = S 1£ i£ n (-1)i+jMijaij = S 1£ j£ n (-1)i+jMijaij = S 1£ i£ n Cijaij = S 1£ j£ n Cijaij.
Combining with the property (6) of determinants, this gives
S
1£ i£ n Cipaiq = d pq|A| = S 1£ j£ n Cpjaqj,where
d pq is the Kronecker delta.We define the classical adjoint or the adjugate of a matrix A as Adj (A) = (Cji) = (Cij)
¢ . Thus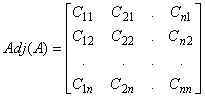 .
.
Hence
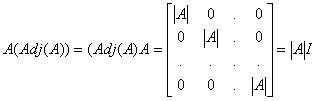 .
.
It follows that if |A| ¹ 0, then
![]() .
.
Cramer's Rule: If A is non-singular and Ax = b, then xj = det ([A|b]j)/det (A), j = 1, 2, …, n, where [A | b]j stands for the matrix obtained from A by replacing its j-th column by the vector b.
The proof of the Cramer's rule follows from xj = (A-1b)j = (|A|-1[Adj (A)]b)j = |A|-1S 1£ i£ n Cijbi =det([A|b]j)/|A|.
Example 1. We find the eigenvalues of the n´ n complex matrix
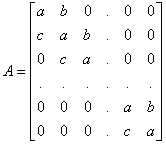 .
.
The eigen-values constitute the numbers l that make det (l I-A) zero. Denoting the determinant of A by Dn, we have: D1 = a, D2 = a2 - bc and the recurrence relation: Dn = aDn-1 - bcDn-2, (n ³ 3), the characteristic equation of which is: x2 - ax + bc = 0, with the roots: x = [a± Ö (a2 - 4bc)]/2, so that for some constants a , b , we have:
Dn = a ([a+Ö (a2 - 4bc)]/2)n + b ([a-Ö (a2 - 4bc)]/2)n , n ³ 1.
Taking n = 1 and 2, respectively, we get
a = a ([a+Ö (a2-4bc)]/2)+b ([a-Ö (a2-4bc)]/2),
a2-bc = a ([a+Ö (a2-4bc)]/2)2+b ([a-Ö (a2-4bc)]/2)2
= a ([2a2-4bc+2aÖ (a2-4bc)]/4)+b ([2a2-4bc-2aÖ (a2-4bc)]/4)
= a(a ([a+Ö (a2-4bc)]/2) + b ([a-Ö (a2-4bc)]/2)) - (a +b )bc
= a2 -bc(a +b ).
Note that if any of b or c is 0, the only eigenvalue of A is a algebraically repeated n times. Hence, without loss of generality we can assume that bc ¹ 0. Then, a +b = 1, a -b = a/Ö (a2-4bc), so that a = (1+a/Ö (a2-4bc))/2, and b = (1-a/Ö (a2-4bc))/2, and, consequently, Dn = (Ö (a2-4bc))-1[((a+Ö (a2-4bc))/2)n+1-((a-Ö (a2-4bc))/2)n+1]. If a2 ¹ 4bc and Dn = 0, then a+Ö (a2-4bc) = (a-Ö (a -4bc))w n+1, where w n+1 ¹ 1 is an (n+1)-th root of unity. Then (a2-4bc)(1+w n+1)2 = a2(1-w n+1), i.e., a = [bc(1+w n+1)2/w n+1]1/2 = [bc(w n+1-1+2+w n+1)]1/2 = 2Ö (bc) cos (p k/(n+1)), (1 £ k £ n).
It follows that the n-eigenvalues of A are given by l k = a-2Ö (bc) cos(p k/(n+1)), (1 £ k £ n), and are distinct. By a continuity argument the eigenvalues continue to be given by the above expression in all exceptional cases too.
Example 2. We evaluate the determinant of the matrix
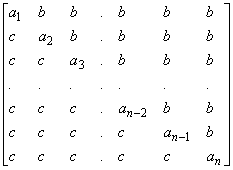
Let U denote the n
´ n matrix with all entries 1. Subtracting the first row of A(x) = A-xU from the rest, it follows that det(A-xU) is a linear function of x. If f(x) = P 1£ i£ n (ai-x), we then have det(A(b)) = f(b) = a b+b , det(A(c)) = f(c) = a c+b , say. It follows that det A = det A(0) = b = (cf(b)-bf(c))/(c-b). If b = c, passing to the limit as c ® b, we have det A = f(b)-bf¢ (b).
PROBLEMS
1
. Prove that a lower (upper) triangular matrix has an inverse iff none of its diagonal entries is zero and, moreover, the inverse of such a matrix is also lower (upper) triangular.2. For a 3´ 3 matrix A, expand the three functions C1, C2, C3:
![]() ,
,
![]() ,
,
![]() ,
,
to verify that they are identical and equal |A|.
3. If A is an n´ n matrix over a commutative ring G with identity, verify that
(a) (adj A)A = A(adj A) = (det A)I;
(b) det (adj A) = [det (A)]n-1;
(c) adj (A¢ ) = (adj A)¢ .
4. If P and Q are invertible and distinct, PA is row reduced echelon and AQ is column reduced echelon, show that A is singular.
5. If A, P and Q are non-singular, PA is row reduced echelon and AQ is column reduced echelon, prove that P = Q = A-1.
6. Find invertible P, Q, a row reduced echelon matrix R and a column reduced echelon matrix C such that R = PA and C = AQ for the following matrices A:
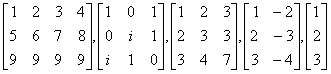 .
.
7. For each of the following A Î C 3´ 3, find all x Î C 3 and c Î C such that there holds Ax = cx:
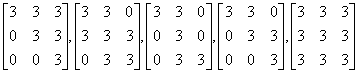 .
.
8. Find inverses of those of the following matrices that are invertible
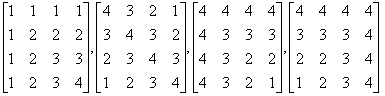 .
.
9. If A, B Î Fn´ n, and AB is invertible, prove that A and B are also invertible.
10. If A is an n´ n matrix, prove that: (a) if A is non-singular and AB = 0 then B = 0, (b) if A is singular there exists an n´ n matrix B such that AB = 0 but B ¹ 0 and (c) if A ¹ 0 is singular and AB = 0 then B is singular.
11. Use elementary row operations to show that ![]() is invertible iff ad ¹ bc.
is invertible iff ad ¹ bc.
12. If A is m´ n and B is n´ m and AB is invertible, prove that r(A) = r(B) = m. Is the connverse true?
13. If A is m´ n and B is n´ m and n < m, use (a) elementary row operations and (b) elementary column operations, to show that AB is not invertible.
14. Find the total number of m´ n matrices R which are both 'row-reduced echelon' and 'column-reduced echelon.' Also prove that for any m´ n A there exist invertible m´ m P and n´ n Q such that for a matrix R of the above type A = PRQ. Are such P and Q unique in general? When would they be unique?
15. Prove that for any non-negative integer p, the m´ m matrix
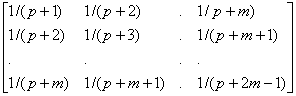
is: (a) non-singular, (b) positive definite, and that (c) its inverse has only integral entries with alternating signs.
16. A complex n
´ n matrix A is called strictly diagonally dominant with respect to rows if |aii| > S |j-i|>1 |aij|, 1 £ i £ n. The matrix is called strictly diagonally dominant with respect to columns if |ajj| > S |i-j|>1 |aij|, 1 £ j £ n. Prove that a matrix which is strictly diagonally dominant with respect to either rows or columns is non-singular.17. If A is hermitian, has positive diagonal elements and is strictly diagonally dominant with respect to rows, show that A must be positive definite.
18. Is it true that the inverse of a Hessenberg matrix is also Hessenberg.
19. If A, B are invertible, prove that AB is invertible and that (AB)-1 = B-1A-1. Also show that (AB)-1 = A-1B-1 iff A and B are invertible and AB = BA.
20. Use the classical adjoint formula to compute the inverses of each of the following 3
´ 3 real matrices: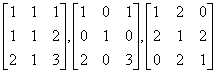 .
.
21. Use Cramer's rule to solve the following real systems:
(a) 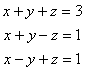 , (b)
, (b) 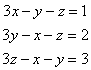 , (c)
, (c) 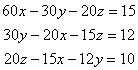 .
.
22. Let A be an n´ n skew-symmetric matrix over a field F. If F is not of characteristic 2 and if n is odd, show that |A| = 0.
23. Let A be an n´ n real skew-symmetric matrix. If c is a real number and |A+cI| < 0, prove that c < 0 and n is odd.
24. If A is an n´ n matrix and AAt = I, show that |A| = ± 1.
25. If A is an n´ n matrix and A2 = I, show that |A| = ± 1.
26. If A is a complex n´ n matrix and AA* = I, show that |det (A)| = 1.
27. If A is a block upper triangular matrix over a commutative ring G with identity, |A| = |A1||A2 |…|Ak|, where the matrices A1, A2, …, Ak denote the square diagonal blocks of A.
28. If A is an n´ n matrix over a field F, show that there exist at most n distinct scalars c Î F such that cI-A is not invertible.
29. If F is a non-algebraically closed field there exists a matrix A over F such that |cI-A| = 0 for no c Î F.
30. If A, B Î Fn´ n and if A is invertible prove that there are at most n scalars c Î F such that |cA + B| = 0.
31. If A, B, C, D Î Fn´ n, and if A commutes with C, show that ![]() = det (AD-BC).
= det (AD-BC).
Rank of a Matrix
Note that the span of an ordered set of vectors remains unchanged if elementary operations (corresponding to eros) viz., interchanging the order or position of two vectors, multiplying a vector by a non-zero scalar, and adding a scalar multiple of a vector to another, are performed on the set. The dimension of the span of a set of vectors is the maximal number of linearly independent vectors in the set. Hence, the elementary operations do not change the maximal number of linearly independent vectors in the set. The row rank (rr(A)) of a matrix A is the maximal number of linearly independent rows of the matrix. Similarly, the column rank cr(A) is the maximal number of linearly independent columns of A. It follows that if E is the row-reduced echelon form of A and F is the column-reduced echelon form of A, then rr(A) = rr(E) and cr(A) = cr(F). The row (column) space of a matrix being the span of its row (column) vectors has dimension rr(A) (cr(A)).
The determinantal rank (dr(A)) of the matrix A is the largest p such that A has a p
´ p submatrix with non-zero determinant. It is an interesting fact that all the above three notions of rank of any m´ n matrix coincide:Theorem. rr(A) = cr(A) = dr(A).
Proof. The rows of the highest order submatrix of non-zero determinant must be linearly independent (else its determinant equals 0). Then all the more so are the same rows of the full matrix. Hence rr(A)
³ dr(A).Next, take a maximal collection of linearly independent rows and make a submatrix out of them. Row reduce it to its echelon form. Then each row of the echelon form must have a leading unity (as the rows are linearly independent). The submatrix of A consisting of these rows and the columns that contain leading unities of the echelon form is of a non-zero determinant. It follows that dr(A)
³ rr(A). Hence rr(A) = dr(A). Since dr(A) is symmetric with respect to rows and columns [det (B) = det (B¢ )] we have rr(A) = dr(A) = cr(A). #In view of the above theorem we define rank, r(A), of the matrix to be any of the same rr(A), cr(A) and dr(A).
Theorem. r(AB)
£ min{r(A), r(B)}.Proof. Rows of AB are linear combinations of rows of B and columns of AB are linear combinations of columns of A. Hence rr(AB)
£ rr(B) and cr(AB) £ cr(A), from which the result follows. #Theorem. r(A+B)
£ r(A) + r(B).Proof. Row space of A + B is contained in the span of the rows of A and B pooled together, from which the result is clear. #
Theorem. If A is a complex matrix, r(A) = r(A
* A) = r(AA* ).Proof. Ax = 0 implies A
* Ax = 0. Conversely if A* Ax = 0 it follows that (Ax)* Ax = 0, which implies Ax = 0. Thus Ax = 0 iff A* Ax = 0. Let the j-th column of B be denoted by Bj. Then we have S xjAj = 0 iff S xj(A* A)j = 0. Thus a collection of columns A is dependent iff the collection of the same columns of A* A is dependent. Hence cr(A) = cr(A* A). Since r(A) = r(A¢ ) = r(A')- = r(A* ), it follows that cr(A) = cr(AA* ). The result is immediate from this. #It follows along the lines of the proof of the above result that the rank of any finite product of A and A
* , in which they consecutively occur (e.g., A* AA* AA* A, AA* AA* A, A* AA* AA* ) equals the rank of A.
Problems
1
. r(AB) + r(BC) £ r(B) + r(ABC).2. Let A = B + iC where B = (A+Ā)/2 and C = -i(A-Ā)/2. If A is positive (negative) semi-definite (it includes p.d. or indefinite etc.) then r(B)
³ max {r(A), r(C)}.3. If ![]() is p.s.d.,
is p.s.d.,
4. If A is m
´ n and B is p´ n, then Bx = 0 whenever Ax = 0, iff there exists a p´ m C such that B = CA.5. Let
a 1, a 2, …,a m Î Fn . Show that: (a) a 1, a 2, …,a m are l.i. (linearly independent) iff the column-reduced echelon form of [a 1 | a 2 | … | a m] has no zero columns. (b) The dimension of the subspace spanned by a 1, a 2, …, a m equals the number of non-zero columns in the column-reduced echelon form of [a 1 | a 2 | … | a m], which actually form a basis of the subspace. (c) b Î <a 1, a 2, …,a m> (<S> denoting span of S) iff [a 1 | a 2 | … | a m]x = b is consistent. (d) If E denotes the column-reduced echelon form of A and if the leading entries in E occur in the rows i(1) < … < i(r), then b Î <a 1, a 2, …,a m> iff b = S 1£ k£ r b i(k) Ek , where Ek stands for k-th column of E = (eij).6. Linear two-point boundary conditions for a system of n-first order differential equations: dy/dx = f(x,y), a < x < b, are of the type Ay(a) + By(b) = c
Î R n. Show that these boundary conditions are linearly independent iff r(A|B) = n. Show also that r(A|B) = n iff there exist n´ n matrices E and F such that AE + BF is non-singular.7. Let Eij denote the n
´ n matrix whose (i,j)-th entry is 1, while the rest of the entries are zero. Find the ranks of the matrices Eij + Ekl , Eij - Ekl and EijEkl.8. Prove that if for some i < j, r(Ai) = r(Aj), then for all k, l > i, r(Ak) = r(Al).
9. Prove that if A is n
´ n, then r(An) = r(An+1).10. If A is an n
´ n matrix, there exists another n´ n matrix B of rank n-r(A) such that AB = 0.11. A matix is of rank 1 iff it can be written as xy , where x and y are non-zero column vectors.
12. If A is an m
´ n matrix satisfying apq + ars = aps + arq for all possible p, q, r, s, prove that there exist bi 's and cj 's such that aij = bi + cj , for all i and j. Find the rank of such a matrix.13. Find the rank of the n
´ n matrix
for different a and b
Î F .
The System of Linear Equations: Ax = b
If A1, A2, ... , An denote the columns of a matrix A, the system of equations Ax = b can be written as x1A1 + x2A2 + ... + xnAn = b.Thus Ax = b has a solution iff r(A) = r(A|b), i.e., the rank of A, the matrix of the system, equals the rank of the augmented matrix [A|b] of the system.
Since the eros are reversible, their application on the augmented matrix [A|b] of a system Ax = b results in an augmented matrix [E|f], with E in a row-reduced echelon form, of an equivalent system Ex = f of linear equations in the sense that x is a solution of one system iff it is a solution of the other. This reduction of the A part (the matrix part) of [A|b] to its row-reduced echelon form, while performing the elementary row operations on the whole of [A|b] leads to the following:
Theorem. Let A
Î Fm´ n, b Î Fm and [E | f] be row equivalent to [A | b] with E in the row-reduced echelon form. The matrix [E | f] can be obtained by performing elementary row operations on [A | b]. Then: (a) Ax = b has a solution (i.e., it is consistent) iff whenever a row in E is zero, the corresponding entry in f is also zero. (b) If Ax = b is consistent, its general solution can be expressed in a parametric form with the minimum number of parameters equaling the number of free columns in the row-reduced echelon form E of A, which is also equal to the nullity of A: xj(i) = fi - S jÎ S eijxj, 1 £ i £ r(A), where S denotes the set of free column nrs., j(i) is the column nr. of the leading unity in the i-th row, and eij is the (i, j)-th element in E. (c) If m = n, the following statements are equivalent: (i) Ax = b has a solution for each b; (ii) Ax = 0 has only a trivial (x = 0) solution; (iii) A is non-singular; (iv) |A| ¹ 0; (v) Ax = b, for some b, has a unique solution.
PROBLEMS
1
. The solutions of Ax = 0 form a subspace (null space N (A) of A) of Fn, where A Î Fm´ n. The dimension of N (A) equals n-r(A).2. A general solution of the inhomogeneous system Ax = b is a particular solution of it plus a general solution of the homogeneous system Ax = 0.
3. If A is m
´ n and r(A) = m, then Ax = b is consistent for each b.4. If A is m
´ n, then r(A) = n iff Ax = 0 has only the trivial solution.5. If the rows, as well as the columns of a matrix are linearly independent then the matrix is a square matrix.
6. Let A, B
Î C m´ n and u Î C n. Show that the two systems of linear equations A* x + B* y = u, and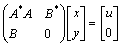 ,
,
are either both consitent or both inconsistent.
7. Prove that two consistent systems of linear equations have the same solutions iff they are equivalent. Deduce that if two homogeneous systems of linear equations have the same solutions then they are equivalent.
8. Let m > n be positive integers. Give examples of n´ n, m´ n and n´ m systems Ax = b of linear equations which have: (a) no solution, (b) a unique solution, (c) infinitely many solutions and (d) more than one but only finitely many solutions.
9. Suppose R and S are row-reduced echelon matrices and that the systems Rx = r and Sx = s have exactly the same solutions. Prove that R = S and r = s.
10. A non-singular n´ n matrix A has a representation A = LU, where L is a lower triangular and U upper triangular iff its principal submatrices Ak defined as A = (aij)1£ i,j£ k , 1 £ k £ n, are invertible.
11. An n´ n complex matrix A can be factorized as A = LL* , where L is a non-singular lower triangular matrix iff A is positive definite (i.e., x* Ax > 0 for all 0 ¹ x Î C n).
12. Consider the system Ax = b, where aij, bi Î R , 1 £ i £ m, 1 £ j £ i. Prove that x Î R n minimizes the expression (b-Ax)¢ ( b-Ax) = S 1£ i£ m (bi - S 1£ j£ n aijxj)2 iff x is a solution of the system of equations: A¢ Ax = A¢ b.
13. Let aij, bi Î C , 1 £ i £ m, 1 £ j £ i. Prove that x Î C n minimizes (b-Ax)*( b-Ax) = S 1£ i£ m |bi - S 1£ j£ n aijxj|2 iff x is a solution of the system of equations: A*Ax = A*b.
14. Let aij, bi Î R , 1 £ i £ m, 1 £ j £ i. Prove that the system of equations: A¢ Ax = A¢ b is consistent.
15. Let aij, bi Î C , 1 £ i £ m, 1 £ j £ i. Prove that the system of equations: A*Ax = A*b is consistent.
16. Let A be an n´ n matrix over a field and E be the row reduced echelon form of A. Prove that |A| ¹ 0 iff E = I.
17. Let A be n´ n and let a succession of elementary row operations on [A | b | I], which is A augmented with b and the identity matrix, result in [I | x | B]. Prove that A is non-singular, x is the solution of Ax = b, and B = A-1.
18. Let A be n´ n and a succession of elementary row and column operations on A result in I. Prove that the same operations turn I into A-1. If the number of row and column interchanges in these operations is m and if c1, c2, … , ck denote the scalars by which the rows/columns were divided, prove that |A| = (-1)m P 1£ j£ k cj.
19. Prove that performing an elementary row or column operation on a matrix does not change its rank.
20. Verify that performing a succession of elementary row (column) operations on an m´ n matrix is equivalent to pre (post) multiplication of the matrix by the matrix that is obtained by performing the same operations on the identity matrix Im (In).