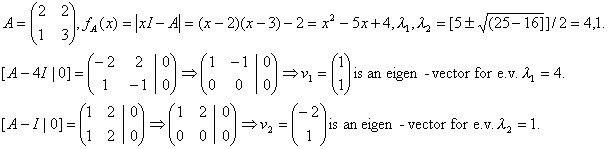
Eigenvalues and Eigenvectors

Let A be an n´ n matrix over a field F . We recall that a scalar l Î F is said to be an eigenvalue (characteristic value, or a latent root) of A, if there exists a nonzero vector x such that Ax = l x, and that such an x is called an eigen-vector (characteristic vector, or a latent vector) of A corresponding to the eigenvalue l and that the pair (l , x) is called an eigen-pair of A. If l is an eigenvalue of A, the equation: (l I-A)x = 0, has a non-trivial (non-zero) solution and conversely. Thus, this being a homogeneous equation, it follows that l is an eigenvalue of A iff |l I-A| = 0. The expression

is a monic (the coefficient of the highest power of x in it is 1) polynomial in x of degree n. It is known as the characteristic polynomial of A. Thus l is an eigen value of A iff l is a zero (or root) of the characteristic polynomial f_A(x) in F. The equation

is called the characteristic equation of A. Note that the coefficients of the characteristic polynomial are elements of field F under consideration. If F is an algebraically closed field (for instance, ℂ) we know that a polynomial of precise degree n has precisely n roots counted after multiplicities. Thus, for instance, a complex n´ n matrix has n eigen values counted after multiplicities.

Note that l = 0 is an eigenvalue of A iff |A| = 0, i.e., A is a singular matrix. If an eigenvalue l of A is known, the corresponding eigenvector(s) may be obtained by elementary row operations (ero's) performed on the matrix part of the augmented matrix [A-l I|0].

Example: Computation of eigen-values and eigen-vectors of a 2´ 2 complex matrix: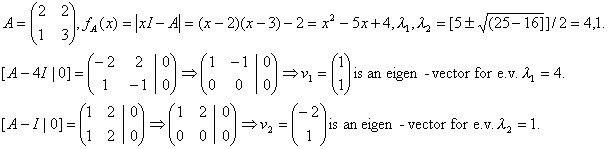

The algebraic multiplicity of an eigenvalue l of A is the highest k such that (x-l )^k is a factor of f_A(x). The geometric multiplicity of an eigenvalue l of a matrix A is the maximum number of linearly independent eigen vectors x of A associated with the eigenvalue l , which is the same as the dimension of the eigenspace of A associated with the eigenvalue l consisting of all x such that Ax = l x. This eigenspace is the same as N(A-l I).

A collection of eigenvalues of A in which an eigenvalue is repeated according to is algebraic multiplicity is called the spectrum of A, and is denoted by s (A). Clearly, if s (A) = {l , l , ... , l }, f_A(x) = P (x-l ). Thus, e.g., for an identity matrix: s (I) = {1, 1, ... , 1}, for a null or zero matrix s (0) = {0, 0, …, 0},

s ( ) = {1, 3}, s ( ) = {1, 1}, s ( ) = {2+Ö 5, 2-Ö 5}, and, s ( ) = {0, 4}.

A matrix B is said to be similar to a matrix A (written: B ~ A) if there exists a non-singular matrix C such that C^-1AC = B. This relation is interpreted as follows : if instead of the standard basis of the unit vectors e₁ = (1, 0, 0, ... , 0)¢ , e₂ = (0, 1, 0, ... , 0)¢ , ... , e_n = (0, 0, 0, ... , 1)¢ , we choose the basis of Fⁿ to consist of the column vectors of the matrix C, then the matix of the transformation A turns out to be B. It follows that A ~ A (reflexivity); B ~ A implies A ~ B (symmetry); and A ~ B and B ~ C implies A ~ C (transitivity). The similarity relation therefore is an equivalence relation. Consequently the set of all n´ n matrices over a field F can be decomposed into (written as a union of) mutually exhaustive equivalence classes of all matrices which are similar to each other.

Companion Matrices and Characteristic Polynomial

,

,

,

.

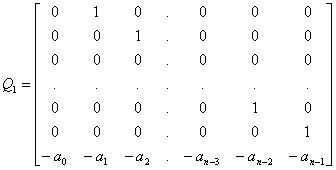Method of Danilevsky for Characteristic Polynomial

A matrix transformation of type: A Î F ⁿ´ n ® C^-1AC, (C non-singular) is called a similarity transform. The matrix C^-1AC is said to be similar to A. The characteristic polynomial remains invariant under a similarity transform, i.e., similar matrices have the same characteristic polynomial:

.

.

(1) X ¬ A (i.e., copy A in X);

(2) k ¬ 2;

(3) If x_{j k-1} = 0, for all j ³ k, X has the reducible form ,

(4) If x_{j k-1} ¹ 0, for some j ³ k, interchange the j-th row with the k-th row and the j-th column with the k-th column (a similarity transform) after which x_{k k-1} ¹ 0. Next:

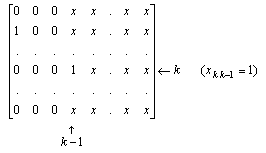
(ii) for all i ¹ k, from the i-th row subtract x_i1 times the k-th row and to the k-th column add x_i1 times the i-th column (it constitutes a similarity transform). X looks like:

(5) If k < n, k ¬ k+1. Go to step (3).

PROBLEMS

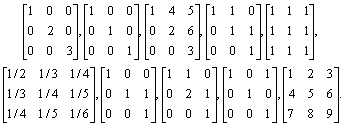
2. Construct 2´ 2 and 33 matrices that, if possible, have (a) no eigenvalues, (b) all distinct eigenvalues, (c) all coincident eigenvalues, (d) some but not all distinct eigenvalues, (e) a full set of eigenvectors, (f) only one linearly independent eigenvector, and (g) every non-zero vector as an eigenvector.

3. Characterize 2´ 2 matrices to each of which there corresponds another matrix differing from it in only one element but having the same spectrum.

4. If v₁, v₂, …, v_n are the eigenvectors associated with the respective eigenvalues l ₁, l ₂, … , l _n of an n´ n matrix A and none of the l 's is zero and b = S ₁£ k£ n c_kv_k, show that the solution of the system Ax = b is given by

x = S ₁£ k£ n (c_k/l _k)v_k.

5. When is it possible to write every vector in Fⁿ as a linear combination of eigenvectors of a matrix A? Give an example of a matrix A for which it is possible. Give another example for which it is not.

6. If the geometric multiplicity of an eigenvalue l of an n´ n matrix A is n-k+1, prove that every k´ k principal submatrix (i.e., a submatrix whose diagonal lies along the diagonal of the matrix) of A has l as one of its eigenvalues.

7. Let E be n´ k, W n´ (n-k) and A an n´ n matrix over a field F. If the n´ n partitioned matrix C = (E!W) is non-singular and the columns of E are eigen-vectors of A show that

where D is a diagonal matrix, 0 is the (n-k)´ k zero matrix and X and Y are matrix blocks satisfying

9. Verify that similarity is an equivalence relation, i.e., it is reflexive (A ~ A), symmetric (B ~ A Þ A ~ B) and transitive (A ~ B, B ~ C Þ A ~ C).

Matrices with a Full-Set of Eigen-Vectors

An n´ n matrix is said to have a full set of eigenvectors if there exist n linearly independent vectors v₁, v₂, ... , v_n, which at the same time are also eigenvectors of A. In other words an n´ n matrix A has a full set of eigenvectors iff there exists a basis of Fⁿ, consisting entirely of the eigenvectors of A. If the associated eigenvalues are l ₁, l ₂, … , l _n and C denotes the matrix whose j-th column vector coincides with the eigenvector v_j, we have AC = C diag (l ₁, l ₂, … , l _n). Further, since the vectors v_j 's are linearly independent, the matrix C is non-singular and we may write the above equation as C^-1AC = D, where D = diag (l ₁, l ₂, … , l _n). Conversely if C^-1AC = D, the n column vectors of the matrix C constitute n linearly independent eigenvectors of the matrix A corresponding to the eigenvalues l ₁, l ₂, … , l _n that are the diagonal entries of the diagonal matrix D. Thus we have proved the following:

PROBLEMS

2. Find a matrix A with distinct eigenvalues c₁, c₂, ... , c_k, for which (c₁I-A)(c₂I-A) ... (c_kI-A) ¹ 0.

5. Relate f_A(x) and f_B(x) if B = A = (A¢ )* , a complex matrix.

6. If A is a complex matrix relate f_A(x) and f_B(x) if B = A* .

7. If P(x) is polynomial function and s (A) = {l ₁, l ₂, ..., l _n}, when does there hold s (P(A)) = {P(l ₁), P(l ₂), ..., P(l _n)}?

11. Which of the following matrices is diagonalizable over R:

.

12. There are 24 distinct 2´ 2 matrices with distinct entries taking the values 1, 2, 3 and 4, only. Show that: (a) all of these are diagonalizable over C ; (b) all of these are diagonalizable over R ; and (c) only those of these are diagonalizable over Q that have 5 as an eigenvalue.

13. Can you show that given any n´ n complex (real) matrix A and a positive number e , there exists another complex (real) matrix A having a full set of eigenvectors such that no entry of A differs from that of the corresponding entry of A by more than e ?

14. If an invertible complex matrix A equals its inverse A^-1, prove that it has a full set of eigenvectors. Is the result true if F ¹ C .

The Cayley-Hamilton Theorem

If A is an n´ n matrix over a field F and k = n², the matrices I, A, A², ... , A^k (being n²+1 in number) are linearly dependent in F^{n´ n} . Hence there exist scalars c₀, c₁, c₂, ... , c_k, not all zero (termed non-trivial scalars) such that c₀I + c₁A + c₂A² + ... + c_kA^k = 0. Thus with P(x) = c₀ + c₁x + c₂x² + ... + c_kx^k, we have P(A) = 0, i.e., any n´ n matrix A satisfies a non-trivial polynomial equation of degree £ n². The Cayley-Hamilton theorem asserts that the familiar characteristic polynomial f_A(x) itself kills (annihilates) A:

Proof: Consider the linear polynomial matrix A(x) = xI-A (its entries are linear polynomials in x). Let C_ij(x) denote its (i, j)-th cofactor, which for each pair (i, j) is a matrix polynomial of degree n-1, at most. Using cofactor expansion identities we have d _ki f_A(x) = S ₁£ j£ n C_kj(x)(d _ijx-a_ij), where the elements are from the i-th row whereas the cofactors are corresponding to the k-th row. Evaluating the two polynomial sides at the matrix A, we have d _ki f_A(A) = S ₁£ j£ n C_kj(A)(d _ijA-a_ijI). With e_j 's as the standard unit vectors, we therefore have

f_A (A)e_k = S ₁£ i£ n d _ki f_A(A)e_i = S ₁£ i£ n S ₁£ j£ n C_kj(A)(d _ijA-a_ijI)e_i

= S ₁£ j£ n C_kj(A) S ₁£ i£ n (d _ijA-a_ijI)e_i = S ₁£ j£ n C_kj(A)(A^j -A^j) = 0.

Hence, for any vector x, f_A(A)x = f_A(A) S ₁£ k£ n x_ke_k = S ₁£ k£ n x_kf_A(A)e_k = 0, and consequently f (A) = 0. #

Another simple proof: of the Cayley-Hamilton theorem is as follows: Let B(x) denote the classical adjoint (transpose of the matrix of cofactors) of A(x) = xI-A. If A is n´ n, the entries in B(x) are polynomials in x of a degree not exceeding n-1. Hence we can write

Corollary. Any polynomial in an n´ n matrix A can be written as a polynomial in A of degree n-1 at most.

Proof: If P is a polynomial, write P = f_AQ + R, where R, the residual (remainder) polynomial is of degree < deg f_A = n. Hence P(A) = R(A) and deg R £ n-1. #

The collection of all polynomials P such that P(A) = 0, is non-empty. Hence, as the degree of a non-zero polynomial is a non-negative integer valued funciton, it follows that there exists a monic polynomial p_A(x) of least degree such that p_A(A) = 0. The polynomial p_A(x) is known as the minimal polynomial of A.The minimal polynomial p_A of a matrix A is unique and divides every polynomial P such that P(A) = 0. For, writing P = p Q + R, and evaluating both sides at x = A we get R(A) = 0, but if R ¹ 0, dividing it by its coefficient of highest degree, we have a monic polynomial of a smaller degree than p , a contradiction. In particular, the minimal polynomial divides the characteristic polynomial. Indeed, p_A(x) | f_A(x) is a rephrasing of the Cayley-Hamilton theorem.

PROBLEMS

3. |A| = l ₁ l ₂ … l _n and tr (A) = l ₁ + l ₂ + … + l _n, where l _i 's are eigenvalues of A counted after multiplicities.

5. If l is an eigenvalue of A, P(l ) is an eigenvalue of P(A). Conversely, if m is an eigenvalue of P(A), m = P(l ) for some eigenvalue l of A.

7. If 1 is not an eigenvalue of n´ n matrices A and B, (A+B)x = x iff (I-B)^-1A(I-A)^-1Bx =x. [K.C. Deomurari]

8. If A is an n´ n matrix with distinct eigenvalues c₁, c₂, … , c_k, show that [(c₁I-A)(c₂I-A) ... (c_kI-A)]^n-1 = 0.

Triangulization and Unitary Diagonalization of a Matrix

The interest in the existence and construction of possible similar matrices of a particular type is due to several problems for similar matrices being related: e.g., if A ~ B = C^-1AC, Bx = l x Þ ACx = l Cx; By = C^-1b Þ A(Cy) = b. Thus, if B has a relatively simpler structure, it may enable an easier solution of problems involving A. The case when B could be managed to be a triangular matrix is discussed below.

Theorem. If A is a square n´ n matrix over a field F, there exists a non-singular matrix C such that C^-1AC = T, a triangular (upper) matrix iff the characteristic polynomial f_A(x) = det(xI-A) of A is a product of linear factors.

Proof: Let l be any of the eigenvalues of A and let x be a corresponding eigen-vector. Choose {x, x², x³, … , xⁿ} to be an ordered basis of F ⁿ of which the first member is the vector x. Arrange these basis members as columns of a matrix S = (x | X), where X is an n´ (n-1) block. Then S is a non-singular matrix and

S^-1AS = S^-1 [l x | AX] = ,

,

.

Since for 1´ 1 matrices the result is trivial, we have proved it for matrices of all sizes. The converse statement is trivial, since if A is triangulable, its characteristic polynomial is the same as that of the similar matrix T, which being upper triangular has its characteristic polynomial as P (x-t_ii), a product of linear factors. #

Schur's Lemma and the Spectral Theorem

Consider the case when the field F is the complex field C. Since C is algebraically closed, any polynomial over C is a product of linear factors. Hence any square matrix A over C is triangulabe by some C. If we apply the Gram-Schmidt orthonormalization process to the columns of C and arrange the resulting orthonormalized vectors as the respective columns of E, then E is of the above type and so it also triangulizes A. But E, in addition is unitary, i.e., E* E = I. Thus we have proved the following:

Schur's Lemma: Given any square complex matrix matrix A, there exists a unitary matrix U such that U* AU = T, a triangular matrix, i.e., any complex matrix can be unitarily triangulized.

As a corollary, we may deduce the following important result known as unitary diagonalization, or, spectral theorem for normal matrices. Recall that a complex matrix A is called normal if A* A = AA* .

Theorem (Spectral). If A is a square complex matrix, there exists a unitary matrix U such that U* AU = D, a diagonal matrix, iff A is normal.

Proof: If A is unitarily diagonalizable, A = UDU* , and so AA* = UDD* U = UD* DU = A* A, i.e., A is normal. Conversely, let A be normal. By Schur's lemma, A = UTU* and so the normalcy implies that UTT* U* = UT* TU* . Then TT* = T* T. Since T is upper triangular, its elements below the main diagonal are zero, i.e., t_ij = 0, if i > j. Equating the first diagonal elements on both sides of the normalcy equation for T we get |t₁₁|² + |t₁₂|² + |t₁₃|² + ... + |t_1n|² = |t₁₁|², so that all strictly upper-triangular terms in the first row are zero. Next equating the second diagonal elements |t₂₂|² + |t₂₃|² + ... + |t_2n|² = |t₂₂|², so that all elements in the strictly upper-triangular part in the second row are zero. Comparing the third elements then gives |t₃₃|² + ... + |t_3n|² = |t₃₃|², so that all strictly upper-triangular terms in the third row are zero, and so on till |t_{n-1 n-1}|² + |t_{n-1 n} |² = |t_{n-1 n-1}|², which says that t_{n-1 n} = 0. Thus we find that t_ij = 0 whenever i ¹ j, i.e., T is a diagonal matrix. This completes the proof of the unitary diagonalization theorem. #

A matrix A which is hermitian (i.e., A* = A) is automatically normal and so it is unitarily diagonalizable. Since the eigenvalues of a hermitian matrix are real, the corresponding diagonal form is real. Since a real symmetric matrix A (i.e., A¢ = A, and A is with real entries) is hermitian, regarding it as a matrix over C we find that its characteristic polynomial is a product of real linear factors. But its characteristic polynomial over R is the same as over C. Hence regarded as a matrix over R its characteristic polynomial is a product of linear factors. Since to a real eigenvalue of a real matrix there always corresponds a real eigen-vector, repeating everything in the above for this special case of a real symmetric A with F as R , we obtain the following:

Spectral Theorem for Real Symmetric Matrices. If A is a real matrix, there exists a real orthogonal matrix U (i.e., a real matrix U such that U¢ U = I) such that U¢ AU = D, a diagonal matrix, iff A is symmetric.

PROBLEMS

1. For an n´ n A, (A+A* )/2 and (A-A* )/2 are respectively known as the hermitian and skew-hermitian parts of A; for a real matrix these respectively become the symmetric and skew-symmetric parts. Prove that A is normal iff its hermitian and skew-hermitian parts commute. Deduce that a hermitian, or a skew-hermitian matrix is normal.

4. Inter-relate the hermitian and skew-hermitian parts of A and iA. [i = Ö (-1)].

10. If l ₁, … , l _n are the eigenvalues of a complex n´ n matrix A, prove that |l ₁|² … + |l _n|² £ S ₁£ i£ n S ₁£ j£ n |a_ij|², and that the equality holds iff A is normal.

The Equation: AX - XB = C

We use the result on triangulization to infer about a unique solvability of the matrix system AX - XB = C of equations, in which A is m´ m, X m´ n, B n´ n and C an m´ n matrix. The size constraints make the equation meaningful. The set of eigenvalues of a matrix A is denoted by s (A) and is called the spectrum of A.

Theorem. A complex system AX - XB = C has a unique solution iff s (A)Ç s (B) = f , the null set.

Proof. If n = 1, the system reduces to (A - b₁₁I)X = C. Here b₁₁ is also the eigenvalue of B. If b₁₁ Î s (A), the system either has no solution or an infinity of solutions, verifying the assertion. Similar is the case when m = 1, when the system reduces to (B¢ - a₁₁I)X¢ = C¢ . Hence it is enough to assume the result for the sizes m-1 and n-1 and prove it for m, n. Since the field of complex numbers is algebraically closed, all complex matrices are triangulable. Let Y triangulize A and Z, B. Then we can write

,

,

.

In the above since the order of the elements along the diagonal of a triangular form is at our wish, we may assume that if s (A)Ç s (B) ¹ f , then a₁ Î s (B) and b₁ Î s (A).

If s (A)Ç s (B) = f , this system has a unique solution when looked at its rearrangement in N (­ ] ­ ) fashion:

T_A z - b₁ z = d, (solvable if b₁ Ï s (T_A) Ì s (A)),

(a₁ - b₁)x₁ + a¢ z = e₁, (solvable if a₁ ¹ b₁ ),

T_A X₁ - X₁ T_B - zb¢ = C₁, (solvable if a₁ Ï s (T_B) Ì s (B)),

a₁ x¢ + a¢ X₁ - x₁ b¢ - x¢ T_B = c¢ , (solvable if s (T_A)Ç s (A) = f ).

However, if f ¹ s (A)Ç s (B) э a₁, and the system has a solution, then any nonzero solution of x¢ (a₁I - T_B) = 0, i.e., of (a₁I - T_B¢ )x = 0, can be added to the "x" block to give rise to more than one solution. Hence either the system has no solution or more than one solution, completing the proof. #

Consider AX - XB = 0. If consistent Þ A²X = A(AX) = (AX)B = XBB = XB², A³X = XB³, and so on …, so that for any polynomial P, P(A)X = XP(B). In the non-uniqueness case X ¹ 0, and so we have f_B(A)X = 0, contradicting s (A)Ç s (B) = f . Conversely, if s (A)Ç s (B) ¹ f , let (l , x) and (l , y) be eigenpairs of A and B¢ respectively. Then X = xy¢ is a non-trivial solution of AX - XB = 0. #

Theorem. The matrix system AX - XB = C over a filed F is uniquely solvable iff (f_A, f_B), the HCF of the characteristic polynomials of A and B, equals unity.

PROBLEMS

.

,

Circulants and the Discrete Fourier Transform (DFT)

The discrete Fourier transform (DFT) matrix of order n is defined as F = (f_jk)₁£ j, , k£ n = ( n^-1/2 w ^{-(j-1) ( k-1)} ), where w is the n-th root of unity, w = exp(2p i/n) = exp(2p Ö (-1)/n). Note that F is symmetric, and for p, q = 1, 2, ... , n,

,

so that the DFT matrix F is a unitary matrix. Here we have used that for p ¹ q,

.

PROBLEMS

1. Show that the column vectors of the DFT matrix form a basis of C ⁿ that diagonalizes every circulant.

3. Show that the set of all circulants is closed under the operations of scalar multiplication, addition and matrix multiplication and consequently forms an algebra over C .

DFT of a Vector Signal and Solution of a Circulant System

Observe that with w _j = w ^j , j = 0, 1, ... , n-1,

,

and CF* = F* L , where L = diag (l ₀, l ₁, … , l _n-1), and

l _j = S ₀£ k£ n-1 c_k w _j^k, j = 0, 1, ... , n-1.

Hence C = UL U^*, (the spectral decomposition of a circulant) where U = F* is unitary. If L is non-singular, i.e. if C is non-singular then the solution of the circulant system

x = F* L ^-1 Fb = IDFT[DFT(b)/DFT(c)],

DFT º Ö n F,

IDFT º (1/Ö n) F* ,

(c₀ , c_n-1 , … , c₂ , c₁)¢

of C, as l _j = c₀ w _j⁰ + c₁ w _j¹ + … + c_n-2 w _j^n-2 + c_n-1 w _j^n-1 = c₀ w _j⁰ + c₁ w _j^-1 + … + c_n-2 w _j^-(n-2) + c_n-1 w _j^-(n-1). #

PROBLEMS

1. Determine the eigenvalues, range and the null space of the n´ n matrix

l -Matrices and Similarity

A square matrix A(l ) = (a_ij(l )) where the entries a_ij(l ) are polynomials in l over a certain field F (i.e., a_ij(l ) Î F[l ]) is called a l -matrix. We can write A(l ) = A_p l ^p + A_p-1 l ^p-1 + ... + A₁ l + A₀ where A₀, A₁, ... , A_p are square matrices with scalar entries from F and Bl ^k is to be interpreted as l ^kB (i.e., Bl ^k = (b_ijl ^k) = (l ^kb_ij), B = (b_ij)). A l -matrix is also called a matric polynomial in the indeterminate scalar l .

Thus A(l ) could be regarded as a polynomial in l with coefficients as matrices A₀, A₁, ... , A_p Î F^{n´ n}. If A_p ¹ 0, A(l ) is called a l -matrix of degree p (i.e., p = deg A(l )). A(l ) is called proper if the highest degree coefficient matrix A_p is non-singular. A(l) is called non-singular if F[l ] э det A(l ) ¹ 0. As a convention, the degree of the zero l -matrix is taken to be -¥ , i.e., deg (0) = -¥ . The rank of a l -matrix A(l ) is simply the rank of A(l ) regarded as a matrix over the field Q_F[l ].

If det A(l ) is a non-zero scalar, i.e., an element of F, there exists a l -matrix B(l ) such that A(l )B(l ) = B(l )A(l ) = I, the identity matrix. Here b_ij(l ) = (det A(l ))^-1 C_ji(l ), i, j = 1, 2, ... , n where C_ji(l ) is the (j, i)-th cofactor in A(l ). Thus if 0 ¹ det A(l ) is a scalar, (A(l ))^-1 is itself a l -matrix; whereas in general the entries in (A(l ))^-1 if det A(l ) ¹ 0, are elements of Q_F[l ], the field of fractions (rational functions) of F in the indeterminate l . Note that deg A(l ) = max_{i, j} {deg a_ij(l )}.

Lemma. If A(l ) is a proper l -matrix and B(l ) ¹ 0 is a l -matrix, deg (A(l )B(l )) = deg (B(l )A(l )) = deg A(l ) + deg B(l ).

Proof: We can write A(l ) = A_p l ^p + A_p-1 l ^p-1 + ... + A₁ l + A₀, 0 £ p B(l ) = B_q l ^q + B_q-1 l ^q-1 + ... + B₁ l + B₀ , 0 £ q where |A_p| ¹ 0 and B_q ¹ 0. Consequently A_pB_q and B_qA_p are non-zero matrices. As A(l )B(l ) = A_pB_q l ^p+q + ... + (S _i+j=k A_iB_j)l ^k + ... + A₀ B₀ and B(l )A(l ) = B_qA_p l ^p+q + ... + ( S _i+j=k B_jA_i)l ^k + ... + B₀A₀, the result follows. #

Corollary (degree reduction). If A(l ) is a proper l -matrix, C(l ) is a l -matrix, and B(l ) = A(l )C(l ), then deg B(l ) < deg A(l ) iff C(l ) = B(l ) = 0.

Proof: Else, by the Lemma deg B(l ) = deg A(l ) + deg C(l ) ³ deg A(l ) if C(l ) ¹ 0, a contradiction. #

Remainder Theorem (for l -Matrices) . If A(l ), B(l ) are l -matrices and B(l ) is proper, there exist unique l -matrices Q_l(l ), R_l(l ), Q_r(l), R_r(l ) such that Q_l(l )B(l ) + R_l(l ) = A(l ) = B(l )Q_r(l ) + R_r(l ), where deg R_l(l ), deg R_r(l ) < deg B(l ).

Proof: The uniqueness follows from Corollary 2, since, e.g., Q_l(l )B(l ) + R_l(l ) = Q(l )B(l ) + R(l ) implies that (Q_l(l )-Q(l ))B(l ) = R(l )-R_l(l ), and deg B(l ) > deg (R(l )-R_l(l )). The existence follows from the long-hand left and right division process. #

Theorem (Similarity via l -Matrices). Two n´ n matrices A and B are similar iff there exist l -matrices L(l ) and R(l ) such that |L(l )| and |R(l )| are non-zero scalars, and, L(l )(l I-A) = (l I-B)R(l ).

Proof: As l I-B and l I-A are first degree proper l -matrices, let L(l ) = (l I-B)R₁(l ) + C and R(l ) = L₁(l)(l I-A) + E, where C and E are scalar matrices. Then (l I - B)(R₁(l ) - L₁(l ))(l I - A) = l (E - C) + CA - BE. If R₁(l ) - L₁(l ) ¹ 0, the degree of left hand l -matrix is ³ 2 > degree of right hand l-matrix, a contradiction. Hence R₁(l ) = L₁(l ). It follows that E = C and CA = BE, so that CA = BC. It remains, therefore, to show that E = C is non-singular.

Since det (R(l )) is a non-zero scalar, (R(l ))^-1 is a l -matrix. Hence we can write (R(l )) = S₁(l )(l I-B) + S₂ (S₂ a scalar matrix). Then (R(l ))^-1R(l ) = I = (R(l ))^-1 (L₁(l )(l I-A) + E) = (R(l ))^-1L₁(l )(l I-A) + S₁(l )(l I-B)E + S₂E = (R(l ))^-1L₁(l )(l I-A) + S₁(l )C(l I-A)+ S₂E = ((R(l ))^-1L₁(l )+S₁(l )C)(l I-A) + S₂E, and unless (R(l ))^-1 L₁(l ) + S₁(l )C is zero, the degree of the right hand l -matrix would be ³ 1 ¹ deg (I) = 0. Hence S₂E = I and so E is non-singular. Note that the converse part is trivial, since if A = C^-1BC, we could choose L(l ) = R(l ) = C. #

PROBLEMS

1. Examine the proof of the previous theorem carefully so that if you are given two l-matrices L(l ) and R(l ) such that |L(l )| and |R(l )| are non-zero scalars and L(l )(l I-A) = (l I-B)R(l ), you could actually determine a C such that A = C^-1BC.

2. Construct appropriate l -matrices to check if the matrices

3. If A(l ), B(l ) are proper, show that A(l )B(l ) is proper.

4. Give an example of l -matrices A(l ) and B(l ) for which no two of deg (A(l )B(l )), deg (B(l )A(l )), and, deg A(l ) + deg B(l ) are equal.

Elementary Transformations on l -Matrices

The following three types of row (column) operations are called l -elementary row (column) operations on l -matrices, or just elementary operations, or transformations on l -matrices:

(iii) Adding to a row (column) a scalar polynomial in l times another row (column).

The operations (i)-(ii) are the same as the elementary row (column) operations discussed earlier. The difference lies in only the operation of type (iii) where here instead of just a scalar multiple we allow a more general l -polynomial multiple of a row (column) to be added to another.

A matrix obtained from the identity matrix by performing a l -elementary row (column) operation would be called an elementary l -matrix. It is interesting to note that every elementary l -matrix can be obtained by both a l -elementary row operation and a l -elementary column operation on an identity matrix. For, the three types of elementary l-matrices are:

, ,

Type (i) l -elementary matrix Type (ii) l -elementary matrix Type (iii) l -elementary matrix

and each type (i)-(ii) of a l -elementary row operation has the same effect on the identity matrix as the corresponding type of a l -elementary column operation. While adding a (l ) times the j-th row to the i-th row of I results in the same matrix as obtained by adding a (l ) times the i-th column to the j-th column.

As has been the case with the elementary row and column operations on a matrix, it follows that the rank of a l -matrix does not change by performing a succession of l -elementary row or column operations (as they constitute elementary row and column operations with respect to the field Q_F[l ]).

Two l -matrices are called equivalent if one of them can be obtained from the other by a succession of l -elementary row or column operations. Since the l -elementary row or column operations are reversible, it follows that this equivalence is actually an equivalence relation on the set of all l -matrices.

Theorem (Smith Normal Form). Every l -matrix A(l ) is equivalent to a l -matrix of the form diag (p₁(l ), p₂(l ), ... , p_r(l ), 0, ... , 0), where r = rank A(l ), and p_i(l ) are monic polynomials in l such that p_i | p_i+1 , i = 1, 2, ... , r-1.

Proof: Consider the lowest degree (non-zero) term in A(l ). If it does not divide every other term in A(l ), we show that A(l ) is equivalent to a matrix B(l ) in which the lowest degree term is of a lower degree than that in A(l ): For this, if a term which occurs in the same row or column as the lowest degree term a_ij(l ), say, is not divisible by a_ij(l ) we can subtract appropriate polynomial multiple of j-th column (or i-th row) from the column (row) containing the element to replace the element by a remainder of degree < deg a_ij(l ). Hence for the remaining cases we can assume that the i-th row and the j-th column contain only elements divisible by a_ij(l ). Now suppose a_pq(l ) is not divisible by a_ij(l ). First subtract appropriate polynomial multiple of i-th row from the p-th so as to make the (p, j)-th element zero and then add the i-th row so as to turn this element equal to a_ij(l ) itself. These operations only add a polynomial multiple of a_ij(l ) to a_pq(l ). Hence subtracting appropriate polynomial multiple of j-th column from the q-th column we can turn the (p, q)-th element to a remainder of degree less than deg (a_ij(l )), as required.

It follows from the above that using a succession of l -elementary row and column operations A(l ) is seen to be equivalent to a matrix in which the lowest degree term divides every other term. By an interchange of rows and columns this term could be brought to (1, 1)-position. Then subtracting appropritate polynomial multiples of the first row and column from the remaining rows and columns we can turn all other elements in the first column and row to zero. The remaining elements in the matrix continue to remain divisible by this (1, 1)-element. The matrix now is of the block-partitioned form

with p₁(l ) dividing every entry in B(l ). The polynomial p₁(l ) could be made monic by dividing the first row or column by the scalar coefficient of the highest degree term in it. Hence the result follows by an induction on the size of A(l ) and the fact that the l -elementary row and column operations do not change the rank of a l -matrix. #

Corollary. If det A(l ) is a non-zero scalar l -matrix, the Smith normal form of A(l ) is I, the identity matrix.

Proof: Since the l -elementary row and column operations change the determinant only by a non-zero scalar factor, it follows that in the present case no p_k(l ) can be of a degree > 1. Since the rank is full it follows that p_k(l ) = 1, for all k. #

The polynomials p₁(l ), p₂(l ), ... , p_r(l ) in the Smith canonical form of A(l ) are called invariant factors of A(l ). The following is a characterization of the invariant factors:

Theorem (Characterization Of Invariant Factors). If h_k(l ) denotes the HCF of all k´ k minors of a l -matrix A(l ) of rank r, the invariant factors p_k(l ), 1 £ k £ r, of A(l ) are given by p₁(l ) = h₁(l ), and p_k(l ) = h_k(l )/h_k-1(l ), 2 £ k £ r.

Proof: Consider a set (ordered in some form) of polynomials in l . It is clear that the HCF of this set is not affected by elementary operations of (i) interchanging the position of two elements in the set, (ii) multiplying an element by a scalar, and (iii) adding a polynomial multiple of one element to another. Next we have to note that when a l -elementary operation is performed on a l -matrix the set of the k´ k minors is affected only in one of the above fashions (i)-(iii) and consequently the HCF h_k(l ) remains invariant. Hence, as for the Smith normal form of A(l ) there hold h_k(l ) = P ₁£ i£ k p_i(l ), 1 £ k £ r, the result follows. #

Corollary. The Smith normal form of a l -matrix A(l ) is unique.

Proof: Since the h_k(l ) of the Smith normal form of A(l ) are the same as those of A(l ) itself, i.e., they are independent of the l -elementary row and column operations that brings A(l ) to this form, the result follows from the previous theorem which determine p_k(l ) uniquely in terms of the h_k(l ). #

To compute the invariant factors of a l -matrix, we could use the constructive procedure in the proof of the Smith normal form theorem, or else resort to the theorem on the characterization of the invariant factors via the HCF of minors of various size. Since, in this fashion, the invariant factors p_k(l ) of a l -matrix can be computed in a finite number of steps, the following result may be used to determine if two given matrices are similar:

Theorem. For two n´ n matrices A and B the following statements are equivalent:

(b) l I-A and l I-B have the same Smith normal form;

(c) l I-A and l I-B have the same invariant factors p_k(l ); and

(d) l I-A and l I-B are equivalent l -matrices.

Proof: It is clear that (a) Þ (b) Þ (c) Þ (d). Finally, if (d) holds we have L(l )(l I-A)C(l ) = (l I-B), where L(l ) is a product of elementary l -matrices corresponding l -row operations and C(l ) corresponds to the l -column operations that take l I-A to l I-B. Since both det L(l ) and det C(l ) are non-zero scalars, R(l ) = (C(l ))^-1 is a l -matrix and det R(l ) is also a scalar, (a) follows from a previous lemma. #

PROBLEMS

1. The invariant factors of l I-A, where A is the second of the following matrices, are l , l and l ² -4l :

.

2. Show that the determinant of a l -matrix A(l ) is a non-zero scalar iff A(l ) is a product of elementary l -matrices.

3. Find the inverses of the the three types of l -elementary matrices.

4. If D(l ) = det A(l ) ¹ 0, regarding A(l) as a matrix over the field Q_F[l ], show that (A(l ))^-1 is a l -matrix

iff D(l ) does not depend on l , i.e., it is a scalar.

5. Find the Smith normal form of l I-A for the following A's: