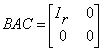 ,
,Chapter 3
CANONICAL FACTORIZATIONS
Given a linear system Ax = b, if a factorization of A, say of the form A = BC is known, the system may be written as a composite of the two systems of equations Bz = b and Cx = z, which, in some sense may be easier to solve (e.g., when B and C are triangular, unitary etc.), or the solution procedures for which may have some inherent advantage (e.g., less susceptibility to round-offs etc.). This is the basic motivation behind the various canonical matix factorizations below, the background for which must already be bamiliar.
1. Row-Reduced Echelon Form
Theorem. If A is an m
΄ n matrix over a field F, there exists an m΄ m non-singular B such that A = BE, where E is an m΄ n matix in a row-reduced echelon form.Proof: We already know that the row reduced echelon form of a matrix is unique and that it can be obtained via elementary row operations, a succession of which is equivalent to a pr-multiplication of the marrix by the corresponding elementary matrices. Thus, if E is the row reduced echelon form of A, we have CA = E, where C is a product of elementary matrices. Since a product of elementary matrices is non-singular, pre-multiplying by B = C-1, the result follows. #
2. Hermite Canonical Form
An n
΄ n matrix is said to be in Hermite canonical form if it is upper triangular, its diagonal entries are 0 or 1s, and if a 0 is a diagonal entry then the whole row is zero, and if a 1 is a diagonal entry then the rest of the entries in the same column are all zero. Such an H satisfies H2 = H (i.e., it is idempotent). For, if in the I-th row of H the diagonal entry is 1, the (I,j)-th entry in H2 is ai1a1j + ai2a2j + +aiiaij + + aikakj + + ainanj.Now if k
Ή I, and aik Ή 0, akk = 0 and so akj = 0 and consequently aikakj = 0 and if aik = 0, then any way aikakj = 0. Hence, since aii = 1, in the present case, the (I,j)-th entry in H2 is aij, which is the corresponding entry in H and therefore the I-th rows in H and H2 are identical. On the other hand, if aii = 0, the whole I-th row is zero in H, and so also in H2 and the I-th rows in H and H2 are identical. Hence, each row in H is identical to the corresponding row in H2 and the idempotence of H follows. #Theorem. Given any n
΄ n matrix A over a field F , there exist a non-sigular C and an H in Hermite canonical form such that A = CH.Proof: Start with the row-reduced echelon form. Permute rows to bring the leading unities to the diagonal. What results is a Hermite canonical form. #
Corollary. If Ax = b is consistent, x = Cb is a solution.
Proof: As Ax = b is consistent, for some z, b = Az. Since Cis non-singulr, premultiplying by C we find that Ax = b is equivalent to Hx = CAz. Hence we are to show that x = Cb = CAz is a solution of this. For this H(CAz) =H2z = Hz = CAz, and the proof is complete. #
Note that if H is idempotent, it is a projection and then if Hx = z is consistent, z
Î R(H) and so Hz = z, i.e., z = z is a solution of Hx = z. Also note that for any matrix K if its diagonal entries are either 0 or 1s, and if a 0 is a diagonal entry then the whole row is zero, and if a 1 is a diagonal entry then the rest of the entries in the same column are all zero, i.e., K satisfies all properties of a Hermite canonical form except for upper triangularity, still K satisfies K2 = K and if CA = K for some invertible C, a solution of a consistent Ax = b is given x = Cb.3. Rank Factorization
Theorem
. If A is an m΄ n matrix, there exist non-singular m΄ m B and n΄ n C such that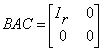 ,
,
where Ir is the identity matix of order r = r(A).
Proof: First reduce A to its row-reduced echelon form and then reduce the row-reduced echelon form to its column-reduced echelon form. Denoting the corresponding pre-multiplying matrix by B and the post-multiplying matrix by C, the resulting form is of the required type. #
4. Rank Factorization (Rectangular Form)
Theorem
. If A is m΄ n of rank r, there exist m΄ r E and r΄ n F, both of rank r such that A = EF.Proof: Using the previous result
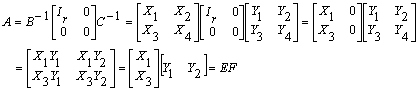
and E and F are m
΄ r and r΄ n, respectively, both of rank r as E has r independent columns and F has r independent rows. #
5. Rank Factorization (Left Invertible And Right Unitary)
Theorem
. Given an m΄ n complex matirx A of rank r there exists an invertible M and a unitary N such that with Ir denoting an identity matrix of order r![]() .
.
Proof: Apply Gram-Schimdt Orthonormalization process to rows of A and then permute the resulting rows so as to get the non-zero rows on the top. The operations involved are elementary row operations and the number of non-zero rows equals r = r(A). Denoting the corresponding pre-multiplying matrix by M-1:
![]() .
.
Completing Ur to an n΄ n unitary matrix by augmenting appropriate n r rows (e.g., by extending the set of row vectors to get a basis of " 1΄ n and then applying the Gram-Schimidt process) and calling the augmented matrix N one gets the desired result. #
Note that if A is real, the Gram-Schimdt process involves only real coefficients. Consequently, the matrices M and N in the above can be chosen to be real, which means that N is then an orthogonal matrix.
However, if A is not real N, in general, could not be taken to be orthogonal: for, as an example let, on the contrary,
. ![]()
Then, it is clear that both a and b cannot be real.
6. Triangular Reduction
Theorem
. If A is a square matix, there exists a non-singular B such that BA = U is upper triangular.Proof: The row reduced echelon form, for instance, does the job! #
7. Conjugate Diagonal Reduction of Hermitian Matrices
Theorem
. If A is hermitian, there exists a non-singular C and a real diagonal D such that A = CDC*.Proof: To begin with: (a) If a11 Ή 0, subtract appropriate multiples of the first column from all others (i.e., a1i/a11 times the first column from the i-th column) to sweep out the rest of the first row entries to zero. To sweep out the rest of the first column elements, subtract the corresponding conjugate multiples of the first row from the others (i.e., ![]() times the first row form the I-th row).
times the first row form the I-th row).
(b) If a11 = 0 and some ajj Ή 0, interchange the 1st and the jth rows and columns to turn (1,1)-th entry non zero and then proceed as before. (c) If every ajj = 0, and for some j, aj1 Ή 0, say aj1 = x + iy, (x, y real) add j-th row and columns to the first ones if x Ή 0 and add i = Ö (-1) times the j-th row and I times the j-th column to the first ones if x = 0 to get a real non-zero (1,1)-th element. Here also the pre and post multiplying matrices are adjoints of each other. With this non-zero (1,1) element proceed as before. (d) If none of the entries in the first row (and consequently in the first column) is non-zero, then nothing is to be done at the first stage.
In the second stage, proceed with a22 in the same fashion as done for a11 and so on with a33, , ann. The resulting diagonal matix is D and if E the product of the corresponding pre-multiplying matrices, since all the post multiplying matrices are adjoints of the corresponding pre-multiplying matrices at each stage we have EAE* = D. Writing C = E-1, the result follows. #
The same procedure in the real case gives rise to:
Corollary. If A is real symmetric there exist real non-singular C and diagonal D such that A = CDC’ .
8. Triangular Reduction by a Unitary Matrix
Theorem
. If a is m΄ n complex with m ³ n, there is a unitary B and an n΄ n upper triangular T such thatBA = ![]() ,
,
where 0, as usual, denotes a null matrix. If A is real, B can be taken to be orthogonal.
Proof: Rotate the first column of A in the direction of the first m-dimensional unit vector e1. Next consider the (m-1)
΄ (n-1) matrix obtained by removing the first row and column of the resulting matrix. Rotate its first column in the direction of (m-1)-dimensional e1, and so on .Finally combine the results:
![]()
9. QR-Decompostion
Theorem
. If A is m΄ n, m ³ n, A = QR where Q is m΄ n subunitary (Q*Q = In) and R is n΄ n upper-triangular.Proof: Via triangular reduction by a unitary matrix BA = (T | 0)
’ , with B unitary and T upper-triangular. From this one gets A = B*(T | 0)’ = QR, where R = T and Q consists of the first n columns of B*. As B* is unitary, Q*Q = In and of course R is upper-triangular. #10. Gram-Schmidt Triangular Reduction
Theorem
. If A is m΄ n, there exist n΄ n upper-triangular T and m΄ n S with its non-zero columns orthonormal such that A = ST, where for any s such that r(a) £ s £ min(m,n), precisely s columns of S could be managed to be non-zero.Proof: Apply Gram-Schmidt orthonormalization process to the columns of A from left to right. This is equivalent to post-multiplication of A by an n
΄ n upper-triangular matrix E which is non-singular: AE = F, where non-zero columns of F are orthonormal. Thus A = FE-1 = FG, where G = E-1 being inverse of an upper-triangular matrix is upper-triangular. Note that r(a) = r(F) and so precisely r(A) columns of F are non-zero. These non-zero columns can be augmented with m-r extra vectors to make an orthonormal basis of C m (R m). Then any zero column(s) of F could be replaced by these augmenting vectors and the corresponding row(s) of G replaced by zero row, so long as the total number s of non-zero columns in modified F does not exceed min(m,n). Calling modified F, G respectively by S, T we have the result. #11. Simultaneous Reduction of Positive Definite A and Hermitian B
Theorem
. Let A be positive definite and B Hermitian. Then there exists a non-singular C such that C*AC = I and C*BC = D, where D is a diagonal matrix.Proof: Let Q = P-1 where P = Ö A. Note P and Q are Hermitian. Now, (Q*BQ)* = Q*B*Q = Q*BQ. Hence there is a unitary U and a diagonal D such that U*Q*BQU = D, i.e., (QU)*B(QU) = D and (QU)*A(QU) = U*Q*AQU = U*Q*(QQ*)-1QU = U*Q*Q*-1Q-1QU = I. Thus, C = QU is a desired matrix. #
12. Non-Singular LU-Decompostion
Theorem
. Let A be a square matrix. Then there exist respectively lower and upper triangula non-singular matrices L and U such that A = LU iff all principal submatrices of A are non-singular.Proof: Let A be n΄ n and let Ak denote the k-th principal submatrix of A (obtained by deleting the last n-k rows and columns of A). Since Ak = LkUk, the necessity follows. Next, let |Ak| Ή 0, k = 1, 2, , n. The result is true for 1΄ 1 matrices and so assume it for (n-1)΄ (n-1). Then we can write for some Ln-1 and Un-1 of the required type An-1 = Ln-1Un-1.
Consider the equation
![]()
i.e., An-1 = Ln-1Un-1, a = Ln-1t, bT= yTUn-1,
a = yTt+g d . Of these the first relation is true by the induction hypothesis and the last three are equivalent to t = (Ln-1)-1a, yT = bT(Un-1)-1, and g d = a -bT(An-1)-1a. Note that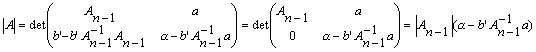 .
.
Thus, g d = |A|/|An-1| Ή 0, and so non-zero g , d can be chosen and we have the required result for n΄ n matrices, completing the proof. #
PROBLEMS
1
. If L1U1 = L2U2, where L1, L2 are lower triangular, U1, U2 upper triangular and all are non-singular, show that there exists a non-singular diagonal matrix D such that L1 = L2D, U1 = D-1U2.2. Prove that A possesses a non-singular LU decomposition iff there exist a lower triangular L, an upper triangular U, both with diagonal elements 1 (such triangular matrices are called unit triangular matrices) and a non-singular diagonal matrix D such that A LDU. Show also that the L, D and U are uniue.
3. Can you characterize the matrices A that can be written as LU where L and U are respectively lower and upper triangular, but are not necessarily non-singular?
4. If A is non-singular, show that there exists a permutation matrix P such PA has an LU decomposition.
5. When does a non-singular A have a UL decompostion, where U is upper triangular and L a lower triangular matrix?
13. Cholesky LL*- Decompostion
Theorem
. A = LL* for some lower triangular and non-singular L iff A is positive definite.Proof: The necessity is clear as L is to be non-singular. For the sufficiency, the result is obvious for 1΄ 1 matrices and so assume it for (n-1)΄ (n-1) matrices. Then we can write An-1 = Ln-1(Ln-1)*. Set up the system:
![]()
i.e., An-1 = Ln-1(Ln-1)*, a = Ln-1y, a* = y*(Ln-1)* and
a = y*y + |g |2. The middle two relations here are equivalent to y = (Lk)-1a. since![]()
we have
a -y*y = |A|/|An-1| > 0, and so g can also be chosen. #Corollary. A Hermitian A is positive definite iff |Am| > 0, 1
£ m £ n, where Am denotes the principal m΄ m submatrix of the n΄ n A.Proof: If A is positive definite A = LL* and so Am = Lm(Lm)*
Þ |Am| = | Lm||(Lm)*| = |det(Lm)|2 > 0, as Lm is non-singular, m = 1, 2, , n. Conversely, if |Am| > 0, m = 1, 2, , n, the proof of the sufficiency part of LL*-decompostion is valid. So, A = LL* with L non-singular. Then for x Ή 0, (Ax,x) = (LL*x,x) = (L*x, L*x) ³ 0. Thus A is positive definite. #PROBLEMS
1
. Is LL* decomposition unique?2. Can LL* decomposition be obtained by using only (+, -, ΄ , /) arithmetic operations?
3. If A is positive definite, show that there exist unit lower triangular L and a positive diagonal matrix (a diagonal matrix with positive diagonal elements) D such that A = LDL*.
4. Can LDL* decompostion be obtained by using only (+, -, ΄ , /) arithmetic operations? Are L and D unique?
5. Can every positive semi-definite matrix be written as LL* where L is lower triangular but not necessarily non-singular?
14. Singular Value Decomposition (SVD)
Let A be m
΄ n of rank r. Let m 1, m 2, , m r be the non-zero common eigen-values of AA* and A*A. Let l I = Ö m I, I = 1, 2, , r. Put n I = (1/l i)A*ui, I = 1, , r. Then: (vj)*vi = (1/l j) (1/l i)(uj)*AA*ui = (l i/l j)(uj)*ui = d ij, and A*Avi = (1/l i)A*AA*ui = l iA*uI = m Ivi. Complete {v1, v2, , vr, vr+1, , vn} to be an orthonormal (unitary) basis of C n. Then, vis are orthonormal eigenvectors of A*A corresponding to the n eigenvalues m 1, m 2, , m r, 0, 0, , 0. By symmetry (interchanging the roles of A and A*), (1/l i)Avi = wi, I = 1, 2, , r are orthonormal eigenvectors of AA* for eigenvalues m 1, m 2, , m r. Indeed here wi = ui, for: wi = (1/l i)Avi = (1/l i)A(1/l i)A* ui = (1/m i)AA* ui = ui.Now let {u1, u2, , ur, ur+1, , um} be an orthonormal basis of
C m. Then AA*uj = 0 for j ³ r and so also A*uj = 0 for j > r. Hence post-multiplying the identity![]()
by A we have
![]() .
.
Hence the SVD:
Theorem. If A is an m΄ n complex matrix of rank r, there exist unitary U and V and L = diag (l 1, l 2, , l r), an r΄ r diagonal matrix with positive diagonal entries l i, 1 £ i £ r, such that
![]() ,
,
where ui and vi denote the i-th columns of U and V respectively. #
PROBLEMS
1
. Prove that the singular values of a square A are precisely the magnitudes of the eigenvalues of A iff A is normal.2. Let A be normal and UDU* its unitary diagonalization. Prove that an SVD of A is given by UL V*, where L = |D| and V = U|D|-1Ð .
3. Find the SVD of the matrices:
(2), (1 3), (1 2 3), (1 2 3 4), (1 2 3)’ , ![]() .
.
15. Polar Decomposition
Theorem
. If A is m΄ n of rank m, there exists a positive-definite matrix P and a sub-unitary V such that A = PV*.Proof: Here the matrix AA* is m
΄ m positive definite. Let P = Ö (AA*) be the positive definite square root of AA*. Put U = P-1A. Then U is m΄ n and U*U = ((Ö (AA*))-1A)*( Ö (AA*))-1A = A* (Ö (AA*))-1 ( Ö (AA*))-1A. Hence UU* = (Ö (AA*))-1AA*( Ö (AA*))-1A = I, so that the rows of U are orthonormal, i.e., U* is sub-unitary (B is sub-unitary if B*B = I). Hence with V = U*, we have the result A = PU = PV*. #If m = n, i.e., A is square, then so is U and so U is unitary and we have the polar decompostion:
Theorem. If A is a non-singular matrix, there exist positive-definite P and unitary U such that A = PU, (P =
Ö (AA*)). If, in addition, A is real, then P is real symmetric and U is orthogoanl, i.e., P and U can be chosen to be real.If A is not of full rank, let Ak = PkUk. {Uk} is a bounded sequence, its rows being normalized. Hence there is a convergent subsequence, which w.l.g. we could take to be the sequence itself, Uk
® U. Then Pk = AkUk* ® AU* = P, say. (Here sub-unitariness of U* has been made use of). The matrix P, being a limit of positive definite matrices is positive semi-definite at worst. As U is a limiting case of Uks, U* is subunitary and A = PU. Hence:Theorem. If A is m
΄ n, and m £ n, there is a positive semi-definite m΄ m P and a sub-unitary n΄ m V such that A = PV*. If A is real P and V could in addition be chosen to be real, i.e., P as real symmetric and V as sub-orthogonal. Also, if A is of full rank (m) then P is positive definite. #Exercise: Is the above result true for m > n?
Applying the result to A*, we get A* = PU*, say, so that A = UP* = UP, so that we have:
Theorem. If A is m
΄ n, m ³ n, there exist a positive semi-definite n΄ n P and a sub-unitary m΄ n U such that A = UP. If A is real, in addition P is real symmetric and U is sub-orthogonal. If A is of rank n then P is positive definite. (Note: P = Ö (AA*)).Also it follows from the above that for a square matrix A both the types of polar decompositions PU and VQ hold.
To avoid the little unpleasantness in writing as well as remembering A = UP, m
³ n and A = PV*, m £ n, where U and V are sub-unitary and P p.s.d., we could generalize the definition of a sub-unitary matrix to the following: Call U sub-unitary if either UU* = I, or U*U = I. It then is indeed clear that if U is m΄ n sub-unitary, the former holds iff m £ n; the latter iff m ³ n; and that U is unitary iff m = n. Now the polar decomposition simply reads as follows:Any m
΄ n complex matrix A can be written as A = PU if m £ n, and A = UP if m ³ n, where P is positive semi-definite and U is subunitary. Moreover, P and U could be chosen to be real iff A is real.PROBLEMS
1
. What are polar dedompositions of a positive definite matrix P, a unitary matrix U and the matrices UPU and PUP, with P and U as before.2. Let A be normal and UDU* its unitary diagonalization. Find a polar decomposition of A.
3. Find polar decomposiitons of the matrices:
(2), (1 3), (1 2 3), (1 2 3 4), (1 2 3)’ , ![]() .
.
16. When do the Polar Factors Commute?
Let A be square and A = PU be its polar decomposition. Suppose P2 and U commute. Then A*A = (PU)*PU = U*P*PU = U*P2U = U*UP2 = P2 = (
Ö (AA*)2 = AA*, and hence A is normal.Conversely, let A be normal and A = PU be its polar decomposition. Then (PU)*PU = PU(PU)*
Þ U*P2U = P2 Þ P2U = UP2. Hence P2 commutes with U. But a positive semi-definite matrix P commutes with U iff P2 commutes with U (in fact if any positive power of P commutes with U use Müntz-Szasz theorem, or use Weierstrass approximation theorem to approximate Ö x by Pm(x) and so x by Pm(x2)). For, let V be a unitary diagonalizer of P: V*PV = D Þ P = VDV*. Then P2U = UP2 Þ VD2V*U = UVD2V* Þ D2V*UV = V*UVD2 Þ D2C = CD2, where C = V*UV. Comparing (i,j)-th terms on both sides (di)2cij = cij(dj)2. If cij Ή 0, Þ (di)2 = (dj)2 Þ di = dj (both being non-negative, P being positive semi-definite) Þ dicij = cijdj and this remains valid trivially also in case cij = 0. Þ DC = CD Þ PU = UP. Hence we have:Theorem. Let A = PU be a polar decomposition.Then A is normal iff the polar factors P and U commute. (The same result is valid for the decomposition A = UP of second type.)
17. Unicity of Polar Decomposition
If A = PU, AA* = PUU*P = P2 and so P, being positive semi-definite, is the unique square root of AA*. Hence, it follows that if A is non-singular the polar decomposition is unique. [Taking A = 0, it is clear that in the singular case the decomposition may not be unique].
Equivalence of Polar Decomposition and SVD
Let A be m
΄ n and A = PW* (or WP), where P is p.s.d. and W is sub-unitary. Writing P = YL Y*, A = YL Y*W*. Since, for V* = Y*W*, V*V = Y*W*WY = Y*Y = I, V is sub-unitary and A = UL V*, U unitary, V sub-unitary. In the m ³ n case, similarly A = WP = WYL Y* and with U = WY, U*U = Y*W*WY = I Þ U is sub-unitary. Hence A = UL V* with V = Y and U sub-unitary. Hence SVD is a corollary of polar decomposition.Conversely, given SVD of A, A = U
L V* (U extended to become unitary) (V sub-unitary), A = (UL U*)UV* = PW*, say, where P = UL U* is p.s.d. and W*W = UV*VU* = UU* = I, and WW* = VU*UV* = VV*, i.e., A = PW is a polar decomposition. Hence polar decomposition is a corollary of SVD. Thus the polar decomposition and the SVD are equivalent. #
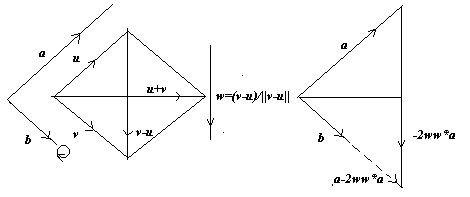 To Rotate a Vector in the Direction of Another Vector
To Rotate a Vector in the Direction of Another Vector
The Complex Case
: Let a and b be two non-zero vectors in an inner product space. We sish to construct a reflection matrix (a unitary matrix) U which flips a given vector a Î C n in the direction of another vector b Î C n. If (a,b) = reiq is not zero, let u = a/||a|| and v = eiq b/||b||. (If (a,b) is zero choose q in above to be zero. Now (u,v) is real non-negative. If v-u is zero, the unitary matrix v = e-iq I takes a into e-iq a = e-iq ||a||u = e-iq ||a||v = e-iq ||a||eiq b/||b|| = (||a||/||b||)b, which is in the direction of the vector b. If v-u is non-zero, let w = (v-u)/||v-u|| and U = e-iq (I-2ww*). Since w is a unit vecor, U*U = eiq (I-2ww*)e-iq (I-2ww*) = I 4ww* + 4ww*ww* = I, i.e., U is unitary. Now, (u+v,u-v) = ||u||2 - ||v||2 (u,v) + (v,u) = 0, since ||u|| = ||v|| and (u,v) = (v,u) as (u,v) is real. As (u-v,u-v) = ||u-v||2, we have (u,u-v) = [(u+v,u-v) + (u-v,u-v)]/2= ||u-v||2/2. Finally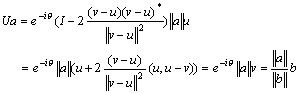 . #
. #
The Real Case: If x, y Î R n, let (I-2ww’ )x = P xP y/P yP . Then, P yP x - P xP y = 2(w’ x)w. Now, 0 = P yP x’ x - P xP y'x is equivalent to y’ x = P yP P xP , which happens iff x is a positive scalar multiple of y, in which case the identity operator flips x in the direction of y. If x is not a positive scalar multiple of y, taking
w = [P yP x-P xP y]/P [P yP x-P xP y]P ,
and putting c = P [P yP x - P xP y]P , c2 = P [P yP x - P xP y]P 2 = 2P yP 2P xP 2 - 2P xP P yP y’ x =2P yP P xP [P yP P xP - y’ x],
(I-2ww’ )x = x - 2[P yP x - P xP y] [P yP x’ x-P xP y’ x]/c2 = x - 2[P yP x - P xP y]P xP [P yP P xP -y’ x]/c2
= [1 - 2P yP P xP [P yP P xP - y’ x]/c2]x + 2P xP y]P xP [P yP P xP -y’ x]/c2 = [P xP /P yP ]y].
Flipping in the Direction of the First Unit Vector: For x Î R n, we have the flip as [I - 2ww’ ], where
w = [x - P xP e1]/[2P xP (P xP -x1)]1/2.
For x Î C n, if x1 = 0, the flip is [I - 2ww* ], where
w = [x - P xP e1]/[ P xP Ö 2];
and, if x1 Ή 0, put z = (|x1|/x1)x, the flip is (|x1|/x1|)[I - 2ww* ], where
w = [z - P zP e1]/[2P zP (P zP -z1)]1/2.
20. Tridiagonalizing a Hermitian Matrix by Householder Reflections
Let A be n
΄ n hermitian. We can choose a Householder transformation U1 = (I-2ww*) Î C (n-1)΄ (n-1) such that U1 rotates the first column vector (a21, a31, , an1)’ parallel to the vector (1, 0, 0, , 0)’ Î C n-1. Then![]()
is a unitary matrix such that
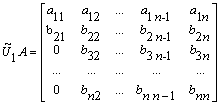 .
.
Since Ũ1 does not affect the first row on pre-multiplication Ũ1* does not affect the first column on postmultiplication. Hence Ũ1AŨ1* being hermitian has the form
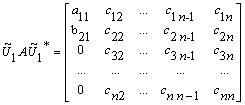 .
.
The same idea can now be continued via Ũ2 = diag (1, 1, U2), U2 Î C (n-2) ΄ (n-2) and so on till Ũn-1 = diag (1, 1, , Un-2), so that we end up in a tridiagonal hermitian matrix Ũn-2 Ũ2Ũ1Ũ1AŨ1*Ũ2* Ũn-2*. Note that the Householder rotation U which rotates (x1, x2, , xn)’ in the direction of the first unit vector (1, 0, , 0)’ is given by U = e-iq (I-2ww*), where w = (v-u)/||v-u||, q = arg (x1), u = x/||x||, and v = eiq (1, 0, 0, , 0)’ . #
21. QR-Algorithm for Hessenberg Matrices
(a) If As is upper-Hessenberg, Qs orthogonal and Rs upper triangular such that QsAs = Rs, then As+1 = RsQs
’ = QsAsQs’ need not be upper Hessenberg as the following counter example shows:Counter Example: Let
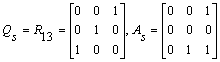 .
.
Then
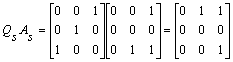
is upper-triangular. But
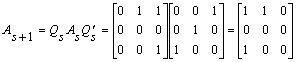
is not upper-Hessenbrg (i.e., the entries below the first sub-diagonal are not all zero).
(b) If As is a non-singular and upper Hessenberg matrix and QsAs = Rs, where Qs is unitary and Rs is upper-triangular, then As+1 = RsQs* = QsAsQs* is upper-Hessenberg.
Proof: Rs is non-singular. Then As = Qs* Rs implies the 1-st column of Qs* is of the form (x, x, 0, 0, , 0, 0)
’ . Þ the 2-nd column of Qs* is of the form (x, x, x, 0, , 0, 0)’ . Þ Þ (n-2)-th column of Qs* has the form (x, x, x, x, , x, 0)’ . Þ Qs* is upper-Hessenberg. Þ RsQs* is upper-Hessenberg as Rs is upper-triangular. #(c) Let As be upper-Hessenberg. Then there exist Qs unitary (orthogonal, if As is real) and Rs upper-triangular such that QsAs = Rs and As+1 = RsQs* = QsAsQs* is upper-Hessenberg.
Proof: Let As be upper-Hessenberg. If As is non-singular for all k sufficiently large, As(k) = As + I is non-singular and upper-Hessenberg. Hence via Householder triangulization there exist Qs(k), Rs(k), respectively unitary and upper-triangular such that: (1) Qs(k)As(k) = Rs(k). Then by (b): (2) As+1(k) = Rs(k)(Qs(k))* = Qs(k)As(k)(Qs(k))* is upper-Hessenberg for all k as above. Since Qs(k)s are unitary they have a subsequence along which they have a unitary limit Qs, say. Taking limit in in (1) along this sequence we have QsAs = Rs, an upper-triangular matrix (the limit of Rs(k) exists via the left hand side). Hence also As+1 = lim As+1(k) exists and we have As+1 = RsQs* = QsAsQs*, an upper-Hessenberg matrix (as a limit of a sequence of upper-Hessenberg matrices). #