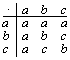
Chapter 4
VECTOR SPACES
1. Vector Space over a Field
A vector space V over a field F is a non-empty set V (whose elements are called vectors) along with two operations "+" (vector addition) and "Χ " (scalar multiplication, which is generally omitted in writing) such that: + : V ΄ V ® V , and Χ : F ΄ V ® V , satisfying for any x, y, z Î V and a, b, c Î F the axioms:
(1) x + y = y + x, (commutativity);
(2) x + (y + z) = (x + y) + z, (associativity);
(3) there is an element 0 (called zero vector) in V such that: x + 0 = x;
(4) for each x Î V there is an element -x Î V (negative, or additive inverse of x) such that x + (-x) = 0;
(5) a(bx) = (ab)x, (associativity of scalar multiplication);
(6) a(x + y) = ax + ay (distributivity of scalar multiplication over vectors);
(7) (a+b)x = ax + bx (distributivity of scalar multiplication over scalars);
(8) 1.x = x, where 1 is the multiplicative identity of F .
If W is a subset of a vector space V and under the operations "+" and "." of V , W itself is a vector space, we call W a vector subspace or just a subspace of V . It is obvious that W is a subspace of V iff W is closed under the operations "+" and "Χ " of V .
If S is a subset of a vector space V , span{S }, written as <S > is the smallest subspace of V containing S and is called "span of S " or the "subspace generated or spanned by S ".
Theorem. <S > is precisely the set of all possible linear combinations of elements of S .
Proof: The set of all possible l.c.s of elements of S is a subspace of V . Also any subspace of V that contains S contains all l.c.s of elements of S . Hence the set of all l.c.s of elements of is the smallest subspace of V containing S . #
Examples: (a) F n, n = 1, 2, ... , ₯ , the set of n-component column vectors x = (x1, x2, ... , xn), xi Î F , a field, with componentwise addition and scalar multiplication : x + y = (x1+y1 , x2+y2 , ... , xn+yn ), cx = (cx1, cx2, ... , cxn), is a vector space over the field F . The same applies to the space F (n) of n-component row vectors (called n-tuples): x = (x1, x2, ... , xn), xi Î F . If n = ₯ , we get F (₯ ) , the vector space of all infinite sequences.
(b) R over R , C over C , C over R , with usual addition and multiplication.
(c) R 2, the set of planar vectors over R , R 3 the set of 3-dimensional Euclidean space vectors over R with the standard vector addition and scalar multiplication.
(d) The subspace of F consisting of all infinite sequences in which all but a finite number of terms are zero can be identified with the vector space P Ί F [x] of all polynomials in an indeterminate x over the field F . For this we take x = (0, 1, 0, 0, ... ), x0 = (1, 0, 0, 0, ... ), x2 = (0, 0, 1, 0, ... ), ... , xk = (0, 0, ... , 0, 1,0, ... ), k = 1, 2, 3, ... , where the (k+1)-th element in xk is 1 and the rest are zero. Then (c0, c1, c2, ... , cn, 0, ... ) Ί c0 +c1x+c2x2+c3x3 +...+cnxn, a polynomial of degree n in x. The powers of x follow the general rule of Cauchy product of two sequences {an} and {bn} as the sequence {cn}, where n = 0, 1, 2, ... and cn = S 0£ k£ n akbn-k = a0bn + a1bn-1 + a2bn-2 + ... + anb0.
Using the notion of the indeterminate x = (0,1,0,0,0, ... ), the space F ₯ itself can be realized as the space of all formal power series f(x) = c0 + c1x + c2x2 + ... + cnxn + ... .
It follows from the associativity of vector addition that the sum v1 + v2 + v3 + ... + vk Ί ((( ... ((v1 + v2) + v3) + ...) + vk-1) + vk) can be evaluated by inserting the brackets (grouping the terms) in any fashion one likes. If v = c1 v1 + c2 v2 + ... + ck vk , ci Î F , vi Î V , we call v a linear combination (l.c.) of v1, v2, ... , vk. The l.c. is called non-trivial if at least one scalar ci is different from zero. Similarly, a homogeneous linear relation c1v1 + c2v2 + ... + ckvk = 0, ci Î F , vi Î V , is called non-trivial if at least one ci is non-zero.
PROBLEMS
1. If a Î F , v Î V (F ) and av = 0, show that at least one of a or v is zero.
2. The set {0} consisting of the singleton 0 is the intersection of all subspaces of a vector space.
3. Let F = Z p , the field of integers modulo p. Determine those p for which the set of all vectors x Î F 2 for which x12 - x22 = 0, is a subspace of F 2.
4. If X , T are subsets of a vector space V and <T > Ì <X > is it true that T Ì X ?
5. Verify that the zero of a subspace of a vector space must be the zero of the vector space itself.
6. Determine a1, a2, ... , an and a Î F such that the set S = {x | a1x1 + a2x2 + ... + anxn = a}is a subspace of F n. Show that, for any a Î F , if one member u of S is subtracted from all members of S , the resulting set S -u, say, is always a subspace.
7. If U and W are subsets of a vector space V over F , z Î V and c Î F , one defines: cU = {cx | x Î U }, z + U = U + z = {u+z | u Î U }, U + W = {u+w | u Î U , w Î W }, F U = {cu | c Î F , u Î U }.
Following the convention that: 2 = 1 + 1, 3 = 2 + 1, -2 = -(2) and so on, in any field F , is W + W = 2W true for every subset W ? Is it true that if W is a subspace of V then mW = W + ... + W (m-times)?
8. Show that W is a subspace of V iff F W = W and W + W = W .
9. Show that W is a subspace of V iff F W = W and W - W = W .
10. Show that W is a subspace of V iff W = F W - W .
11. If X and Y are subsets of a vector space V and <X > Ç <Y > Ή {0}, then X Ç Y Ή f .
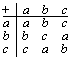
12. Verify that the set F = {a,b,c}, together with + and ΄ as in

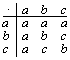
is a field. Identify the "0", "1", "b ", "c ", "-b" and "-c" elements and determine the nuber of elements in F n?
13. In connection with the span of a set S , why does one work only with the finite linear combinations? What is the difficulty in considering infinite linear combinations? Discuss when the field F is general? What if the field is that of rational numbers, real numbers, complex numbers, or is the field of integers modulo a prime p?
14. Consider the subset (F ₯ )0 of F ₯ of sequences having at the most a finite number of non-zero elements. Explain why <(F ₯ )0> Ή F ₯ .
15. What is the span of the set of all convegent complex sequences in C ?
16. Determine the span of all complex sequences converging to 1? Does it contain the span of all complex null sequences (i.e., converging to 0)?
17. Describe the following subsets of R 3 pictorially: (a) {x | x12 + x22 + x32 = 1}; (b) {x | x12 + x22 - x32 = 1}; (c) {x | x12 - x22 - x32 = 1}; (c) {x | x12 - (x2 + x3)2 = 0}. What do these represent? Determine their spans?
18. What are all possible subspaces of R 1 , R 2 , 3 over R ?
19. Show that if W is a subset of a vector space V over a field F such that au + v Î W for all u, v Î W and a Î F then W is a subspace of V .
20. If W 1, W 2, ... , W k are subspaces of a vector space V , prove that W = W 1 + W 2 + ... + W k = {w1 + w2 + ... + wk : wi Î W i, 1 £ i £ k} is the smallest subspace of V containing each W i. (W is called the sum of the subspaces W i s.)
21. If V 1, V 2, ... , V m are vector spaces over a field F and V denotes the cartesian product V 1΄ V 2΄ ... ΄ V m = {(v1, v2, ... , vm) : vi Î V i}, show that V is a vector space over F under the so called componentwise vector addition and scalar multiplication given by c(v1, v2, ... , vm) = (cv1, cv2, ... , cvm), and (u1, u2, ... , um) + (v1, v2, ... , vm) = (u1+v1, u2+v2, ... ,um+vm).
22. If C is the field of complex numbers, think about the possible ways of describing the set W =span {(1,2,3),(4,5,6), (7,8,9)} in C 3. The obvious answer following from the definition is that W consists of vectors of the form v = (a+4b+7c,2a+5b+8c,3a+6b+9c)’ , where a, b, c Î C are 3 arbitray parameters. Is there a simpler description? Show that none with less than 2 parameters will do.
23. Let V be the set of all pairs (x,y) of real numbers, and let F be the field of real numbers. Define (x,y) + (z,t) = (x+t,y+z) and c(x,y) = (cx,cy). Is V , with these operations, a vector space over the field of real numbers?
24. Define two operations "Å " and "· " on R n by a Å b = a - b and c· a = -ca , where the operations on the right are the usual ones. Which of the axioms for a vector space are violated by (R n, Å , · )?
25. Let V be the vector space, over R , of all complex-valued functions f on the real line with the usual addition and scalar multiplication of functions and let W denote the set of g Î V satisfying
![]() ,t Î R .
,t Î R .
Verify that W is a subspace of V and that any f Î V can be uniquely written as g+ih, with g, h Î W .
26. If V is a vector space over a field F , which of the following sets of vector addition and scalar multiplication operations on the cartesian product X = V ΄ V turn it into a vector space over F ? (a) (x, y) + (z, t) = (x+z, 0), and, c(x, y) = (cx, 0); (b) (x,y) + (z,t) = (x+z, -y-z), and, c(x,y) = (cx, -cy);
(c) (x, y) + (z, t) = (y+t, x+z), and, c(x, y) = (cy, cx); (d) (x, y) + (z, t) = (x+z, y+t) and c(x, y) = (cx, cy).
27. Which of the following sets of vectors v = (x, y, z, t)’ define subspaces of the vector space C 4 over C ? (a) all v such that Re (x + y + z + it) = 0; (b) all v such that x + y + z = it; (c) all v such that x = y and x = -y; (d) all v such that x + y + z = t; (e) all v such that x2 + y2 + z2 = t2; (f) all v such that t is rational.
28. Let V be the vector space over R of all real functions f from R into R with the usual addition and scalar multiplication. Which of the following sets of functions are subspaces of V ? (a) all f such that f(x2) = f(-x), x > 0; (b) all f such that f(0) = f(1) + f(-1); (c) all odd f such that f(69) = f(-69); (d) all f such that f(-8) = -8; (e) all f which are not continuous; (f) all even f whose square is odd; (g) all bounded and differentiable f each of whose first derivative vanishes at least at one point.
29. Which of the vectors (1, 2, 3, 4)’ , (1, -1, -1, 1)’ and (1, 1, 1, 1)’ lie in the span of (1, -1, 0, 0), (0, 1, 1, 0)’ and (0, 0, 1, -1)’ in R 4? If S denotes the set of all (w, x, y, z, t)’ Î R 4 satisfying
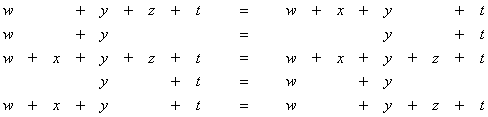 ,
,
show that the span of the set S is S itself, and also that there exists a finite subset of S which spans S .
30. Let V = R n΄ n. Which of the following sets of matrices A in V are subspaces of V ? (a) all A such that A+cI is invertible for some c Î R ; (b) all A such that A+cI is non-invertible for some c Î R ; (c) all A such that AB+BA = 0, B being a fixed matrix in V ; (d) all A such that A2 = 2A; (e) all A such that A’ = A. Now answer the same question when V = F n΄ n, F being some field.
31. Let a subspace W of a vector space V be called non-trivial if W Ή {0}, V . Regarding R 1 as a straight line, R 2 as a plane, and R 3 as the euclidean three dimensional space, verify that : (a) R 1 has no non-trivial subspace; (b) straight lines passing through the origin are the only non-trivial subspaces of R 2 ; and (c) W is a non-trivial subspace of R iff either it is a straight line passing through the origin or that it is a plane passing through the origin.
32. If S and W are subspaces of a vector space V prove that the set-theoretic union S È W is a subspace of V iff one of S or W contains the other. Does the result generalize to a finite union of subspaces? Does it generalize to an infinite union?
33. Let V denote the vector space of all real valued functions defined in the plane, S the subset of functions f Î V which are symmetric about the origin (i.e., f(P) = f(-P)) and let A consist of all functions f in V which are antisymmetric about the origin (i.e., f(P) = -f(-P)), . Prove that : (a) S and A are subspaces of V ; (b) S + A = V ; and (c) prove that S Ç A = {0}.
34. If W 1 and W 2 are subspaces of a vector space V , show that the following two statements are equivalent: (i) for each v Î V , there exist unique vectors w1 Î W 1 and w2 Î W 2 such that v = w1 + w2; and (ii) W 1 + W 2 = V and W 1 Ç W 2 = {0}.
35. In R 4, let S denote the totality of vectors (x, y, z, t) for which t -x -y -z = 1. What is the subspace <S >?
2. Linear Independence of Vectors
A set S of vectors is called independent or linearly independent if there exists no non-trivial homogeneous relation between elements of S , i.e., c1v1 + c2v2 + ... + ckvk = 0, ci Î F , vi Î S Þ c1 = 0 = c2 = ... = ck . Thus if S is independent, a homogeneous relation in S must be trivial. A set which is not linearly independent is called linearly dependent or simply dependent. If S is l.i. (l.d.) we call the elements of S themselves as l.i. (l.d.).
The unit vectors e1 = (1, 0, 0, ... , 0), e2 = (0, 1, 0, ... , 0), e3 = (0, 0, 1, ... , 0), ... , en = (0, 0, 0, ... , 1) in F (n) are linearly independent. Non-zero row vectors of a matrix in row-reduced echelon form are l.i. in the vector space of row vectors of the same size. The monomials {1, x, x2, x3, ... } constitute a l.i. subset of the vector space of polynomials.
PROBLEMS
1. The nature of linear dependence or independence of an ordered set of vectors does not change under any of the following three types of operations: (i) multiplying a vector by a non-zero scalar, (ii) adding a scalar multiple one vector to a different vector, and, (iii) interchanging the position of two vectors!
2. Any set of n+1 or more vectors in F n is linearly dependent!
3. Prove that any given three vectors in R 3 are linearly dependent iff they are co- planar. What would be the corresponding statement in R 1 and R 2? What about R n?
4. Consider a plane in R 3. Take three points P, Q and R in this plane. Let x, y and z denote the vectors obtained by drawing arrows from origin to P, Q and R. Determine conditions so that x, y and z be lineary dependent?
5. An infinite subset is lineary independent iff every finite subset of it is linearly independent!
6. If S and W are linearly independent sets what can one say about (the linear independence of) S È W , S Ç W and S \W and the symmetric difference S D W , defined as (S \W )È (W \S )?
7. S is linearly dependent iff 2S is linearly dependent. True or false?
8. The row vector of an m΄ n matrix A is the 1΄ mn matrix written in the partitioned form as vecR A = [A1 | A2 | ... | Am], where Aj denotes the j-th row of A. Similarly the column vector of A (written vec A Ί vecC A) is the mn΄ 1 matrix obtained by stacking the successive columns of A, the second below the first and so on. Verify that the maps A ® vecR A and A ® vecC A, are vector space isomorphisms of F m΄ n onto F 1΄ mn and F mn΄ 1, respectively. Deduce that a set S = {A : A Î S } is l.i. iff {vecR A : A Î S } is so, and similarly for the column case.
9. Show that two vectors are linearly dependent iff one of them is a scalar multiple of the other.
10. Find three vectors in F 3 which are linearly dependent, and are such that any two of them are linearly independent. Interpret such vectors as non-parallel vectors in a plane, when F = R .
11. Let V be a vector space over a field F . If a , b , g Î V are linearly independent, show that they span the same subspace as a +b , b +g , g +a iff ch (F ) Ή 2.
12. Let V be a vector space over a field F and let a , b , g Î V . Show that: (a) if ch (F ) Ή 2, the vectors a, b, g span the same subspace as a +b , b +g , g +a ; (b) if ch (F ) = 2, the vectors a , b , g span the same subspace as a +b , b +g , and g +a iff g lies in the span of a +g and b +g .
13. Let V be a vector space over a field F . Show that there are a finite number of vectors in V which span V iff no infinite subset of V is linearly independent.
14. Let A be an m΄ n matrix and let S = {v1, v2, ... ,vn}, where vj denotes the j-th column vector of A. Use Ax = x1v1 + x2v2 + ... + xnvn , to establish : (a) there is a non-zero x Î F n such that Ax = 0 iff S is linearly dependent; (b) Ax = b has at most one solution iff S is linearly independent; (c) Ax = b is consistent iff b Î <S >.
15. Prove that given any subset S of F n there exists an A Î F n΄ n such that the set of all solutions of Ax = 0 equals span {S }. Find one such A and give a description of all such As.
16. Let S Ì F n. Find the least m such that there is an m΄ n A such that span {S } equals the set of all solutions of Ax = 0.
17. Let A denote the matrix with the row vectors given as R1 = (1, 1, 1, 1), R2 = (0, 1, 0, 1), R3 = (1, 3, 1, 3), R4 = (2, 0, 2, 0). Construct a matrix B such that b = ABb , for all vectors b Î R (A), the range of A. Can you find such a B for any m΄ n A?
18. Prove that a system Ax = b of linear equations has a solution if and only if y’ b = 0, whenever y’ A = 0. (Duality criterion.)
19. Consider the usual three dimensional xyz-space with a point P in it with co-ordinates x, y, z, represented as (x,y,z) and the corresponding vector v represented as an arrow pointing from the origin to P as xi+yj+zk. Show that vectors v1 , v2 , v3 are linearly dependent iff the corresponding points P1, P2, P3 lie in a plane passing through the origin.
20. Which of the following statements are true? (i) {v1, ... , vm} is l.i. if one of vj s is 0. (ii) Any subset of a l.i. set is l.i. (iii) If v1, v2, v3 are l. d. vectors in R 3 there exists a plane passing through origin that contains them. (iv) The span of the set of all vectors x = (x1, x2) Î R 2 for which x2 = x12 is R 2 itself. (v) If S is a subset of a vector space V and <S > = S , then S is a subspace of V . (vi) A subspace of a vector space must always contain a non-zero element. (vii) If X and Y are subsets of a vector space V and X Ç Y = f , then <X >Ç <Y > = f .
21. If F Ì G are fields, and S a l.i. subset of F n, show that S is a l.i. subset of G n. Deduce that an n΄ n matrix A over F is non-singular iff it is non-singular over G .
3. Bases in a Vector Space
A set B in a vector space V is called a basis of V if (i) B is linearly independent, and (ii) any element in V can be written as a linear combination of elements of B .
Example. The vectors e1, e2, ... , en Î F n, defined by e1 = (1, 0, 0, ... , 0, 0, 0, ... , 0)’ , e2 = (0, 1, 0, ... , 0, 0, 0, , 0)’ , , ek = (0, 0, 0, , 0, 1, 0 , , 0)’ , , en = (0, 0, 0, , 0, 0, 0, , 1)’ , where the k-th component of ek is 1 and the rest are zero, are linearly independent and that x = x1e1 + x2e2 + + xnen, for any x = (x1, x2, , xn)’ Î F n. Hence, B = {e1, e2, , en} is a basis of F n. This basis is the standard for most computations cocerning F n and is called the standard basis of F n. The vectors eks are known as the standard unit vectors in F n.
Theorem. Let V be a vector space over a field F . If V Ή {0}, then V has a basis. If S is a l.i. set in V there exists a basis B of V containing S
Proof: Since V Ή {0}, and {v}, where v Ή 0, is l.i., the class of all l.i. subsets of V is non-empty and is partially ordered by inclusion. The union of any chain of such subsets is an upper bound for this chain. Hence by the Zorns lemma (the maximal principle), there exists a maximal l.i. subset in V , furnishing a basis. For proving the second assertion, we consider the class of l.i. subsets of V containing S and argue as in the case of the first assertion. #
PROBLEMS
1. Are the F 4-vectors (1, 2, 3, 4)’ , (4, 3, 2,1)’ , (1, 1, 1, 1)’ and (1, 0, 0, 1)’ linearly dependent? Find a basis for their span.
2. Show that a 1 = (1, 0, 1)’ , a 2 = (1, 2, 3)’ and a 3 = (3,2,1)’ form a basis for F iff F is not a field of characteristic 2. If F is not of characteristic 2, express each of the standard basis vectors in terms of a 1, a 2, and a 3.
3. Show that the set of all m΄ n matrices with one entry 1 and all the other entries 0 is a basis of F m΄ n.
4. Does the vector space F n΄ n possess a basis, each matrix A of which satisfies A2 = A? Begin with n = 2. The answer is "yes."
5. For a subset B of a vector space V , the following statements are equivalent: (a) B is a basis of V ; (b) B is a maximal l.i. subset of V . (c) B is l.i. and V = <B >.
6. Let V be the set of all infinite sequences {a1,a2, } over a field F in which all but a finite number of ai s are 0. With addition and scalar multiplication in V given by {a1, a2, ...}+{b1, b2, ...} = {a1+b1, a2+b2, } and c{a1, a2, } = {ca1, ca2, }, show that V is a vector space over F and find a basis of the same. What is the cardinality of this basis? Can you find a basis if the constraint "all but a finite number of ais are 0" is dropped?
4. Dimension of a Vector Space
A vector space V is called finite dimensional if every infinite subset of V is l.d. Conversely, if some infinite subset of V is l.i. V is called an infinite dimensional vector space. It follows that a basis in a finite dimensional vector space has only a finite number of elements in it. In fact the number of elements in a basis of a vector space is an invariant of the vector space:
Theorem. If m and n are two natural numbers and {u1, u2, ... ,um} and {v1,v2, ... ,vn} are two bases of a vector space V over a field F , then m = n.
Proof: If not, w.l.g. let m < n. The proof is by Steinitzs replacement argument. Since <u1, u2, ... ,um> = V ' v1, we can write v1 = S 1£ i£ m ciui, where at least one ci Ή 0 (as a set containing 0 can not be linearly independent). Renaming ui s, if necessary, w.l.g. we can assume that c1 Ή 0. Then, u1 = c1-1(v1 -S 2£ j£ m cjuj ) Î <v1, u2, ... ,um> and hence V = <v1, u2, ... ,um > ' v2 . Writing v2 = d1v1 + d2u2 + + dmum, where di Ή 0, for at least one i > 2 (else the linear independence of vi s is violated). Then u2 Î <v1, v2, ... ,um > = V ' v3, and so on. Continuing, in m steps we get < v1, v2, ... ,vm> = V ' vn . Hence the basis {v1,v2, ... ,vn} becomes a linearly dependent set, which is a contradiction. #
Alternate Proofs for the Equality of Number of Vectors in Bases:
Proof 1. Let {u1, u2, ... ,um} and {v1,v2, ... ,vn} be two l.i. sets spanning the same space. Via an isomorphism, w.l.g. the vectors could be regarded as column vectors. Consider the pooled matrix [U|V] whose columns are ui s and vj s. We first reduce it to its column echelon form by: (a) sweeping the columns of V through l.c.s of those of U and (b) by reducing U part. Since columns of U are l.i., the echelon form has precisely m non-zero columns. Another time we interchange U and V through ECOs and proceed w.r.t. V instead of U as before to get precisely n non-zero columns. Since the echelon form is unique it follows that m = n. #
Proof 2. Let [u1, u2, ... ,um] = [v1,v2, ... ,vn]A and [v1,v2, ... ,vn] = [u1, u2, ... ,um]B. Then A is n΄ m and B is m΄ n and [u1, u2, ... ,um] = [u1, u2, ... ,um]BA It follows that BA = I . Similarly AB = I . However, these are impossible in the respective cases m > n and n > m. So m = n. #
Corollary. Elementary operations on a set S of vectors do not change the maximum number of linearly independent elements in S .
Proof: Any set of maximum number of l.i. elements forms a basis of the space spanned by all the vectors. Hence this number is invariant by the previous result. #
In view of the theorem above, any two bases in a finite dimensional vector space have the same number of elements. This common number of elements is called the dimension of the vector space.
Corollary. If V is an n-dimensional vector space, a subset of V having more than n elements is linearly dependent and a subset consisting of n linearly independent elements is a basis of V .
Proof: Since any l.i. subset can be extended to a basis, the results are clear in view of the above theorem. #
A basis of a vector space in which the elements have been ordered in some fashion is called an ordered basis. For an ordered basis we then can talk about the first, the second etc. elements. One of the most important uses of an ordered basis is to introduce the notion of coordinates of a vector, using which many problems could be solved by easy computations. The ordered basis B = {e1, e2, ... ,en}, of F n where ejs are the standard unit vectors (1, 0, ), (0, 1, 0, ) etc., is called the standard ordered basis of F n.
If B = {v1,v2, ... ,vn} is an ordered basis of a n-dimensional vector space V , and if v is an element of V , for some scalars xjs we can write v = x1v1 + x2v2 + + xnvn.
The representation of v as a l.c. of vjs is unique due to the l.i. of vjs. Symbolically, treating B = {v1,v2, ,vn} as a row vector whose entries themselves are vectors and interpreting vc as cv, if v is a vector and c is a scalar we can rewrite the above as v = B x, where x denotes the column vector (x1, x2, , xn)’ and is known as the coordinate vector, or the matrix of v with respect to the ordered basis B of V . We write x = [v]B and then we have v = B [v]B .
The map v ® x = [v]B is a one to one onto correspondence between the elements of V and F n, which preserves addition and scalar multiplication, [au + bw]B = a[u]B + b[w]B , i.e., it is a vector space isomorphism :
Theorem. Let V be an n-dimensional vector space over a field F . Then V is isomorphic to F n.
As a corollary, a linear relation in vs holds iff it holds in the corresponding xs, and as a consequence a subset S of V is linearly dependent iff the subset S B = {[v]B : v Î S } is linearly dependent in F n. This fact and a right choice of a basis B is the key to a great many computations one comes across in practice.
PROBLEMS
1. Consider the vector space F 3΄ 3. Let W 1 be the set of matrices of the form
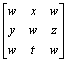 ,
,
and W 2 that of matrices of the form
 .
.
Check that W 1 and W 2 are subspaces of F 3΄ 3 and find the dimensions of the subspaces W 1, W 2, W 1 Ç W 2 and W 1 + W 2.
2. What is the dimension of the vector space R over the field Q of rational numbers? What is the answer in the case of C over R ? What is the dimension of F m΄ n as a vector space over F .
3. Show that the following sets of n΄ n complex matrices, with the usual operations, are vector spaces over R and find the dimension of the same: (a) matrices of trace zero; (b) matrices A such that A* A = 0; (c) matrices such that A* = A; matrices such that A* = -A. Which of these are vector spaces over C ?
4. Regard R as a vector space over the field Q of rational numbers, with the usual operations. Is it true that this vector space has a countable basis?
5. Show that the vectors a1 = (1, 1, 1, 1), a2 = (0, 1, 1, 1), a3 = (0, 0, 1, 1), a4 = (0, 0, 0, 1), form a basis for row-space R(4). Find the coordinates of each of the standard basis vectors in the ordered basis {a1, a2, a3, a4}.
6. Find the coordinate matrix of the vector (0, 1, 0) in the basis of C(3) consisting of the vectors (1-i, 0, 1+i), (1+i, 1-i, 0), (0, 1+i, 1-i), in that order.
7. If w Ή 1 is a cube root of 1, prove that B 1 = {(1, w , w 2), (w 2, w , 1)} and B 2 = {(2, -1, -1), (-1, -1, 2)} are ordered bases of the subspace W 0 of the space C (3) spanned by the row vectors (1, 0, -1), (-1, 1, 0), (0, -1, 1). Find the coordinates of (-1, 2, -1) in these bases?
8. Let a = (x1, x2)’ and b = (y1, y2)’ be vectors in R 2 such that x1y1 + x2y2 = 0, x12 + x22 = y12 + y22 = 1. Prove that B = {a , b } is a basis for C 2 and find the coordinates of a vector (a, b)’ in the ordered basis B . If a , b satisfy the above equations but belong to C 2, give an example to show that {a , b } need not form a basis of C 2.
9. Let V be the vector space over C of all comples-valued functions on the real line. Prove that B = {ei(j-n-1)x}1£ j<₯ is a linearly independent set in V and that it spans the subspace T n of all complex trigonometric polynomials of order £ n. Find [B ]T , the matrix of B with respect to the ordered basis T = {1, cos x, sin x, ... , cos nx, sin nx} of T n.
10. Let P n-1 be the (real) vector space of all polynomials functions from R into R of degree less than n. Let a be a fixed real number and define g1(x) = 1, g2(x) = x-a, ... , gn(x) = (x-a)n-1. Prove that B = {g1, g2, , gn} is a basis for P n and that the coordinate vector of an f Î P n-1 in the basis B is given by [f] = (f(a), f’ (a), f’ ’ (a)/2!, , f(n-1)(a)/(n-1)!)’ .
11. Construct an isomorphism of the vector space C n over the field R onto the vector space R 2n over R .
12. Let V be a vector space over a field F isomorphic to the vector space F 2 . Let a 1, a 2, a 3 Î V be such that Ta 1 = (1, 0), Ta 2 = (-1, 0), Ta 3 = (-1, 1). (a) Check if a 1 belongs to <a 2, a 3>? (b) Find <a 1, a 2> Ç <a 2, a 3>. (c) Find a basis for <a 1, a 2, a 3>.
13. Let S be a set of non-zero polynomials over a field F . Show that: (a) if no two elements of S have the same degree, S is an independent set in F [x]; (b) if S is an independent set and if each polynomial in S is of degree n, S has at most n+1 elements; (c) if S is independent and h is a non-zero polynomial, S = {ph : p Î S } is independent.
14. Find conditions on a, b Î F so that the polynomials 1, ax+b, (ax+b)2 , (ax+b)3, form a basis of F [x].
15. Prove that finite-dimensional vector spaces over a field are isomorphic iff they have the same dimension.
16. Let V and W be vector spaces over a field F and let S Î L(V , W ) be invertible. Prove that T ® S-1TS is an isomorphism of L(W , W ) onto L(V , V ).
17. Verify that h : (x, y, z, t)’ ® ![]() ,
,
is an isomorphism of R 4 onto the subspace H 2 of C 2΄ 2 over R , of all 2x2 complex Hermitian matrices. Derive an isomorphism h 0 : R 3 ® H 20 , the subspace of H 2 of matrices of trace zero with det h 0(x) = ||x||2.
18. Show that F m΄ n is isomorphic to F n΄ m.
19. If xi Î F , 0 £ i £ n are distinct, prove that the polynomials lk(x) = P jΉ k, 0 £ j £ n [(x-xj)/(xk-xj)], 0 £ k £ n, form a basis of the vector space of all polynomials of degree £ n. Find the coordinates of a polynomial P(x) = c0 + c1x + ... + cnxn with respect to the ordered asis B = {l0, l1, ... , ln}.
20. If a, b, c, d Î F are distinct, prove that a quadratic P, satisfying P(a) = a , P(b) = b , P(c) = g and P(d) = d , where a , b , g , d Î F , exists iff
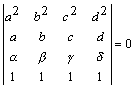 .
.
5. Direct Sum Decomposition of a Vector Space
A sum
W = W 1 + W 2 + ... + W k of subspaces W is is called a direct sum if each w Î W has a unique representation w = w1 + w2 + ... + wk, (wi Î Wi ). The statement that the sum W1 + W 2 + ... + W k is a direct sum, is equivalent to the assertion that w1 + w2 + ... + wk = 0, (wi Î W i), iff wi = 0, 1 £ i £ k. If this assertion holds, we say that the subspaces W i are linearly independent or simply independent.To distinguish a direct sum from an ordinary sum, we circle the sum symbol and write it as
W
= W 1 Å W 2 Å Å W k.If
V i, 1 £ i £ m, are independent subspaces of a vector space V and V = V 1 Å V 2 Å Å V m, the direct sum V 1 Å V 2 Å Å V m is called a direct sum decomposition of the vector space V . Using the notion of a direct sum decompositon, many problems concerning a large vector space V could possibly be reduced to another set of relatively easier problems over the smaller vector spaces V is.PROBLEMS
1
. Let R 1, R 2 , , R n denote the one dimensional subspaces of R n, generated by the standard unit vectors e1, e2 , , en. Are the subspaces R i independent? If so, is R n = R 1 Å R 2 Å Å R n?2. If
W is a subspace of V and V = V 1 Å V 2 Å Å V m, is it true that W = (W Ç V 1 ) Å (W Ç V 2 ) Å Å (W Ç V m)?3. Prove that
V 1 + V 2 + + V m is a direct sum iff dim (V 1 + V 2 + + V m) = dim V 1 + dim V 2 + + dim V m.4. Prove that two subspaces
W 1 and W 2 are linearly independent iff W 1 Ç W 2 = {0}. What would be a orresponding generalization in the case of k subspaces W 1, W 2, ... , W k?5. If
V = V 1 Å V 2 Å Å V m, verify that: (a) dim V = S 1£ i£ m dim V i; (b) If B i = {vi1, vi2, , vin(i)} is an ordered basis of the subspace V i , 1 £ i £ m, the pooled ordered set B = {B 1, , B m} Ί {v11 , , v1n(1) , , vm1, ... , vmn(m)} is an ordered basis of V .6. If
V is a vector space and W 1 any subspace of V , show that there exists a subspace W 2 of V such that V = W 1 Å W 2. When will W 2 be unique.7. If
V is a finite-dimensional vector space and W 1, W 2, ... , W k are subspaces of V such that V = W 1 + + W k, show that dim V £ dim W 1 + + dim W k, the equality holding iff V = W 1 Å Å W k.8. Find conditions for the existence of an operator P that projects a vector space
V onto a given subspace W along a given subspace W 0, and determine P explicitly in the following cases: (a) V = F (2) , W = span {(1, 0)} and W 0 = span {(0, 1)}; (b) V = F (2) , W = span {(1,2)} and W 0 = span {(2,1)}; (c) V = F (2) , W = span {(a, b)} and W 0 = span {(c, d)}; (d) V = F n , W = the span of the first k columns of an n΄ n matrix A and W 0 = the span of the remaining columns of A.9. Let Q(x) = a0xn + a1xn-1 + ... + an-1x + an be a polynomial and P
Ή I be a projection operator. Find conditions so that Q(P) be invertible.10. Which of the following statements are true? (a) If Ei, 1
£ i £ k are projections onto linearly independent subspaces W i , their sum E1 + E2 + + Ek is also a projection. (b) If E is a projection and a Ή 0, then aI + bE is a projection iff a = 1 and b = -1. (c) A diagonalizable operator is a projection iff its eigenvalues are only 0 and 1. (d) If E2 is the projection on W along W 0 , then (I-E) is the projection on W 0 along W . (e) If E1, , Ek are projections and E1 + + Ek = I, then EiEj = 0 for i Ή j. (f) If E1 , , Ek are linear operators, E1 + + Ek = I, and EiEj = 0 for i Ή j, then Eis are projections.11. If P (
Ή 0, I) is a projection and a and b are non-zero scalars prove that aI + bP is invertible iff a Ή -b, and that (aI + bP) = a-1I - (a + b)-1a-1bP.12. Let
F be a field characteristic zero (e. g., R , or C ). Let V be a finite-dimensional vector space over F . If E1, , Ek are projections of V and E1 + ... + Ek = I, prove that EiEj = 0 for i Ή j. (Hint : Use the trace function and ask yourself what the trace of a projection is).13. Let
V be a vector space, let W 1, ,W k be subspaces of V , and let V j = W 1 + + W j-1 + W j+1 + + W k. If V = W 1 Å Å W k, show that the dual space V * has the direct sum decomposition V * = V 10 Å Å V k0.