8

Jordan Canonical Form

The characteristic polynomial f_T(x) of a linear operator T on a vector space V of dimension n may, unambigously, be defined as the characteristic polynomial f_[T](x) of the matrix [T] of T with respect to any basis b of V . This is because, in view of the relation [T]b = [b ]a ^-1[T]a [b ]a for any two bases a and b , all such matrices are similar and so have the same characteristic polynomial.

If W is a subspace of V such that Tw Î W for all w Î W , W is said to be T-invariant. For such a W , the restriction R of T to W is a linear operator on W . If a basis w = {w₁, w₂, … , w_m} of W is extended to an ordered basis b = {w₁, w₂, … , w_m, v_m+1, … , v_n} of V , there follows

[T] = ,

for some m´ (n-m) matrix X and (n-m)´ (n-m) Y. It follows that f_T(x) = f_R(x)f_Y(x), showing that the characteristic polynomial of a restriction of T divides the characteristic polynomial of T. In particular, if f_T(x) is a product of linear factors so is f_R(x).

If (l , v) is an eigenpair of T (i.e., v ¹ 0, and Tv = l v), W = <v>, the span of v, is T-invariant and the characteristic polynomial of the restriction of T to <v> is simply (x-l ). It follows that (x-l ) divides f_T(x). Conversely, if (x-l ) is a factor of f_T(x), l I-T is singular and so there exists a vector v such that (l , v) is an eigenpair of T. The above background is enough to prove the important:

Jordan Canonical Form Theorem. If T is a linear operator on a finite dimensional vector space V over a field F such that f_T(x) is a product of linear factors, there exists a basis b of V such that [T]b is of a Jordan canonical form.

Proof: Let dim(V ) = n. Let the characteristic polynomial f_t(x) of T be a product of linear factors. Let l be an eigenvalue of T. Put S = T - l I. Then S is singular and dim (S(V )) < n. By an induction on the dimension of the vector space, we can assume that to S restricted to S(V ) there corresponds a Jordan basis

g = {z_i,j: 1 £ j £ l(i), 1 £ i £ p}È {y_i,j: 1 £ j £ m(i), 1 £ i £ q},

where z_i,j 's are associated with blocks of zero eigenvalues and y_i,j 's with the non-zero eigenvalues l _i 's:

Sz_i,1 = 0, Sz_i,j = z_i,j-1, 1 < j £ l(i) , 1 £ i £ p,

Sy_i,1 = l y_i,1, Sy_i,j = l _iy_i,j + y_i,j-1, 1 < j £ m(i), 1 £ i £ q.

Since z_i,l(i) Î S(V ), there exist z_i Î V such that

Sz_i = z_i,l(i), 1 £ i £ p.

Let {z_i,1: 1 £ i £ p}È {x_i: 1 £ i £ r} be a basis of null space N (S) of S. We show that the following ordered set b is a Jordan basis for T in V :

b = {{z_i,1, z_i,2, … , z_i,l(i), z_i: 1 £ i £ p}È {y_i,j: 1 £ j £ m(i), 1 £ i £ q}È {x_i: 1 £ i £ r}}.

To show that the set b is linearly independent, let

0 = S ₁£ i£ p (S ₁£ j£ l(i) a_i,j z_i,j + a_i z_i) + S ₁£ i£ q (S ₁£ j£ m(i) b_i,j y_i,j +S ₁£ i£ r c_i x_i.

Operating by S, we have

0 = S ₁£ i£ p (S ₂£ j£ l(i) a_i,j z_i,j-1 + a_i z_i,l(i)) + S ₁£ i£ q [S ₂£ j£ m(i) b_i,j (l _iy_i,j +y_i,j-1) + b_i1 l _i y_i,1].

By the linear independence of z_i,j 's and y_i,j 's we have

a_ij = 0, 2 £ j £ l(i) , 1 £ i £ p; a_i = 0, 1 £ i £ p; b_ij = 0, 2 £ j £ m(i) , 1 £ i £ q; b_i1 = 0, 1 £ i £ q.

Using these, for the remaining coefficients, we have

S ₁£ i£ p a_i1 z_i,1 + S ₁£ i£ r c_i x_i = 0,

which by the linear independence of z_i,1 's and x_i 's implies a_i1 = 0, 1 £ i £ p; c_i = 0, 1 £ i £ r, establishing that b is a linearly independent set. Note that the number of vectors z_i,j 's and y_i,j 's equals the rank of S, and the number of vectors z_i 's and x_i 's equals the nullity of S. Hence b is a basis of V . Clearly b is a Jordan basis for S and hence for T. #

The above matrix [T]b itself is generally referred to as a Jordan canonical form of T.

Corollary. Let l be an eigenvalue of T and root of a polynomial P(x) of order m. Then, in the Jordan canonical form of T, if l is associated with l Jordan blocks of sizes {m_i´ m_i: 1 £ i £ l}, the Jordan blocks in the Jordan canonical form of the operator P(T), corresponding to its eigenvalue P(l ) have the sizes {(m_i-m)´ (m_i-m): m_i > m} their number equalling the number of m_i 's larger than m. If l is not a root of P(x), in the Jordan canonical form of P(T), P(l ) is associated with the same number of Jordan blocks and of the same sizes as is l in the Jordan canonical form of T.

PROBLEMS

1. Prove that to a linear operator T on a vector space V there corresponds a Jordan basis iff to T there corresponds a triangulizing basis.

2. Show that the number of linearly independent eigenvectors possessed by a triangulable operator equals the number of Jordan blocks in its Jordan canonical form.

3. Prove that a Jordan canonical form of an operator is unique except for a reordering of its Jordan blocks.

4. If A is a triangulable matrix, show that there exists a non-singular matrix C such that C^-1AC is in Jordan canonical form.

Rank of a Linear Transformation

The rank of a linear transformation T : U ® V , denoted by r(T) is defined to be the dimension of its range space R (T) = {Tu : u Î U }. The null space N (T) = {u Î U : Tu = 0}, of T is the subspace of vectors u annihilated by T. The dimension of N (T) is called the nullity of T and is written as n(T).

Example. If V is the vector space of all 2´ 2 matrices over a field F and T Î L(V ) is defined by

then, if F is not of characteristic 2,

N (T) = {: x Î F } , R (T) = {: x, y, z Î F }

and if ch (F ) = 2, then

N (T) = {: x, z Î F } , R (T) = {: y, z Î F }.

Theorem. Let T : V ® W be a linear transformation. Then r(T) + n(T) = dim V .

Proof: Let {v₁, … , v_n} be a basis of R (T). There exist u₁, … , u_r Î V such that Tu_i = v_i , i = 1, ... , r. Let {w₁, … , w_k} be a basis of N (T). Let U = span {u₁, … , u_r}. Let x Î V . Write Tx = S a_iv_i . Then x - S a_iu_i Î N (T). Write x - S a_iu_i = S b_jw_j . Then x = S a_iu_i + S b_jw_j Î span {u₁, … , u_r, w₁, … , w_k} = V (therefore). It remains to show that {u₁, … , u_r, w₁, … , w_k} is an independent set. If not, there exist non-trivial scalars p_i, q_j 's such that S p_iu_i + S q_jw_j = 0. All p_i 's can't be zero, for otherwise independence of w_j 's is contradicted. Now 0 = T(S p_iu_i + S q_jw_j) = S p_iv_i , contradicting independence of v_i 's. #

PROBLEMS

1. Let T be a linear operator on a two dimensional vector space V . If T² = T prove that T = 0 or T = I or that there is a basis b of V such that

[T]b = .

2. Let T be a linear operator on a two dimensional vector space V . If r(T) = 2 and T² = T, prove that T = I.

3. Let T be a linear operator on a two dimensional complex or real vector space. Let lim_n® ¥ Tⁿ = T (in the sense that the entries in the matrix of Tⁿ approach the corresponding entries in the matrix of T with respect to some basis). Prove that T = 0, I, or that for some basis b ,

[T]b = .

4. Let T be a linear operator on a two dimensional complex or real vector space. Let lim_n® ¥ Tⁿ = S. Prove that S = 0, I, or, that for some basis b ,

[S]b = .

.5. Let B be n´ p and A an m´ n matrix over a field F . Prove that R (A¢ ) = N (B¢ ) iff R (B) = N (A).

Linear Functionals

A linear functional f on a vector space V is simply a linear transformation from V to F. The set of all linear functionals on V is denoted by V ¢ and is called the algebraic dual of V . Thus, V ¢ = L(V , F), is a vector space, with the usual operations, and V ¢ is isomorphic to V if V is finite dimensional. The dual space V ¢ of V deserves a special consideration due to its role in analysing problems on V .

If {va : a Î J} = b is a basis of V , J being an indexing set, and j : J ® F is any map, the rule f (va ) = j (a ), determines the most general linear functional f for which, writing v = S a Î _J ca va , v Î V , where all but a finite number of ca 's are zero on the right so that the sum is actually finite for each v Î V , we have f (v) = S a Î _J ca f (va ) = S a Î _J ca j (va ). If J is finite, for a given basis b = {va : a Î J} of V , the linear functionals f a determined by f a (vw ) = d a w , a , w Î J, are linearly independent, and any linear functional f on V can be written as the linear combination f = S a Î _J f (va )f a . In particular, if V = F ⁿ, f is a linear functional on V , and e_i is the i-th standard unit vector in F ⁿ, putting y_i = f (e_i), 1 £ i £ n, f(x) = S ₁£ i£ n f (e_i)x_i = S ₁£ i£ n y_ix_i = y¢ x, and the correspondence f « y Î F ⁿ is obviously 1-1 onto.

Lemma. f ₁, f ₂, … , f _m Î V ¢ are ll.i. iff there exist vectors u₁, u₂, … , u_m Î V , such that det (f _i (v_j)) ¹ 0.

Proof: If f _i 's are linearly dependent one of them is a linear combination of the others and then the corresponding row of (f _i(u_j)) is a linear combination of the other rows and so det (f _i(u_j)) = 0. This proves the 'if' part. For the 'only if' part, we note that if m = 1 the result is true. For, {f ₁} l.i. is equivalent to f ₁ ¹ 0, in which case there exists a w₁ such that f ₁(w₁) ¹ 0. Thus assume the result for m and let f ₁, f ₂, … , f _m, f _m+1 be l.i. Then ff ₁, f ₂, … , f _m are l.i. and so there exist u₁, … , u_m s.t. det (f _i(u_j))₁£ i,j£ m ¹ 0. Let u be an arbitrary vector and consider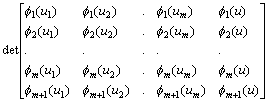

Suppose for no u is it different from zero. Let C₁, C₂, … , C_m+1 denote the cofactors corresponding to the elements in the last column. Then for all u, 0 = S ₁£ i£ m+1 C_if i(u) implies that S ₁£ i£ m+1 C_if i = 0. By linear independence of f _i 's, C_m+1 = 0. But C_m+1 = det (f _i (u_j)₁£ i,j£ m) ¹ 0, a contradiction. This completes the proof. #

Lemma. f ₁, f ₂, … , f _m Î V ¢ are l.i. iff there exist v₁, v₂, … , v_m Î V , such that f _i(v_j) = d _ij, i, j = 1, 2, … , m.

Proof: If f _i(v_j) = d _ij, det (f _i(v_j)) = 1 ¹ 0. By the previous lemma f ₁, f ₂, … , f _m are linearly independent. Conversely, if f ₁, f ₂, … , f _m are l.i., by the previous lemma there exist vectors u₁, … , u_m s.t. det (f _i(u_j)) ¹ 0. Then for each 1 £ k £ m, the system S ₁£ j£ m a_kj f _i(u_j) = d _ki , i = 1, … , m, has a solution. Hence, putting v_k = S ₁£ j£ m a_kju_j, we have f _i(v_k) = d _ik , i,k = 1, ... , m. #

Theorem. T Î L(V , W ) has rank m iff there exist l.i. f ₁, f ₂, … , f _m Î V ¢ and l.i. w₁, … , w_m Î W , such that T = S ₁£ i£ m f _i w_i, i.e., Tv = S ₁£ i£ m f _i(v)w_i, v Î V .

Proof. If T is of the given form R (T) Ì span {w₁, … , w_m}. By the previous lemma, T(v_j) = S ₁£ i<m f _i(v_j) w_i = S ₁£ i<m d _ij w_i = w_j, and hence, w_j Î R (T), j = 1, … , m. As w_j 's are linearly independent, dim R (T) = dim (span {w₁, … ,w_m}) = m. Conversely, let r(T) = m, and let w₁, … , w_m span R (T). Then for some functionals f _i, i = 1, ... , m, Tu = S ₁£ i£ m f _i(u)w_i. Thus, S ₁£ i£ m f _i(au+bv)w_i = T(au+bv) = aTu + bTv = S ₁£ i£ m af _i(u)+bf _i(v)w_i. The linear independence of w_i 's implies that f _i(au + bv) = af _i(u) + bf _i(v) for i = 1, ... , m and for all vectors u, v and scalars a, b. Thus each f _i is a linear functional. If f _i 's are not l.i., w.l.g. let f _m = S ₁£ i£ m-1 a_i f _i. Then, Tu = S ₁£ i£ m f _i(u)w_i = S ₁£ i£ m-1 f _i(u)(w_i + a_iw_m), implying that r(T) £ m-1, a contradiction. Thus f _i 's and w_i 's are l.i., completing the proof. #

Corollary. Let A be an m´ n matrix. Then r(A) = r iff there exist r l.i. m´ 1 vectors w₁, w₂, … , w_r and r l.i. n´ 1 vectors u₁, u₂, … , u_r such that

A = S ₁£ i£ r u_i w_i¢ = .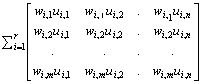

Corollary. Let f , f ₁, f ₂, … , f _k Î V ¢ and N (f ), N (f ₁), ... , N (f _k) denote their null spaces. Then f is a linear combination of f ₁, f ₂, … , f _k iff Ç ₁£ i£ k N (f _i) Ì N (f ).

Proof: Without loss of generality, we can assume that f ₁, f ₂, … , f _m are l.i., m £ k, and that f _i, i > m can be written as l.c.'s of f ₁, f ₂, … , f _m. Now N _k = Ç ₁£ i£ k N (f _i)Ì Ç ₁£ i£ m N(f _i) = N _m. Also if j > m and v Î N _m then f _j(v) = 0 implies v Î N (f _j). Hence N _m Ì N (f _j), j ³ m+1. It follows that N _k = N _m. Hence, it is sufficient to prove that f is a l.c. of f ₁, f ₂, … , f _m iff N _m Ì N (f ), where f ₁, f ₂, … , f _m are l.i.

Now, if f is an l.c. of f _i 's, obviously Ç N (f _i) Ì N (f ). And if f is not an l.c. of f _i 's, f , f ₁, f ₂, … , f _mare l.i. as f _i 's are so. But by the theorem, then, there is a v s.t. f (v) = 1 and f _i(v) = 0 and so Ç N (f _i) is not contained in N (f ). #

PROBLEMS

1. In R ³ , let u₁ = (2, 1, 1)¢ , u₂ = (1, 2, 1)¢ , u₃ = (1, 1, 2)¢ . (A) If f is a linear functional on R ³ such that f(u₁) = 1, f(u₂) = 2, f(u₃) = 3, and if u = (1, 2, 3)¢ , find f(u). (B) Describe explicitly a linear functional f on R ³ such that f(u₁ + u₂ ) = f(u₂ + u₃ ) = 0 but f(u₁ + u₃) ¹ 0. (C) Let f be any linear functional such that f(u₁ + u₂ ) = f(u₂ + u₃ ) = 0, and, f(u₁ + u₃) ¹ 0. If u = (1, 1, 1), show that f(u) ¹ 0.

2. Let u₁ = (1, 1, 1)¢ , u₂ = (1, w , w ²)¢ , and u₃= (1, w ², w )¢ , where w ¹ 1 is a cube root of 1. Is b = {u₁, u₂, u₃} a basis for C ³? If so, find the dual basis of b . What is the matrix of the identity operator relative to b ?

3. Let V be a finite dimensional vector space, b = {u₁, … , u_n} a basis of V and w = {f₁, … , f_n} the dual basis. If T Î L(V ), we define the trace of T by tr T = S ₁£ i£ n f_i (Tu_i). Show that : (a) the trace function is independent of the choice of the basis b ; (b) tr TS = tr ST; and (c) tr T = tr [T]b , for any basi b of V , where the trace of a matrix is the familiar sum of its diagonal entries.

4. Let V be the vector space of all real polynomial functions p(x) = c₀+c₁x+…+c_n-1x^n-1 on R of degree < n. Define the linear functionals f_k 's on V by: f_k(x) = ò _[0,k] p(x) dx, 1 £ k £ n. Show that {f₁, f₂, … , f_n} is a basis for V ¢ . Exhibit the basis for V of which it is the dual.

5. If T and S are linear operators on a finite dimensional vector space over a field of characteristic zero, show that the relation TS - ST = I is impossible.

6. Show that every T Î L(F ⁿ, F ^m) can be expressed as Tx = (f₁(x), … , f_m(x))¢ , x Î F ⁿ, for some linear functionals f₁, … , f_n on F ⁿ, uniquely determined by T. Use this result to show that N (T) can be written as an intersection of m subspaces of F ⁿ, each of dimension n-1. What are the f₁, f₂, … , f_m if n = m and T = I on F ⁿ.

7. If u₁ = (1, 1, 1, 1), u₂ = (1, 2, 3, 4), u₃ = (4, 3, 2, 1), and if W is the span of u₁, u₂ and u₃ in the row space C ⁽⁴⁾, characterize the linear functionals f: f(x) = y¢x lying in the annihilator of W ⁰, by finding a basis of W ⁰.

8. Find a basis for W ⁰, if W denotes the subspace of R ⁵ spanned by the three vectors u₁ = e₁+e₂+e₃, u₂ = e₂+e₃+e₄, u₃= e₃+e₄+e₅.

9. Let P denote the 2´ 2 real symmetric matrix such that P² = P and (1, 1)¢ Px = 0, x Î R ². Let W consist of matrices A Î R ²´ 2 such that AP = 0. Are there f Î W ⁰ such that f(B) = 0, and f(C) = 1, if

B = and C = ?

10. If the linear functionals f_k on R ⁿ are defined by f_k(x₁, … , x_n) = S ₁£ j£ n (k²–j²)x_j, 1 £ k £ n, find the dimension of the subspace annihilated by f₁, … , f_n.

11. If W ₁ and W ₂ are subspaces of F ⁿ, prove that : (a) (W ₁+W ₂)⁰ = W ₁⁰ Ç W ₂⁰ ; (b) (W ₁ Ç W ₂)⁰ = W ₁⁰+W ₂⁰.

12. If f is any non-zero linear functional on the vector space F [x] of polynomials over a field F such that f (fg) = f (f)f (g), for all f, g Î F [x], show that for some c Î F , f (f) = f(c), f Î F [x].

13. Let V be a vector space over a field F and let W be a subspace of V . If f is a linear functional on W , show that it can be extended as a linear functional on the whole of V , i.e., there is a linear functional g on V such that g(w) = f(w), w Î W . Find the dimension of the subspace of all such functionals g if V is finite dimensional.

14. Let F be a field having at least three distinct elements. Let V be any vector space over F . If f and g are linear functionals on V such that the function h defined by h(v) = f(v)g(v) is also a linear functional on V , prove that either f = 0, or g = 0. If F has no more than two elements, verify that the conclusion is false.

15. Let F be any infinite field and let V be a finite-dimensional vector space over F . If v₁ , ... , v_m are finitely many non-zero vectors in V , prove that there is a linear functional f on V such that f(v_i) ¹ 0, 1 £ i £ m.

16. If W is an n-dimensional vector space over a field F , the dual space W ¢ , being isomorphic to W , could be 'naturally' identified with W itself. In particular, if W = F ⁽ⁿ⁾, f Î W ¢ iff f has the form : f(x₁, x₂, … , x_n) = w₁x₁ + w₂x₂ + … + w_nx_n, where (w₁, w₂, … , w_n) Î W , itself. Now let n be a positive integer and F a field. Let W be the set of row vectors (x₁, x₂, … , x_n) in F ⁽ⁿ⁾ such that x₁ + x₂ + … + x_n = 0. Is it true that W ¢ consists of linear functionals f(x₁, x₂, … , x_n) = c₁x₁ + c₂x₂ + … + c_nx_n, on F ⁽ⁿ⁾ which satisfy c₁ + c₂ + … + c_n = 0? Verify that this happens iff the characteristic of the field ch (F ) Œ n.

17. Let z Î V = F ⁿ and let W = {x Î F ⁿ : z¢x = 0}. Let g Î V ¢ be defined by g(x) = z¢x, x Î V . Show that: (a) W is precisely the one dimensional subspace spanned by the linear functional g; (b) W ¢ can be 'naturally' identified with the restriction to W of all linear functionals f on V of the form f(x) = w¢ x, where w Î W , iff w¢ w ¹ 0; and, (c) if w¢ w = 0, then W ¢ can be identified with the restriction to W of all f Î V ¢ of the form f(x) = u¢ x, u Î U , where U is any subspace of F ⁿ such that F ⁿ = <w>Å U .

18. Characterize subspaces W of an infinite dimensional vector space V such that W is finite dimensional.

19. If W is a finite dimensional subspace of a vector space V , show that W ⁰ = {f Î V ¢: f(w) = 0, w Î W } is finite dimensional iff V is finite dimensional.

20. If W is a subspace of finite dimensional vector space V , and {f₁, … , f_r} Ì V ¢ is any basis for W ⁰, show that W = Ç ₁£ i£ r N (f_i) .

21. Let V denote the vector space of all functions from a given set S into a field F with the usual operations. Show that for any n-dimensional subspace W of V , there exist points x₁, … , x_n Î S , and functions f₁, … , f_n Î W such that f_i(x_j) = d _ij, 1 £ i, j £ n.

22. Let V and W be respectively, n and m-dimensional vector spaces over a field F . If R Î L(V ), S Î L(W ) and T is a linear operator defined on L(V , W ) by T(U) = SUR, prove that tr(T) = mn´ tr(S)´ tr(R).

23. Let V be a finite dimensional vector space over a field F . If f is a linear functional on L(V ) such that f(TS) = f(ST), for all S, T Î L(V ) show that f is a scalar multiple of the trace function on L(V ). If, in addition, f(I) = n, and if the characteristic of the field F does not divide n, then f is the trace function.

24. If V is a finite dimensional vector space, any operators T on V of the form T = RS-SR, S, R Î L(V ), is of trace zero. Show that there are enough operators of this type so as to span the subspace of all linear operators on V of trace zero.

25. If V is a vector space show that each v Î V defines a linear functional f _v on V ¢ by f _v(f) = f(v), f Î V ¢ and that (V ¢ )¢ is 'naturally' isomorphic to the subspace {f _v: v Î V } of (V ¢ )¢ under the correspondence v « f _v.

26. Prove that V ¢ is isomorphic to V iff dim V < ¥ .

The Transpose of a Linear Transformation

The transpose of a linear tranformation T e L(V , W ) is a transformation in L(W ¢, V ¢), written T^t or T¢ , defined by (T¢ f)(v) = f(Tv), f e W ¢, v e V , in which the right hand side is linear in f, T, as well as v, so that T¢ is unabigously defined and moreover we have (aT + bS)¢ = aT¢ + bS¢ , a, b e F, T, S e L(V , W ), showing that the operation of taking the transpose is a linear operation from L(V , W ) to L(W ¢, V ¢). If we agree to write g(v) as (v, g), the relation between T and T¢ could be expressed simply as (Tv, g) = (v, T¢ g), g e W ¢ , v e V .

The dual space V ¢ ¢ of the dual space V ¢ of V is called the bi-dual or the double dual of V . The map i : v ® F _v e V ¢ ¢ , v e V , defined by F _v(f ) = f (v), f e V ¢, is a homomorphism of V into V ¢¢ (a linear transformation from V to V ¢¢), the homomorphic image of V under i being R (i), the range of i. Since f (v) = 0, f e V ¢ , implies that v = 0, i is an isomorhism of V into V ¢ ¢ (i.e., i is invertible as a transformation from V to R (i) Ì V ¢ ¢ ). If V is finite dimensional dim V = dim V ¢ = dim V ¢ ¢ = dim R (i), so that R (i) = V ¢ ¢ and i is an isomorphism between V and V ¢ ¢ (an isomorphism of V onto V ¢ ¢ ).

Hence, in case V and W are finite dimensional vector spaces, V ¢ ¢ and W ¢ ¢ can be identified, respectively, with V and W in the sense that any F e V ¢ ¢ is, for some v e V , of the form F _v given by F _v(f ) = f (v), f e V ¢ , and, similarly, any Y e W ¢ ¢ is a Y g , for a g in W , given by Y g (y ) = y (g ), y e W ¢ . With these identifications, the transpose of the transpose of T, T¢¢ : V ® W is given by y (T¢ ¢ v) = (T¢ y )v = y (Tv), y e W ¢ , v e V . Since this relation holds for all y e W ¢ , T¢ ¢ v = Tv, v e V , which in turn, as v e V is arbitrary, implies that T¢ ¢ = T. Hence, T¢ ¢ for a linear transformation T from a finite dimensional vector spaces V to another finite dimensional vector space W gets identified with the transformation T itself.

Taking V = Fⁿ and W = F^m and identifying L(Fⁿ, F^m) with the space F^{m´ n} of the m´ n matrix transformation, (Fⁿ)¢ with F⁽ⁿ⁾ and (F^m)¢ with F^(m) , for T = A, (T¢ z)(x) = z¢ Tx = z¢ Ax = (A¢ z)¢ (x), for all x e Fⁿ and z e F^m. Hence T¢ could be identified with the ordinary transpose of the matrix A when T = A, a reason for the nomenclature 'transpose'.

PROBLEMS

1. Describe T¢ , if T equals: (a) 0, the zero transformation from V to W ; (b) I, the identity operator from V to V ; and (c) f, a linear functional from V to F.

2. If T is a linear transformation, show that the transormations T ® T¢ and T ® T¢ ¢ are non-singular.

3. If T is a linear operator on a finite dimensional vector space V , show that T, T¢ and T¢¢ have the same characteristic and minimal polynomials and the same eigenvalues with the same algebraic and geometric multiplicities.

4. Let V be a finite dimensional vector space over a field F, b a basis of V and b ¢ the basis dual to b . Let F as a vector space over itself have its standard basis e = {1}. Let f e V ¢. Determine [f]b ¢ , [f]b º [f]b _,e and the relation between [f]b ¢ and ([f]b )¢ ?

5. Let V and W be finite dimensional and T e L(V , W ). If [T]b denotes the matrix of T with respect to a pair of ordered bases b V and b W of V and W and [T¢]b ¢ the matrix of T¢ with respect to the dual bases b W ¢ and b V ¢, show that [T¢]b ¢ = [T]b ¢.

6. Describe T¢ and T¢f explicitly and compute (T¢f)(v) if :

(a) T(a, b, c) = a+b+c, f(a) = -a, v = (1, 2, 3);

(b) T(a, b, c) = (a+b, b+c), f(a, b) = b-a, v = (-1, 1, -1); and

7. Let V be the vector space of polynomials over R , D denote the differentiation operator: Dp(x) = p¢(x) and J the indefinite integral operator: Jp(x) = ò _[0,x] p(t)dt. Give an explicit description of D¢ and J¢ and find [D¢J_a –JD_a¢]p, if J_ap = Jp(a) and D_a p = Dp(a).

8. Let T and S be linear operators on a vector space V such that for some non-zero a Î V , Ta = Sa. Prove that there is a non-zero linear functional f on V such that T¢f = S¢f.

9. If V is a finite-dimensional vector space, prove that T ® T^t is an isomorphism of L(V , V ) onto L(V ¢, V ¢). Is the statement true if V is not finite dimensional?

10. If V is the vector space of n´ n matrices over a field F and P is any n´ n permutation matrix, veriy that: (a) for each B Î V , f_B(A) = trace (B¢AP), A Î V , defines a linear functional on V ; (b) every linear functional on V is an f for some B; and (c) B ® f_B is an isomorphism of V onto V ¢.

11. Let A be an m´ n matrix with real entries. Are AA^t and A^tA defined if A^t denotes the transpose of the matrix transformation A from R ⁿ to R ^m? Are AA¢ and A¢A defined if A¢ denotes the transpose of the matrix A?

12. Let i_n : Fⁿ ® F⁽ⁿ⁾ be defined by i_n x = x¢. If A denotes an m´ n matrix transformation and A¢ the transpose of A, find the matrix of the operator T_A = i_n^-1A¢i_mA on Fⁿ in the standard ordered basis and prove that trace (T_A) = 0 iff A = 0.

13. Determine the transpose of the differentiation operator D on the vector space of real polynomials of degree not exceeding n. Determine R (D¢) and N (D¢) and a basis for each of these.

Invariant Subspaces and Direct Sum of Operators

Let T be a linear operator on a vector space V . A subspace W of V is called invariant with respect to T or simply T-invariant if TW = {Tw : w e W } Ì W (i.e., the action of T on W does not take one outside W ).

Thus if A =, and B =, the subspace F₁ of F² spanned by e₁ is A-invariant but not B-invariant.

If W is T-invariant, T could be regarded as an operator on W in its own right. This defines the operator T|W : W ® W , the restriction of T to W by the rule (T|W )w = Tw, w Î W . Note that if W is not T-invariant T|W is not defined as an operator from W to W , but could still be regarded as a linear transformation from W regarded as a vector space to the vector space V .

If T is a linear operator on a vector space V , a T-invariant suspace W of V is said to possess a T-complementary subspace if there exists another T-invariant subspace W _c such that V = W Å W _c . For example the one dimensional A-invariant subspace F₁ considered above, has an A-complementary subspace iff c ¹ a, or, b = 0.

A direct sum decomposition V = W ₁ Å W ₂ Å … Å W _k of the vector space V is called a T-invariant direct sum decomposition, or simply an invariant direct sum decomposition, provided the operator T under consideration is implicitly understood, if each W _i is T-invariant. In this case if T_i = T|W _i , one writes T = T₁ Å T₂ Å … Å T_k , and says that the operator T is a direct sum of the operators T_i .

An invariant direct sum decomposition of V enables one to reduce a problem concerning the operator T by transferring it to the lower dimensional problems for the operators T_i on the vector spaces W _i 's. In this connection the following result is evident:

THEOREM. If V = W ₁ Å W ₂ Å … Å W _k is a T-invariant direct sum decomposition of V , b _i is a basis of W _i and T_i is the restriction of T to W _i and b denotes the pooled basis {b ₁, b ₂, … , b _k}, then [T]b = diag ([T₁]b 1, [T₂]b 2 , ... , [T_k]b k ).

The Projection operators E_i , 1 < i < k, associated with a direct sum decomposition V = W ₁ Å W ₂ Å … Å W _k, are defined as follows. A vector v Î V can be uniquely written as v = w₁ + w₂ + … + w_k, where w_i e W _i . Writing E_i v = w_i, it follows that, for 1 £ i £ k: (1) E_i is a linear operator with range W _i; (2) E_i² = E_i; (3) E_i E_j = 0, i ¹ j; and, (4) I = E₁ Å E₂ Å … Å E_k.

In general, a linear operator P on a vector space V is called a projection if P² = P. If P is a projection it is easily verified that N (P) = R (I-P) and N (I-P) = R (P), that V = R (P) Å N (P), and that P and I-P are the projections associated with this direct sum decomposition. One says that P is a projection of V on the subspace R (P) along the subspace R (I-P) = N (P).

PROBLEMS

1. Let E be a projection (E² = E) of V and let T be a linear operator on V . Prove that the range of E is invariant under T if and only if ETE = TE and that the null space of E is invariant under T iff ETE = ET. Hence deduce that both the range and the null spaces of E are invariant under T if and only if ET = TE.

2. Let A Î C ²´ 2, and W = {(x, x)¢ : x Î C } Ì C ². Find conditions on a₁₁, a₁₂, a₂₁, a₂₂ such that W has an A-complementary subspace.

3. If T is a linear operator on a finite-dimensional vector space V , verify that R = R (T), the range of T, and N = N (T), the null space of T, are T-invariant and that V = R Å N iff R Ç N = {0}.

4. Let V = W ₁ Å W ₂ Å … Å W _k, where each W _i is invariant under a linear operator T. Express (a) the determinant, (b) the characteristic polynomial, and, (c) the minimal polynomial of T in terms of those for the restriction operators T_i = T|W _i .

5. If E_i, 1 £ i £ m, are projections such that E₁ + … + E = I, prove that T = c₁E₁ + … + c_kE_k, where c_i 's are scalars, is diagonalizable and conversely.

6. Characterize linear operators on a finite dimensional vector space V which commute with every projection operator on V .

7. Let P denote the space of all polynomials on (-¥ , ¥ ) and P _e and P _o denote the subspaces of even, respectively, odd polynomials. (a) Show that P = P _e Å P _o. (b) If T is the indefinite integral operator (Tf)(x) = ò _[0,x] f(t) dt, and D the differential operator Df(x) º df(x)/dx, for which of the operators T, D, T², D², … , are P _e and P _o invariant?

8. Can a T-invariant W possess two distinct T-complementary subspaces?

Norms on Finite Dimensional Real or Complex Vector Spaces

A norm on a vector space V over a real or complex field K is a map P .P : V ® [0, ¥ ) satisfying: for x, y Î V and c Î K , (a) P xP = 0 iff x = 0; (b) P cxP = |c|P xP (homogeneity); and, (c) P x+yP £ P xP + P yP (triangle inequality). A vector space, with a norm defined on it, is called a normed linear space, or just a normed space. It is called real if K = R , and, complex if K = C .

The axioms of a metric or a distance function on a set M are: d(., .) : M ´ M ® [0, ¥ ), such that for x, y, z Î M, (a) d(x, y) = 0 iff x = y; (b) d(x, y) = d(y, x) (symmetry); and (c) d(x, z) £ d(x, y) + d(y, z) (triangle inequality). A set M along with a metric d(., .) on it constitutes a metric space.

A normed space (V , K , P .P ) has a natural metric associated with it given by: d(x, y) = P x-yP . It is termed as the metric induced by the norm in V .

By the convergence of a sequence {x^(k)} ® x in a metric d(., .) we mean d(x^(k), x) ® 0, as k ® ¥ . Convergence in a norm means convergence in the metric induced by the norm, described above.

Examples of Norms: Let V = K ⁿ ' x = (x₁, x₂, … ,x_n)¢.

(a) P xP ¥ = max {|x_j|: 1 £ j £ n} (max or sup -norm).

(b) P xP ₂ = Ö (x* x) = (S ₁£ j£ n |x_j|²)^1/2(l₂ , Euclidean (K = R ), unitary (K = C ) -norm).

(d) More generally, for p ³ 1, the l_p -norm: P xP _p = (S ₁£ j£ n |x_j|^p)^1/p, of which the above norms are special cases, (where we note that lim_p® ¥ P xP _p ® P xP ¥ ).

PROBLEMS

1. Prove that a positive multiple of a norm and the sum of two norms is a norm. Is the geometric mean of two norms a norm?

2. Consider all possible positive numbers a and b. For what pairs of a, b is the function N(x) = (S ₁£ i£ n |x_i|^a)^b a norm on K ⁿ? For what a, b is d(x,y) = (S ₁£ i£ n |x_i –y_i |^a)^b a metric on K ⁿ?

3. Find all norms on K and show that P xP /P yP , x, y Î K , does not depend on the choice of the norm.

4. Consider R ⁿ with the Euclidean. Let K be a closed and convex neighborhood of origin in R ⁿ such that x Î K implies that -x Î K (i.e., K is symmetric about the origin). Show that K defines a norm on R ⁿ by declaring its boundary to be the unit ball. Show also that every norm on R ⁿ arises in this fashion.

The Hölder and Minkowski's Inequalities

Hölder's Inequality. Let x, y Î R ⁿ and x_i, y_i ³ 0, 1 £ i £ n. Let 1 < p < ¥ , and, 1/p + 1/q = 1 (i.e., q = p/(p-1)). Then: S _{1£ i£ n} x_i y_i £ (S _{1£ i£ n} x_i^p)^1/p (S _{1£ i£ n} y_i^q)^1/q, where the equality holds iff the vectors x^p º (x₁^p, x₂^p, … , x_n^p)¢ and y^p º (y₁^p, y₂^p, … , y_n^p)¢ are linearly dependent.

Proof: If x, or, y equals 0 the result is trivial, and so is the case if n = 1. Hence, using induction on n, we may assume the result for R ^m, with m < n and work with x, y ¹ 0. We note that the quotient Q_n(x, y) = (S _{1£ i£ n} x_i y_i) / [(S _{1£ i£ n} x_i^p)^1/p (S _{1£ i£ n} y_i^q)^1/q], is invariant with respect to multiplication of x and y by positive scalars. Hence, as we are to prove that Q (x,y) £ 1, with equlality iff x^p, y^p ¹ 0 are linearly dependent, without loss of generality we could restrict ourselves to the region R_n defined by: R_n = {x, y Î R ⁿ: 1 £ S _{1£ i£ n} x_i^p, S _{1£ i£ n} y_i^p £ 2, x_i, y_i ³ 0}. Since R_n is a bounded and closed region in R ⁿ ´ R ⁿ, and Q_n(x, y) is a continuous function on it, it attains its maxima at some point of R_n. Note that, since ¶ Q/¶ x_j = [y_j - x_j^p-1 S _{1£ i£ n} x_i y_i )/( S _{1£ i£ n} x_i^p)]/D, and ¶ Q/¶ y_k = [x_k - y_k^q-1 S _{1£ i£ n} x_i y_i )/( S _{1£ i£ n} y_i^p)]/D, where D = [(S _{1£ i£ n} x_i^p)^1/p (S _{1£ i£ n} y_i^q)^1/q], Q(x, y) does not attain its maximum at a boundary point in R_n at which some x_j, or, y_k equals zero but the corresponding y_j, or, x_k is positive, as in this case Q increases towards R_n. If, however, also the corresponding y_j, or, x_k equals zero, we are reduced to a problem in R_m with m < n. Hence, in view of the invariance of Q with respect to the scalar multiplications, without loss of generality, we can assume that the maximum of Q is attained at an interior point in R_n. By the theory of lacal maxima and minima then ¶ Q/¶ x_j = 0 and ¶ Q/¶ y_k = 0, 1 £ j, k £ n, each of which is equivalent to x^p and y^q being linearly dependent. For computing the local maximum we can assume that x^p = y^q (due to invariance with respect to scalar multiplication). As x^p = y^q means y_i^q = x_i^p, so that x_iy_i = x_i^1+p/q = x_i^1+p-1 = x_i^p for 1 £ i £ n, in this case Q(x,y) = 1. The result follows. #

Corollary. If x_i, y_i ³ 0 and S _{i³ 1} x_i^p, S _{i³ 1} y_i^q < ¥ , the series S = S _{i³ 1} x_iy_i converges and S £ (S _{i³ 1} x_i^p)^1/p(S _{i³ 1} y_i^q)^1/q.

Minkowski's Inequality. Let x, y Î R ⁿ and x_i, y_i ³ 0, 1 £ i £ n. If 1 £ p < ¥ , then: [S _{1£ i£ n} (x_i+y_i)^p]^{1/p £}(S _{1£ i£ n} x_i^p)^1/p + (S _{1£ i£ n} y_i^p)^1/p, with the equality iff the vectors x and y are linearly dependent.

Proof: If p = 1, the inequality follows from the triangle inequality. So let p > 1. Writing S _{1£ i£ n} (x_i+y_i)^p = S _{1£ i£ n} x_i(x_i+y_i)^p-1 +S _{1£ i£ n} y_i(x_i+y_i)^p-1, and using the Hölder's inequality for the first term on the right, S _{1£ i£ n} x_i(x_i+y_i)^{p-1 £}(S _{1£ i£ n} x_i^p)^1/p (S _{1£ i£ n} (x_i+y_i)^(p-1)q)^1/q = (S _{1£ i£ n} x_i^p)^1/p (S _{1£ i£ n} (x_i+y_i)^p)^1/q. Similarly, for the second term we have the inequality S _{1£ i£ n} y_i(x_i+y_i)^{p-1 £}(S _{1£ i£ n} y_i^p)^1/p (S _{1£ i£ n} (x_i+y_i)^p)^1/q.

The Minkowski's inequality follows after adding these two inequalities and dividing both sides by (S _{1£ i£ n} (x_i+y_i)^p)^1/q.

For the equality, we must have the equality in the two inequalities in the above, i.e., the pairs x^p, (x+y)^p and y^p, (x+y)^p be linearly dependent, which is easily seen to be the case iff x and y are linearly dependent. This completes the proof. #

Corollary. The set l_p of infinite sequences x = {x₁, x₂, … } over K , for which S _{i³ 1} |x_i|^p < ¥ , where 1 £ p < ¥ , is a normed vector space over K , with component-wise addition and scalar multiplication and with the norm defined by P xP = (S _{i³ 1} |x_i|^p)^1/p.

Equivalence of Norms on Finite Dimensional Spaces

If h is an isomorphism from a vector space U to a vector space V and P .P is a norm on V then P .P defined by P xP = P h (x)P is a norm on U , induced by the norm P .P in V .

Theorem. All norms on a finite dimensional vector space V are equivalent, in the sense that for any two norms P .P _A and P .P _B there exist positive constants p, q such that pP xP _A £ P xP _B £ qP xP _A for all x e V .

Proof: Due to the isomorphism of an n-dimensional vector space over K with K ⁿ, it is sufficient consider the case when V = K ⁿ , P .P _A = P .P ¥ and P .P _B = P .P , the latter being any norm on K ⁿ. Let e_i, 1 £ i £ n, denote the standard unit vectors in K ⁿ. By the triangle inequality, P xP = P (S _{1£ i£ n} x_ie_i ) P £ S _{1£ i£ n} |x_i|P e_iP£ P xP ¥ S _{1£ i£ n} P e_iP= qP xP ¥ , say.

If the reverse type inequality does not hold, i.e., there is no positive number p such that pP xP ¥ £ P xP , for all x Î V , then there is a sequence {x^(m) Î V }_{m³ 1} for which P x^(m) P ¥ /P x^(m) P ® ¥ . Using the homogeneity poroperty: P cxP = cP xP , of any norm, without loss of generality, we may assume that P x^(m) P ¥ = 1, for all m. Then, by the Bolzano-Weierstrass principle {x^(m)} has a P .P ¥ -convergent subsequence ® x⁽⁰⁾ ¹ 0, say. For the subsequence we shall use the same notation as {x^(m)}. Then,

P x^(m)P³ P x^(0)P-P x^(m) -x^(0)P³ P x^(0)P- S _{1£ i£ n} |x^(m)_i - x⁽⁰⁾_i|P e_iP® P x^(0)P¹ 0, as m ® ¥ .

Hence, the sequence {P x^(m)P} is bounded away from zero, and since P x^{(m)P ¥}= 1, it follows that P x^{(m)P ¥}/ P x^(m)Pcan not diverge to ¥ , a contradiction. #

Corollary. If V is a finite dimensional vector space over K and V ' x^(m) ® x Î V , as m ® ¥ , in some norm then x^(m) ® x, as m ® ¥ , in any norm in V .

Matrix Norms

A norm P .P on the space K ⁿ´ n of nxn matrices over K is called a matrix norm, if in addition to the norm axioms, it also satisfies P ABP £ P AP P BP , for all A, B Î K ⁿ´ n.

As is easily verified, a norm on K ⁿ, i.e., on the n´ 1 vectors, induces a norm on K ⁿ´ n by defining

P AP = sup_x¹ 0 P AxP /P xP = max {P AxP : P xP = 1}, A Î K ^{n´ n}.

Since it means that P AxP £ P AP P xP , we have P (AB)xP = P A(Bx)P £ P AP P BxP £ P AP P BP P xP , from which it follows that P ABP £ P AP P BP . Hence an induced norm on matrices is always a matrix norm.

The above notion of an induced norm could be generalized for rectangular matrices, and in general for linear operators T : U ® V , by defining P TP = sup_u¹ 0 P TuP /P uP , where P TuP refers to a norm on V and P uP to the norm on U . Then if S : V ® W , with the induced norm P SP = sup_u¹ 0 P SvP /P vP , we have P STuP £ P SP P TuP £ P SP P TP P uP , where P SvP refers to a norm on W , implying that P STP £ P SP P TP .

Examples. Let the matrix norms induced by the vector norms P .P ₁, P .P ₂, and P .P ¥ be denoted by the same notations. Then

(i) P AP ₂ = Ö r (A* A) = P AP _S, (spectral-norm);

(ii) P AP ¥ = max₁£ i£ n S ₁£ j£ n |a_ij|, (max. absolute row-sum);

(iii) P AP ₁ = max₁£ j£ n S ₁£ i£ n |a_ij|, (max. absolute column-sum).

To prove these forms of the respective induced norms, we have: (i) P AP ₂² = max_x¹ 0 (Ax, Ax)/(x,x) = max_x¹ 0 (A* Ax, x)/(x, x) = r (A* A). (ii) P AP ¥ = max_i { |S ₁£ j£ n |a_ijx_j|: max_j |x_j| = 1} £ max_i S ₁£ j£ n |a_ij| = M, say. If this maximum is attained for i = k, say, then choosing x by x_j = sgn a_kj, j = 1, 2, … , n, where sgn z = |z|/z, for z ¹ 0, and zero if z = 0, we find P AP ¥ ³ M, so that P AP ¥ = max_i S ₁£ j£ n |a_ij|. Finally, (iii) P AP ₁ = max {S ₁£ i£ n |S ₁£ j£ n a_ijx_j|: S ₁£ j£ n |x_j| = 1} £ max {S ₁£ j£ n (S ₁£ i£ n |a_ij|) |x_j|: S ₁£ j£ n |x_j| = 1} £ max_j S ₁£ i£ n |a_ij| = N, say. If N is attained for j = k, with x_j = d _jk , j = 1, 2, … , n, we have P AxP ₁ = S ₁£ i£ n |S ₁£ j£ n a_ijx_j| = S ₁£ i£ n |S ₁£ j£ n a_ijd j| = S ₁£ i£ n |a_ik| = N, so that, as P xP ₁ = 1, also P AP ₁ ³ N. Hence, P AP ₁ = max₁£ j£ n S ₁£ i£ n |a_ij|. #

The Frobenius norm P AP _F of A Î C ⁿ´ n is defined by: (AP _F)² = tr(A* A), i.e., P AP _F = Ö (tr(A* A)). As, tr(A* A) = S ₁£ i£ n S ₁£ j£ n |a_ij|², P AP _F ³ 0 and P AP _F = 0 iff A = 0. Further, P cAP _F = |c|P AP _F is clear. For proving the triangle inequality: |tr(A* B)| = S ₁£ i£ n |S ₁£ j£ n a_ji* b_ji | £ P AP _F P BP _F, by Cauchy-Schwarz inequality. Similarly, |tr(B* A)| £ P AP _F P BP _F. Hence, P A+BP _F² = P AP _F² + tr (A* B) + tr (B* A) + P BP _F² £ (P AP _F + P BP _F )², showing that the triangle inequality, P A+BP _F £ P AP _F + P BP _F, holds.

To prove that P .P is a matrix norm, P ABP _F² = tr((AB)* AB) = tr (B* A* AB) = tr(A* ABB* ). Since the trace functional is invariant under a unitary transformation A* A could be taken to be diagonal D, and BB* a p.s.d. P. Then as d_i, p_ii ³ 0, P ABP _F² = tr (DP) = S ₁£ i£ n d_ip_ii £ (S ₁£ i£ n d_i)( S ₁£ i£ n p_ii) = P AP _F² P BP _F²,

proving that P ABP £ P AP P BP .

Note, however, that P .P _F is not an induced norm for n ³ 2. This may be seen, e.g., by noting that P IP _F = n, whereas for any induced norm P .P , P IP = max { P IxP : P xP = 1 } = 1. [Note that (P .P _F /n), n ³ 2, fails to be a matrix norm at all! (e.g., take A = diag (1, 0, … ,0) = B, to get the contradiction 1/n £ 1/n²).]

A matrix norm on C ⁿ´ n is called unitarily invariant if P AP = P AUP = P UAP , for every A Î C ^{n´ n} and unitary U Î C ^{n´ n}.

Theorem. The Frobenius norm P AP _F = (tr A* A)^1/2 and the spectral norm P AP _S = (r (A* A))^1/2 are unitarily invariant. If P .P is any unitarily invariant matrix norm, there holds the inequality P AP ³ P AP _S for any A Î C ^{n´ n}.

Proof: P AUP _F² = tr (AU)* AU = tr (U* A* AU) = tr (A* AUU* ) = tr A* A =P AP _F² . P UAP _F = tr (UA)* UA = tr (A* U* UA) = tr(A* A) = P AP _F² . P UAP _S² = r ((UA)* UA) = r (A* A) = P AP _S² . Also, P AUP _S² = r ((AU)* AU) = r (U* A* AU) = r (A* A) = P AP _S² . Finally, let A = UL V* (s.v.d.). Then for a unitarily invariant matrix norm P .P , P AP = P UL V* P = P L V* P = P L P ³ r (L ) = (r (AA* ))^1/2 = (r (A* A))^1/2 = P AP _S . #

PROBLEMS

1. Let A be an n´ n complex matrix and W unitary. Show that AW is positive definite iff P A-WP _F £ P A-UP _F for all unitary U.

2. Prove that r (A) £ P AP _S £ P AP _F .

3. Is P AP _L¥ = max |a_ij| a matrix norm on C ⁿ´ n?

4. For what p ³ 1 is P AP _Lp = (S ₁£ i£ n S ₁£ i£ n |a_ij|^p)^1/p a matrix norm on C ⁿ´ n? Is the answer 1 £ p £ 2, for n > 1?