Inner Product Spaces

Inner product spaces (IPS) are generalizations of the three dimensional Euclidean space, equipped with the notion of distance between points represented by vectors and angles between vectors, made possible through the concept of an inner product. These are broadly categorized as - real inner product spaces and complex inner product spaces and may be defined as follows. Let K commonly denote any of the fields R, or, C. Let V be a vector space over K. A map (. , .) : V ´ V ® K, satisfying: (a) (x, x) ³ 0, and (x, x) = 0, iff x = 0; (b) (x, y) = (y,x)* (star denoting complex conjugate); and, (c) (cx+y, z) = c(x, z) + (y, z), for all x, y, z Î V and c Î K, is called an inner-product in V.

Note that (a) asserts that (x, x) is a real number and is non-negative, even when K = C. A vector space V with an inner product on it is called an inner product space. If K = R, V is called a real inner-product space and if K = C, V is called a complex inner-product space. The scalar (x, y) is called the inner product of x and y. Note that in (b) the bar denotes complex conjugation, and so when K = R, (b) simply reads as (x,y) = (y,x). In the sequel, unless otherwise specified, an inner product refers to the field K which could be either of the fields R or C. Taking c = 1 in (c), (x+y, z) = (x,z) + (y,z). Putting x = 0 in it (0, z) = 0 and hence with y = 0 in (c), (cx,z) = c(x,z). The distributivity and conjugate linearity with respect to the second argument, namely (x, y+z) = (x, y) + (x, z), and (x, cz) = c(x, z), follow from the axiom (b) for an inner product.

Examples: In the following the verification of the inner product axioms is elementary and is left as an exercise.

(1) The Euclidean space Rⁿ and the Unitary space Cⁿ may be commonly defined as the inner product space Kⁿ over the field K, with the inner product given by (x, y) = y* x = S _{1£ i£ n} x_iy_i* , (x, y Î K ). This inner product is known as the standard inner product in K . In the sequel, unless otherwise specified, K would stand for the above standard inner product space. Note that when K = R, the complex conjugation is redundant and (x, y) = y¢x = x¢y. (2) The sequence space l₂(K) consisting of infinite square summable sequences x = (x₁, x₂, … , x_n, … ), i.e., S _{i³ 1} |x_n|² < ¥ , with the inner product (x, y) = S _{i³ 1} x_iy_i* , (x, y Î l₂(K)), is an infinite dimensional generalization of the inner product space K . (3) The space L₂(X, m ), over K, of functions f that are square integrable on a domain X with respect to the measure m , i.e., ò _X |f|² dm < ¥ , with the inner product (f, g) = ò _X fg* dm , is a further generalization of l₂(K).

The following is the most improtant result about an inner product:

Cauchy's inequality. If x, y Î V, an inner product space, |(x, y)|² £ (x, x)(y, y), with equality iff x and y are linearly dependent.

Proof: If x and y are linearly dependent, without loss of generality we may take y = l x, in which case both sides of the inequality equal |l |²(x, x) . If x and y are linearly independent, (by the axiom (a)) for any scalar l , 0 < (y-l x, y-l x) = (y, y) - 2Re [l (x,y)] + |l |²(x,x). Taking l = (y, x)/(x, x), this inequality reduces to 0 < (y,y) - |(x,y)|²/(x,x), which, since (x,x) > 0 (due to (a)), is equivalent to the Cauchy's inequality, with strict inequality, completing the proof. #

The Cauchy's inequality is also termed as Cauchy-Schwarz, or, Cauchy-Schwarz-Bunyakovsky inequality.

PROBLEMS

1. Verify the following for an inner product: (1) (0, y) = 0 = (x, 0); (2) (cx, y) = c(x, y), and (x, cy) = c* (x,y); (3) (cx, cx) = |c|² (x, x); (4) (S c_jv_j , v) = S c_j(v_j, v), and, (v, S c_jv_j) = S c_j* (v, v_j ); (5) (S a_iu_i, S b_jv_j) = S a_i S b_j* (u_i, v_j); (6) (x+y, x+y) = (x, x) + (y, y) + 2 Re(x,y); (7) if (x, y) = 0 for all x Î V, then y = 0; (8) if Re (x, y) ³ 0 for all x Î V, then y = 0; and, (9) if (x, y) = (x, z) for all x Î V, then y = z.

2. Show that the sum of two inner products on the same vector space V and a positive scalar multiple of an inner product on V is an inner product on V. Is the difference of two inner products an inner product?

3. Let (. , .) and (. , .) be two inner products on a vector space V. Show that there exist a scalar d such that (x, y) = (x, y) - c(x, y) is an inner product on V for all c < d, but for no c ³ d. How many such scalars d are there?

4. Describe explicitly all real inner products on R¹ and on C¹, and all complex inner products on C¹.

5. Let (. , .) be an inner product on a vector space V over C. Show that (. , .) continues to remain an inner product if V is regarded as a vector space over R.

6. Verify that the standard inner product on Kⁿ is an inner product and that it is characterized by (e_i, e_j) = d _ij, where e_i 's are the standard unit (basis) vectors.

7. Let {v₁, v₂, … , v_n} be an ordered basis of an inner product space V. Show than given any n-scalars c₁, … , c_n, there exists a unique v = S _{1£ i£ n} x_jv_j Î V such that (v, v_j) = c_j, 1 £ j £ n. Hence derive a system of linear equations for determining x_j 's.

8. Determine all linear operators T on Kⁿ for which (Tv, v) = 0 for all v.

9. If A Î K^{n´ n}, prove that f_A(x, y) = y* Ax is an inner product on the vector space Kⁿ over K iff A is positive definite, i.e., x* Ax is positive for all non-zero x Î C ⁿ.

10. Verify for an inner product that (u+v, u+v) + (u-v, u-v) = 2(u, u) + 2(v, v). Interpret this as saying that the sum of squares of lengths of diagonals equals the sum of squares of lengths of all the four sides of a parallelogram. Deduce Pythagoras theorem from this.

11. The matrix M of an inner product with respect to an ordered basis b is defined by: (u, v) = [v]b * M[u]b . If K = C (R), prove that M is hermitian (real symmetric) and is unique.

12. Show that (x, y) = x₁y₁ -3x₂y₁ -3x₁y₂ +10x₂y₂, defines an inner product on R². What is the matrix of this inner product relative to the standard basis in R²? What are all bases with respect to which the matrix of this inner product becomes the identity matrix?

13. For the real inner product (f, g) = ò _[0,1] f(t)g(t)dt, on L₂[0, 1], verify (S _{0£ j£ n-1} a_jx^j, S _{0£ k£ n-1} b_kx^k) = S _{0£ j,k£ n} (a_jb_k)/(j+k+1).

14. Prove that the Hilbert matrix (1/(i+j-1))_{1£ i,j£ n} is positive definite.

15. Determine the inner product on R², the quadratic form of which is given by P xP ² = (2x₁-3x₂)² + (3x₁-2x₂)².

16. If (u, v) is an inner product in Kⁿ such that |(u, v)| £ C|v*u|, for all u, v Î Kⁿ, where C is a constant, prove that (u, v) = cv*u, for all u, v Î Kⁿ, where c is a constant.

17. Which of (a) (x, y) = x* y, (b) (x, y) = y* x, (c) (x, y) = y¢x, and, (d) (x, y) = x¢y, is an inner product in Cⁿ? Which of these are inner products in R ⁿ.

18. Let {u_i}_{1£ i£ n} be a basis of an inner product space V. Show that <S, T> = S _{1£ i£ n} (Su_i, Tu_i) is an inner product in L(V).

19. Show that the standard basis {E_ij} of K^{n´ n}= L(Kⁿ), is orthonormal with respect to the inner product: <S, T> = S _{1£ i£ n} (Se_i , Te_i).

Norm Induced by an Inner Product

An inner product on a vector space V induces a natural norm in V by defining P xP ² = (x, x) , x Î V. Of the norm axioms: (a) P xP ³ 0, and P xP = 0 iff x = 0; (b) P cxP = |c|P xP ; and, (c) P x+yP £ P xP + P yP , (a)-(b) trivially follow from the inner product axioms. For the triangle inequality (c), we have P x+yP ² = P xP ² + P yP ² + 2 Re(x, y) £ P xP ² + P yP ² + 2|(x,y)| £ (P xP + P yP )², as follows from the Cauchy-Schwarz inequality.

In the sequel, unless otherwise specified, the norm in an inner-product space context would mean the induced norm defined as above. A sequence of vectors {x⁽ⁿ⁾} in a normed (vector) space V (over K) is called Cauchy if given any e > 0, there exists an N such that P x^(m) -x^(n)P < e , for all m, n > N. A sequence {x⁽ⁿ⁾} is said to converge if there exists an x Î V such that P x⁽ⁿ⁾ -xP ® 0, as n ® ¥ . A normed space V is said to be complete if every Cauchy sequence in it converges. A complete inner product space is called a Hilbert space. (In the literature, however, several authors exclude finite dimensional inner product spaces from being called Hilbert spaces). Bolzano-Weierstrass theorem and the equivalence of any two norms in a finite dimensional space imply that all finite dimensional vector spaces over K are complete. A subspace W of a normed space V is called closed if W ' w⁽ⁿ⁾ ® w, implies that w Î W (i.e., a sequence in W can converge only to an element in W itself).

PROBLEMS

1. Let V be an inner product space. For what real values of q does the function d(u, v) = (u-v, u-v)q , (u, v Î V), defines a distance in V, i.e., there hold: (1) d(u, v) ³ 0; (2) d(u, v) = 0 iff u = v; (3) d(u, v) = d(v, u) (symmetry); and, (4) d(u, w) £ d(u, v) + d(v, w), u, v, w Î V (triangle inequality).

2. Let V be a complex inner product space. If u, v Î V are such that (u, v) is real, i.e., u has a zero axial-twist with respect to y, show that P u+ivP ² = P uP ² + P vP ² and that u + iv is orthogonal to u - iv iff u is orthogonal to v and P uP = P vP .

3. Let V be an inner product space and G a finite dimensional subspace of V. Let v Î V\G and g Î G . Prove that P v-g_0P £ P v-gP , for all g Î G , i.e., g₀ is a best approximation of v from G, iff there exists an element u Î V such that (i) P uP = 1, (ii) (g, u) = 0, for all g Î G , and, (iii) (v, u) = P v-g_0P .

4. Let V be an inner product space and v₁, v₂, … , v_n Î V be linearly independent. Let G = < v₁, v₂, … , v_n >, the span of the vectors v₁, v₂, v₃, … , v_n. Show thatinf P v - gP = det ([(v_i, v_j)]_{0£ i,j£ n})/det ([(v_i, v_j)]_{1£ i,j£ n}] ).

5. Consider L₂(0,1), the Hilbert space of square integrable real valued functions on the interval (0,1) with the inner product (f, g) = ò _[0,1] f(x)g(x)dx. Let a _i > -1/2, 0 £ i £ n, and e_n = inf {P xa ⁰ - S _{1£ i£ n} c_ixa ^iP : c_i Î R}. Prove that e_n² = D ₀/D ₁ = [1/(2a ₀+1)]P _{1£ i£ n} {(a ₀ -a _i)²/(a ₀+a _i+1)}, where D _k = P _{k£ i<j£ n} {(a _i -a _j)²/P _{k£ i,j£ n} (a _i+a _j+1)} = det (1/(a _i+a _j+1)) _{k£ i,j£ n}. If 0 < a ₀ < a ₁ < … , deduce that any f Î L₂(0,1) can be approximated arbitrarily closely by linear combinations of the functions {xa ⁱ, i ³ 1} iff the series S _{i³ 1} a _i diverges.

6. Verify the parallelogram law for a norm induced by an innner product: P a+bP ² + P a-bP ² = 2P aP + 2P bP ².

7. In a complex IPS verify the polarization identity: 4(x,y) = P x+yP ² -P x-yP ² +iP x+iyP ² -iP x-iyP ².

8. In a real inner product space verify the identity: 4(x,y) = P x+yP ² -P x-yP ² .

Orthogonality in Inner Product Spaces

Let V be an inner product space. Given two vectors x, y in V, x is said to be orthogonal to y, if (x, y) = 0. Symbolically one writes x ^ y (read x is perpendicular, or orthogonal, to y). It is clear that x ^ y Û y ^ x. If in addition to being orthogonal, the vectors x and y are also normalized, i.e., PxP = PyP = 1, we say that x and y are orthonormal. A set S is said to be orthogonal to a set S ₂ (S₁ ^ S ₂) if s₁ ^ s₂ for all s₁ Î S₁ and s₂ Î S ₂.

A subset S of an inner product space is said to be orthogonal if u, v Î S and u ¹ v imply (u, v) = 0. A subset S is called orthonormal if in addition to being orthogonal, every element of it has unit norm. Every orhtonormal set is linearly independent, for if S c_iv_i = 0, taking inner product with v_j we get c_j = 0. It follows that an orthogonal set is linearly independent iff the zero vector does not belong to it.

A basis of an inner product space V which is orthonormal is called an orhonormal basis or a unitary basis of V. If a basis if just orthogonal it is called an orthogonal basis. A triangulization, or a diagonalization of a linear operator T on V by a unitary basis is referred to as a unitary triangulization, or unitary diagonalization.

PROBLEMS

1. Let T be a linear operator on a finite dimensional inner product space V. If Tu is orthogonal to u for all u Î V, show that T = 0.

2. Is it true that every inner product space V ¹ {0} has an othonormal basis?

3. Prove that any orthonormal set of vectors in an inner product space is linearly independent. Is the converse true?

The Angle Between Two Vectors

In view of the Cauchy-Schwarz inequality, for a real inner-product space, defining cos q = (x,y)/(||x||||y||), we have -1 £ cos q £ 1. Taking the principal value of q Î [0, p ], we get the notion of angle q between two vectors x and y, which coincides with the usual angle between two vectors in R ² and R ³. For a complex inner-product space V the notion of an angle between vectors, though not very neat, may however be defined as follows:

First of all let us consider a one dimensional subspace <v> = {cv: c Î K } spanned by a vector v of V . How does it look like? Unlike when the field K is R in which case <v> could be imagined as a line passing through origin, in the case K = C , it requires something like an imaginary surface of a right circular cylinder whose axis lies along the direction of v passing through the origin, so that assuming its base to be in the plane perpendicular to the axis through the origin and taking v to be represented by an arbitrary point on the surface at a positive height ||v|| marking the angle zero on the circle, the vector cv = re^iq v, (q Î [-p , p ]) could be represented as a point on the cylinder at signed height r and making angle q in the anticlockwise sense. The angle q could be imagined as an axial twist of cv over v. Then, interpreting the polar representation (x,y)/( P xP P yP ) = re^if , (-1 £ r £ 1, -p /2 £ f £ p /2), we find that the vector x has an additional minimal magnitude axial-twist of f radians over y. Thus if we wish to do meaningful real geometric operations compatible with the inner product we should work with the pair of vectors e^-if x, y, or, the vectors x, e^if y, the cosine of the real angle q between which is given by cos q = r Î [-1,1]. The principal value of q Î [0, p ] then may be defined as the required angle between x and y. In the case of real inner-product spaces this notion is compatible with the standard one.

PROBLEMS

1. Show that given any basis in a vector space V over K, there exists an inner product on V with respect to which the basis members are orthonormal.

2. If w Î Rⁿ, w¢ w = 1 and A = I - 2ww¢ , show that A reflects vectors in the hyperplane H = {x Î Rⁿ: w¢ x = 0} and is an orthogonal matrix. Interpret the complex case w Î Cⁿ.

Gram-Schmidt Orthonormalization Procedure

Given a sequence {v₁, v₂, … , v_m} of linearly independent vectors in an inner product space, the Gram-Schmidt procedure constructs another sequence {u₁, u₂, … , u_m} of vectors such that span {v₁, v₂, … , v_k} = span {u₁, u₂, … , u_k}, k = 1, 2, … , m, while in addition the vectors u_i 's are orthonormal: (u_i, u_j) = d _ij, i, j = 1, 2, ... , m. The construction goes as follows: Put u₁ = v₁/P v_1P and for i = 2, 3, ... , m, form the intermediate vectors w_i = v_i - S _{1£ j<i-1} (v_i, u_j)u_j and put u_i = w_i/P w_iP .

From the above construction it is clear that w_i, u_i belong to the span of{v₁, v₂, … ,v_i}, w_i ¹ 0 and that P u_iP = P w_iP /P w_iP , 1 £ i £ m. Further, since u_i is a non-zero scalar multiple of w_i, to prove (u_i, u_k) = 0, i ¹ k, it is sufficient to prove that (w_i,u_k) = 0, i > k. For this: (w_i,u_k) = (v_i, u_k) - S _{1£ j£ i-1} (v_i,u_j)(u_j, u_k) = (v_i, u_k) - S _{1£ j£ i-1} (v_i,u_j)(d _jk)= (v_i, u_k) - (v_i, u_k) = 0, completing the proof. #

Note that if the v_i 's are linearly dependent, for definiteness, say, if k is smallest such that v₁, v₂, … , v_k are l.d. then w_k becomes zero and the Gram-Schmidt process breaks down, and conversely. Thus, the G-S process could also be used to check the l.i. of vectors in an i.p.s.

Corollary. Every finite dimensional inner product space V (¹ {0}) has an orthonormal basis.

Proof: The G-S process applied to a basis gives an orthonormal basis. #

Unitary and orthogonal matrices have a very simple interconnection with a set of orthonormal vectors: An m´ n U is sub-unitary (sub-orthogonal) i.e., U* U = I, iff its column vectors u_j 's are orthonormal in Cⁿ (Rⁿ). Note that an m´ n U being sub-unitary (sub-orthonormal) implies that m ³ n and that when m = n, U becomes unitary (orthonormal) and then also UU* = I.

Theorem. If V and W are two n-dimensional inner product spaces over K, there exists an isomorphism h : V ® W, such that (h (x), h (y)) = (x,y), x, y Î V.

Proof: Take {v₁, v₂, … , v_n} and {w₁, w₂, … , w_n} to be orthonormal bases of V and W, respectively, and for x = S _{1£ i£ n} a_iv_i, defining h (x) = S _{1£ i£ n} a_iw_i, h is an isomorphism and with y = S _{1£ i£ n} b_iv_i, (h (x), h (y)) = (h S _{1£ i£ n} a_iv_i, h S _{1£ j£ n} b_jv_j) = (S _{1£ i£ n} a_iw_i, S _{1£ j£ n} b_jw_j) = S _{1£ i£ n} a_ib_j* = (x, y). #

Note that since the map h in the above theorem preserves the inner products, it preserves the distances and so it is an isometry. In particular, Taking W as Kⁿ, it follows that problems involving an n-dimensional inner product space can be isometrically transferred to the standard inner product space K ⁿ (i.e., R ⁿ, or C ⁿ).

The adjoint T* of a linear operator T : V ® W, where V and W are inner product spaces, is defined implicitly by the requirement (Tx, y) = (x, T*y), x Î V, y Î W, and is a linear operator from W to V. If V and W are finite dimensional inner product spaces, the existence, uniqueness and a construction of the adjoint is easy.

If T is a matrix operator A : K ⁿ ® K ^m, and as usual, A* for a complex matrix A denotes its adjoint matrix, i.e., the transpost of the complex conjugate of A, then for the standard inner products on K ⁿ and K ^m, (x, T* y) = (Tx, y) = (Ax, y) = (x, A* y) so that T* = A* , i.e., for a matrix operator over Euclidean or Unitary spaces with the standard inner products, the adjoint operator is nothing but the adjoint of the matirx.

Let V = {v₁, v₂, … , v_n} and W = {w₁, w₂, … , w_n} to be orthonormal bases of V and W, respectively. Let [x] = [x]V , [y] = [y]W , [T] = [T]V _,W . Then (Tx, y) = ([T][x], [y]) = ([x], [T]* [y]) = (x, T* y) implies that T* y = V [T]* [y] and that [T* ]W _,V = ([T]V _,W )* . Conversely, an operator T* from W to V defined by y ® V [T]* [y] satisfies (Tx, y) = (x, T*y), x Î V, y Î W is the same as the adjoint of T* .

Thus, the adjoint T* of T is the operator whose matrix with respect to a pair of orthonormal bases W , V is the adjoint of the matrix of T with respect to the pair V , W . T is called sub-unitary if T* T = I, the identity operator on V. T is said to be unitary if T* T = I and TT* = I (or equivalently that both T and T* are sub-unitary). A linear operator T on an inner product space V is called self adjoint if T* = T, unitary if T^*T = I (in which case the accompanying relation TT* = I automatically holds!) and normal if T* T = TT* , i.e., T and T* commute. In the case of a finite dimensional inner product space V, the self-adjoint, unitary and normal operators are easily associated with the corresponding matrices as follows:

Theorem. If T is a linear operator on a finite dimensional inner product space V, b is an ordered unitary basis of V and A = [T]b , then T is self-adjoint, unitary or normal according as A is.

Proof: Let b = {w₁, w₂, … , w_n}. For any u, v Î V, let x = [u]b , and y = [v]b . Then, (u, v) = (x,y), the standard inner product of x and y in Kⁿ. Hence (x,[T* ]b y) = (u, T* v) = (Tu, v) = (Ax, y) = (x, A* y), implying that A* = [T* ]b , from which the results are clear. #

Theorem. Let T be a linear transformation from an IPS V to an IPS W . Then N (T) ^ R (T* ) and R (T) ^ N (T* ).

Proof: Let u Î N (T) and v Î R (T* ). Then v = T* w for some w Î W . Hence, (u, v) = (u, T* w) = (Tu, w) = (0, w) = 0. Similarly, if w Î R (T) and v Î N (T* ). Then w = Tu for some u Î V . Hence, (w, v) = (Tu, v) = (u, T* v) = (u, 0) = 0. #

PROBLEMS

1. Let T : V ® W, both being inner product spaces with b and g being two unitary bases of the respective spaces. If A = [T]b _,g , show that [T* ]g _,b = A* , [T* T]g = A* A and [TT* ]b = AA* . Deduce that T is sub-unitary or unitary according as A is.

2. Let u₁, u₂, … , u_n and v₁, v₂, … , v_n be two bases in an inner product space. Let T and S be two linear operators such that (Tu_i, v_j) = (u_i, Sv_j), i, j = 1, ... , n. Prove that T = S* .

3. Let b be an orthonormal basis and A = [T]b , where T is a linear operator. Prove that A* = [T* ] . Does this result remain true if B is not necessarily orthonormal?

4. Prove that for a linear operator T on a finite dimensional inner product space V, the following statements are equivalent: (a) T is unitary; (b) (Tu,Tu) = (u, u), for all u Î V; (c) (Tu, Tv) = (u, v), for all u, v Î V.

5. Prove that a linear operator T on a finite dimensional inner product space V is normal iff ?Tu? = ?u?, for all u Î V.

Projections and Orthogonal Projections

A linear operator (or a matrix) P is called a projection (projection operator or a projection matrix) iff P² = P, i.e., P is idempotent. Writing I = P + (I-P) = P Å (I-P) is a direct sum in the sense that R (P)Ç R (I-P) = {0} and that R (P) and R (I-P) are invariant, respectively under P and I-P. To see this, if x Î R (P), then x = Py for some y and so Px = P²y = Py = x Î R (P), i.e., P is an identity operator on R (P). As, (I-P)² = I-2P+P² = I-P, I-P itself is a projection and I-P acts as an identity on R (I-P) which therefore is invariant under I-P. Now let R (P)Ç R (I-P) ' x = Py = (I-P)z. Then x = Py = P²y = (P-P²)z = 0. Hence R (P)Ç R (I-P) = {0}. Note that P, respectively, I-P act as null operators on R (I-P) and R (P).

Also we have V = R (P)Å R (I-P) and x = Px + (I-P)x, is the unique decomposition of an x Î V into elements of R (P) and R (I-P). Pooling up the bases of R (P) and R (I-P), it follows that a projection is diagonalizable and its eigenvalues are only 0 and 1's, and conversely. A projection P is called an orthogonal projection if R (P) ^ N (P) = R (I-P).

Theorem. A projection P is an orthogonal projection iff P* = P (i.e., P is self-adjoint).

Proof: P is orthogonal projection Û P is projection and (Px, (I-P)y) = 0 for all x, y Û P is projection and P* = P*P Û P is a projection and P = P*P = P* Û P is a projection and P* = P. #

Corollary 1. P is an orthogonal projection iff it is unitarily diagonalizable with eigenvalues 0 and 1's.

Proof: Self-adjointness implies normalcy, which implies unitary diagonalization. Eigenvalues 0 and 1's only and diagonalization implies projection property. Projection and unitary diagonalization implies projection and self-adjointness which is equivalent to orthogonal projection property. #

Corollary 2. If an m´ n A is sub-unitary (A*A = I, m ³ n) then AA* is an orthogonal projection.

Proof: (AA*)² = A(A*A)A* = AIA* = AA*. Hence AA* is a projection. But (AA*)* = (AA*). Hence AA* is also self-adjoint and hence an orthogonal projection. #

Theorem. If A is a projection matrix over F , tr(A) = r(A)1, where 1 is the unity in F .

Proof: Iff A is a projection, for some non-singular C, A = C^-1 diag (d₁, … , d_n) C, where d_i = 0, or, 1. Using tr AB = tr BA, we have tr A = tr (C^-1 diag (d , ... , d ) C) = tr (diag(d , ... , d ) CC^-1) = tr (diag(d₁, … , d_n)) = r(A)1. #

Corollary. If the field is of characteristic zero and I = E₁ + E₂ + … + E_k, where E_i 's are projections, then E_iE_j = 0, i ¹ j.

Proof: I = E₁ + … + E_k implies that V = E₁V + … + E_kV. Let W = E_iV, 1 £ i £ k. As dim W_i = rank E_i and S _{1£ i£ k} tr E_i = tr I, the characteristic of the field being zero, n = dim W₁ + ... + dim W_k . It follows that V = W₁ Å … Å W_k. Now, N (E₁) = R (I - E₁) = R(E₂ + … + E_k) and therefore N (E₁) Ì W₂ Å … Å W_k . But R (E₁) = W₁. Hence since W₁ Ç (W₂ Å … Å W_k) = {0} and V = R (E₁) Å N (E₁), N (E₁) = W₁ Å … Å W_k. It follows that E₁E_j = 0, j ¹ 1 (as (E₁E_j)v = E₁(E_jv) Ì E₁W_j ). By reordering, E₁ could be taken to be any of the E_i 's. Hence E_iE_j = 0, i ¹ j. #

PROBLEMS

1. Let V be an (n+1)-dimensional vector space over a field F and T a linear operator on V. Let c₀, c₁, … , c_n Î F be distinct. Let p(x) = P _{0£ i£ n} (x-c_i), and l_k(x), 0 £ k £ n denote the basic Lagrange interpolation polynomials given by l_k(x) = P _{j¹ k} [(x-c_j)/(c_k -c_j )], where j runs from 0 to n. Let E_k = l_k(T). Show that : (i) I = E₁ + E₂ + … + E_n; (ii) T = S _{0£ k£ n} c_kE_k ; (iii) if p(T) = 0, show that E_k 's are projections such that E_i E_j = 0, 0 £ i ¹ j £ n.

2. Find, using observations alone and without computations, an orthogonal basis of R⁴ one member of which is to be (1,1,1,1)¢. [Hint: Use 0, ± 1 as components.]

3. Let W be the subspace of R⁴ consisting of all vectors which are orthogonal to both u = (1, 2, 3, 4)¢ and v = (4, 3, 2, 1)¢ . What relations do the components of w Î W satisfy? Use these to find an orthonormal basis for W.

4. Use the Gram-Schmidt process on u = (1, 0, 0)¢, v = (1, 2, 0)¢, and w = (1, 2, 3)¢, to obtain an orthonormal basis for R³. Redo the problem with u = (1, 2, 3)¢, v = (1, 2, 0)¢, w = (1, 0, 0)¢. What do you conclude?

5. Find an orthonormal basis for the subspace of C³ spanned by u = (1, 0, i), and, v = (1, 0, -i), using observations only.

6. Let W be the subspace of R² spanned by the vector (11, 12)¢. and P denote the orthogonal projection of R² onto W. Find: (a) a formula for P(x₁, x₂)¢; (b) the matrix of P in the standard ordered basis; (c) W^ ; (d) an orthonormal basis in which P is represented by the matrix

.

Also, show that the matrix of P with respect to any orthonormal basis is of the obove type. Repeat (a)-(d) with another inner product on R the quadratic form of which is given by ?(x ,x )? = (2x₁ -x₂)² + (x₁ -2x₂)².

7. Find all inner product on R² such that (e₁, e₂) = 2, where e_i 's are the standard basis vectors.

8. Let V denote the vector space of real valued functions, square integrable with respect to a measure m on an interval I. Show that (f,g) = ò _I fgdm is an inner product on V. If every monomial belongs to V, show that there exists a unique sequence of monic polynomials P_n, n ³ 0, of degree n such that (P_n, P_m) = 0, n ¹ m. Prove that for all n ³ 1: (a) there exist scalars a_n, and, b_n such that P_n+1(x) = (x + b_n)P_n(x) + c_nP_n-1(x), n ³ 1; (b) c_n < 0; (c) all the n-zeros of P_n are real, simple and lie in the interior of the interval I; (d) between any two zeros of P_n+1 there lies a zero of P_n; (e) if Q_n is a polynomial of degree n such that (Q_n, R_n-1) is zero for all polynomials R_n-1 of degree £ n-1, then Q_n = cP_n for some scalar c; and (f) if P _n denotes the subspace of polynomials of degree £ n, show that the orthogonal complement of P _n in P _m equals the span of P_n+1, P_n+2, … , P_m, (m > n).

9. With dm (x) = w(x)dx, for the intervals I and weight functions as follows, compute the first four monic orthogonal polynomials: (a) I = [-1,1], w(x) = 1 (Legendre polynomials, P_n); (b) I = [-1,1], w(x) = 1/Ö (1-x²) (Tchebycheff polynomials, T_n); (c) I = [0, ¥ ), w(x) = e^-x (Laguerre polynomials, L_n); (d) I = (-¥ , ¥ ), w(x) = exp {-x²} (Hermite polynomials, H_n) and (e) I = [-1,1], w(x) = (1-x)a (1+x)b (Jacobi polynomials, J_n^{(a ,b )}).

10. Let V be the vector space of all n´ n matrices over C, with the inner product (A, B) = tr (AB* ). Find the orthogonal complement of the subspace spanned by: (i) diagonal matrices, (ii) real symmetric matrices, (iii) hermitian matrices, (iv) skew hermitian matrices, (v) real skew symmetric matrices, (vi) unitary matrices, (vii) non-singular matrices, (viii) lower triangular matrices, and (ix) upper triangular matrices.

11. If V is an inner product space, and v₁, … , v_n Î V, show that for all u, v Î V there holds (u, v) = S _{1£ k£ n} (u, v_k)(v_k,v), iff v₁, … , v_n are orthonormal and dim V = n.

12. Let P be a projection of an inner product space V on a finite dimensional subspace W. Show that (Pu, v) = (u, Pv) for all u, v Î V iff P is an orthogoanl projection.

13. For any subset S of an inner product space V, show that (S ^ )^ contains <S >, the subspace spanned by S . When <S > is finite dimensional, prove the equality (S ^ )^ = <S>. Give a counter example when <S > is not finite dimensional

14. If b = {v₁, … , v_n} is an ordered orthonormal basis of an inner product space V, show that the matrix A = [T]b of a linear operator T on V could be calculated from a_ij = (Tv_j,v_i).

15. Suppose V = W₁ Å W₂ and that f₁ and f₂ are inner products on W₁ and W₂, respectively. Let P be the projection of V on W₁ along W₂. Show that f(u, v) = f₁(Pu, Pv) + f₂((I-P)u, (I-P)v) is the unique inner product on V such that: (a) W₂ = W_1^ ; (b) f(u, v) = f_k(u, v), when u, v are in W_k , k = 1, 2; and, (c) P is the orhogonal projection of V on W₁.

16. Show that in an inner product space V, of all projections of V on a subspace W, the orthogonal projection on W is characterized by: P PvP £ P vP for all v Î V.

17. Consider the vector space C[-1,1] with the inner product (f, g) = ò _[-1,1] f(t)g(t)dt. Find the orthogonal complement of the subspace of even functions? What is the orhogonal complement of the subspace of odd functions? Repeat the exercise if the inner product is changed to (f, g) = ò _[-1,1] w(x)f(t)g(t) dt, where w(x) > 0 is general.

18. If P and Q are commuting (orthogonal) projections, then PQ is also (orthogonal) projection.

19. A hermitian matrix has only real eigenvalues and as a matrix operator it is self adjoint with respect to the standard inner product. Is is true that the eigenvalues of any self adjoint operator on a finite dimensioal inner product space are real?

20. Given a diagonalizable operator T on Rⁿ, does there always exist an inner product on Rⁿ with respect to which the eigenvectors of T are orthonormal?

21. For x = (x₁, x₂)¢, find T* x if the linear operator T on C is defined through: (a) Te₁ =(1, i)¢, Te₂ = (i, -1)¢; (b) Te₁ = (1+i, 1-i)¢, Te₂ = (1-i, 1+i)¢; and, (c) Te₁ = (1+i, i-1)¢, Te₂ = (1-i, 1+i)¢. Also determine the matrices of the operators T, T* and TT* -T* T in the standard ordered basis and describe the ranges and the null spaces of these operators and check if they are related?

22. Let T denote the linear operator on C³ whose matrix A in the standard ordered basis is defined by: a_jk = i^j-k, (i = Ö (-1)). Find orthonormal bases for the null spaces of T and T* .

23. Let V be a finite-dimensional inner product space and T a linear operator on V. Prove that V = R (T* ) Å ^ N (T) = R(T) Å ^ N(T* ), where W_{1 Å ^} W₂ means a direct sum in which the component subspaces are orthogonal to each other.

24. Let V be a finite-dimensional inner product space and T a linear operator on V. Prove that T is invertible iff T* is invertible and that there holds (T* )^-1 = (T^-1)* .

25. Let y = (y₁, … , y_n)¢ and z = (z₁, … ,z_n)¢ be two fixed vectors. If T is given by Tx = (x, y)z, x Î Cⁿ, determine the matrix of T in the standard ordered basis and find the range and null spaces of T* .

26. Show that the product of two self-adjoint operators T and S is self-adjoint if and only if their commutator TS-ST is so.

27. If {u_k}_{1£ k£ n} is an orthonormal basis of an inner product space V, show that Tv = S _{1£ kn} (v, T* u_k)u_k, for every linear operator T on V. If V = Kⁿ (K = R or C), deduce that: I = S _{1£ k£ n} u_ku_k* .

28. Consider the vector space of real polynomials of degree £ n with the inner product (P, Q) = ò _[0,1] P(x)Q(x) dx. If D denotes the differentiation operator and A the left averaging operator given by AP(x) = x ò _[0,x] P(t)dt, find D* and A* . Are they invertible?

29. In C^{n´ n} with the inner product (A, B) = tr (AB* ), determine T* if T is defined by: (a) TA = BA, (b) TA = AB, (c) TA = BAC, and, (d) TA = AB-CA+EAF.

30. Prove that a projection operator on a finite dimensional inner product space is self adjoint iff it is normal.

31. Show that a linear operator T on a finite-dimensional complex inner product space is self-adjoint if and only if (Tv, v) is real for every v Î V.

32. Find a unitary matrix which is not complex-orthogonal, and find a complex-orthogonal matrix which is not unitary.

33. Consider the vector space C^{n´ n} with the inner product (A, B) = tr (AB* ). For M, N Î C^{n´ n}, let T_M,N be the linear operator on C^{n´ n} defined by T_M,N (A) = MAN. Show that T_M,N is unitary if and only if nM/tr(M) and nN/tr(N) are unitary, and |tr(M)tr(N)| = 1.

34. Let Cⁿ(R) denote Cⁿ regarded as a real vector space.

(a) Show that (x, y) = Re (y* x) defines an inner product on C ⁿ(R).

(b) Exhibit an isometric isomorphism of Cⁿ(R) onto R ²ⁿ with the standard inner product.

(c) For each A Î C ^{n´ n}, let T_A be the linear operator on C ⁿ(R) defined by T_A(x) = Ax. Show that (T_A)* =T_A*

(d) For which complex A is T_A self-adjoint?

(e) For which A is T_A unitary?

(f) For which A is T_A positive definite?

(g) What is det (T_A)?

(h) Find the matrix of T in the ordered basis: {e₁, e₂, … , e_n, ie₁, ie₂, … , ie_n}.

(i) If T is a linear operator on C ⁿ(R), find necessary and sufficient conditions for T to be a T_A.

(j) Find a unitary operator on C ⁿ(R) which is not a T_A .

35. Considering R as the Euclidean plane, write down the transformation equations governing: (a) anti-clockwise rotation by an angle q about a point (x ,y )¢; (b) reflection in the line y = mx +c, where m = tan a.

36. Prove that the operation of rotating the plane about a point is a linear operation in R² iff the point is the origin.

37. Show that the operation of reflecting points in the plane in a line is a linear operation iff the line passes through the origin.

38. From the unitary isomorphism (x, y)¢ ® x + iy = z = re^iq , of R² onto C(R), it follows that a linear rotation (anti-clockwise) of the plane R by an angle f increases q by f so that a point P = (x, y)¢ moves to the point P = (x , h )¢, with z = re^{i(q +f )} = x + ih , so that x = x cos f - y sin f and h = x sin f + y cos f . Hence, show that the matrix T of this transformation, with respect to the standard ordered basis, is given by

T = .

39. Show that the reflection of a point in the x-axis in the plane R² corresponds to a linear operator whose matrix with respect to the standard ordered basis is given by

.

40. Prove that the operation of reflection about the line y = mx, (m = tan f ), is equivalent to a linear rotation by the angle -f , followed by a reflection in the x-axis and then another linear rotation by the angle f . Hence, or otherwise, show that this constitutes a linear operation in R whose matrix is given by

R_f = .

41. Prove that a linear rotation is never a reflection and a reflection is never a linear rotation, but that a product of linear rotations and linear reflections is either a linear rotation or a linear reflection.

42. Show that every unitary operator in R is either a linear rotation or a linear reflection.

43. Show that the adjoint of a linear rotation or a linear reflection is the inverse of the operator.

44. Prove that (a) a linear rotation followed by a linear rotation is a linear rotation, (b) a linear rotation followed by a linear reflection is a linear reflection, (c) a linear reflection followed by a linear rotation is a linear reflection, and that, (d) a linear reflection followed by a linear reflection is a linear rotation. Hence deduce that a product of linear rotations and linear reflections is a linear reflection if it has an odd number of linear reflections and that it is a linear rotation otherwise. Generalize for rotations about arbitrary points and reflections in arbitrary lines.

45. Let W be a subspace of a finite dimensional vector space V and let P denote the orthogonal projection on W. If U = 2P-I, show that U may be interpreted as a reflection of V in the subspace W and that U is both self-adjoint and unitary. If V = R and W is the span of the vector (1, 1, 1)¢ , find the matrix of U in the standard ordered basis and interpret U as a 180 -rotation about an appropriate axis.

46. If w Î Rⁿ is a unit vector (w¢w = 1), the n´ n matrix operator H = (I-2ww¢) is called a Householder rotation. Prove that H is actually a reflection in the hyperplane w^ , whereas -H is a reflecion in the w-axis, which for n ³ 3 may be regarded as a rotation about the w-axis.

47. If T is any self-adjoint linear operator on a complex inner product space V, prove that P v+iTvP = P v-iTvP = (P vP ² + P TvP ²)^1/2 , v Î V and deduce that I ± iT is non-singular and hence that if V is finite dimensional, the related Cayley transform of T, defined by U = (I-iT)(I+iT)^-1, is unitary. Relate the result with the fact that the conformal map f(z) = (1-iz)/(1+iz) takes the x-axis into the unit circle.

48. If q is a real number, prove that the matrices

A = , B = ,

are unitarily equivalent by finding a unitary U so that B = U* AU.

49. Find all matrices B unitarily equivalent to the matrix A in the previous problem.

50. Let V be a finite-dimensional inner product space and T a positive definite linear operator on V. Let [. , .] be another inner product on V defined by [u, v] = (Tu, v). Prove that U is unitary with respect to both the inner products iff U commutes with T.

51. Let u, w Î V, a finite-dimensional inner product space. If T denotes the linear operator on V defined by T_u,w(v) = (v, w)u, show that: (a) if u, w, g, h ¹ 0, T_u,w commutes with T_g,h iff the sets {u, g} and {w, h} are linearly independent; (b) T_u,w self adjoint iff one of u and w is a real scalar multiple of the other; (c) If u, w ¹ 0, T_u,w is diagonalizable iff trace (T_u,w) ¹ 0; (d) T_u,w is normal iff u and w are linearly dependent; (e) a linear operator T on V commutes with T_u,w iff for some scalar c, Tv = cv and T* v = c* v; and, (f) P T_u,wP = P uP P wP , where the norms are the ones induced by the inner product.

52. Let V be a finite dimensional inner product space and L(V) denote the vector space of linear operators on V. Prove that (T, S) = trace (S* T), T, S Î L(V), defines the unique inner product on L(V) for which P T_{u,wP F} = P uP P wP for all u, w Î V, where T_u,w(v) = (v, w)u, v Î V. (Frobenius norm).

53. Show that every self adjoint unitary operator on a finite-dimensional inner product space is a reflection in some subspace of V.

54 Let U Î L(V, W), where V and W are finite dimensional inner product spaces. Let U : V ® W be a linear operator. In each of the following cases find the minimal conditions on U so that: (a) the map T ® UTU* is an isomorphism of the algebra L(V,V) onto the algebra L(W,W); (b) trace (UTU* ) = trace (T), T Î L(V,V). (c) UT_u,wU* = T_Uu,Uw , where T_u,w(v) = (v, w)u; (d) (UTU^-1)* = UT* U^-1, assuming that U is invertible; (e) the map T ® UTU* preserves inner products in L(V,V) and L(W,W ) given by (T, S) = tr (S* T).

55. For the following real symmetric matrices A, find orthogonal matrices P such that P¢AP is diagonal:

.

56. Is the square of every complex symmetric matrix positive definite? Is it self-adjoint? Is it normal?

57. Show that there exist only a finite number of orthogonal matrices P that diagonalize the matrix

A = .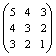

Hence describe all the matrices C such that C^-1AC is diagonal.

58. Show that the matrix A = is normal and find an orthonormal basis of C² of its eigenvectors.

59. Give examples of 3´ 3 matrices A such that A³ is: (a) normal, (b) hermitian, and (c) positive define, without A being so.

60. If T is a normal operator on a finite-dimensional inner product space, show that T is, respectively, self-adjoint, positive definite, or, unitary iff all the eigenvalues of T are real, positive, or, of absolute value 1.

61. If T is a normal operator on a finite-dimensional inner product space, prove that it is both self-adjoint and unitary iff T = I. When is T both positive definite and unitary?

62. Use spectral theorem to show that a linear operator T on an i.p.s. V is normal iff T = H₁+iH₂, where H₁, H₂ are commuting self-adjoint operators.

63. Show that T is self-adjoint iff it can be written as a difference of two positive definite operators: T = P₁-P₂.

64. If T is self-adjoint show that there exist unique p.s.d. P₁, P₂ such that T = P₁-P₂ and P TP ² = P P_1P ²+P P_2P ².

65. If m = 1, 2, … , prove that a real symmetric matrix A has a real symmetric (2m+1)-th root B (i.e., A = B^2m+1), which is also real symmetric and that it has a real symmetric 2m-th root iff it is postitive semi-definite.

66. Prove that every positive (semi-) definite matrix is the square of a positive (semi-) definite matrix.

67. Prove that a nilpotent operator is normal iff it is the zero operator.

68. Prove that an n´ n complex matrix A is normal iff A is diagonalizable and its eigenvectors vectors associated with distinct eigenvalues are orthogonal.

69. Is the sum of two commuting normal operators normal?

70. Is the product of two commuting normal operators normal?

71. Let a_i Î Cⁿ, i = 1, 2, ..., n, be linearly independent, P a_iP = 1, R_i = I-2a_ia_i* , A = R₁R₂ … R_n. Show that A-I is invertible. If H = (A+I )(A-I) , prove that a_i* Ha_i = 0, 1 £ i £ n. [Hint: If Ax = x, x ¹ 0, R₁^-1 = R_1* = R₁ Þ R₂R₃…R_nx = R₁x Þ x-2a₁a_1* x = x+S _{2£ j£ n} a _ja_j, a _j Î C, say. By l.i. of a_j 's, a_1* x = 0. Þ R₃…R_nx = R₂x. Þ a_2* x = 0. Continuing in this fashion, we get a_i* x = 0, 1 £ i £ n. Þ x = 0. Hence A-I is invertible. Next, let 1 £ i £ n, and (A-I_n)x = a_i. Put R = R_i+1 … R_n, and L = R₁ … R_i-1. Þ Rx-2a_ia_i* Rx = R_iRx = L^-1Ax = R_i-1…R₁(a_i+x), or, x+S _{i+1£ j£ n} b _ja_j -2a_ia_i* Rx = a_i+x+S _{1£ j£ i-1} b _ja_j , b _j Î C. By l.i. of a_j 's, Rx = x (b _i 's are zero), -2a_i* Rx = 1 and -2a_i* x = 1. Þ a_i* Ha_i = a_i* (A+I_n)(A-I_n)^-1a_i = a_i* (A+I_n)x = a_i* (a_i+2x) = (P a_{iP 2})² + 2a_i* x = 0. #]

72. If v₁, v₂, … , v_n are orthonormal, prove that Tu = S _{1£ i£ n} (u, v_i)v_i, is the orthogonal projection of u on the subspace G = <v₁, v₂, … , v_n> and, moreover, that Tu is the unique vector from G nearest to u.

THE KACZMARZ METHOD

Let C ⁿ and C ^m have some prescibed inner products. The Kaczmarz method is an iterative procedure for providing a solution of a consistent equation Ax = b deviating least from the starting initial vector. The method, nevertheless, converges even for an inconsistent system.

Orthogonal Projection on a Hyper Plane

Consider a hyper plane given by Rx = b , where R is a row vector and b is a scalar. The unit normal to the hyper plane is given by R* /P R* P and the orthogonal projection of a vector x on the hyper plane is obtained by removing the vector joining the foot of the perpendicular from x to its orthogonal projection on the hyperplane Rx = b . Here R* is the adjoint of the linear functional R, i.e., (Rx, y) = (x, R* y). Hence the projection has the form

z = x - q R* /P R* P ,

where q is obtained by the condition Rz = b , so that Rx - q RR* /P R* P = b , i.e., q = (Rx - b )/P R* P . Thus

z = x - (Rx - b )R* /P R* P ² = [I - R* R/P R* P ²]x + b R* /P R* P ² = [I - P_R*]x + b R* /P R* P ²,

where P_R* denotes the orthogonal projection on the span of R* .

The Kaczmarz method

The Kaczmarz method for Ax = b, where A is an m´ n complex matrix begins with an initial vector x⁽⁰⁾ and generates a sequence of iterations x^(k), k ³ 1 as follows. The vector x^(k) is orthogonally projected on the i-th hyperplane R_ix = b_i, for 1 £ i £ m, to arrive at x^(k+1), the expression for which is given by

,

where Q_i = [I - P_Ri*], the orthogonal projection on the othogonal complement of the subspace spanned by R_i* . It is clear that

= Hx^(k) + c,

say, where c Î R (A* ), A* being the adjoint of the matrix operator A : R ⁿ ® R ^m. Since, R (A* ) = N (A)^ ,

Q_i = [I - P_Ri*] : R (A* ) ® R (A* ), 1 £ i £ m,

and

Q_ix = x, x Î N (A), 1 £ i £ m,

i.e., Q_i is an identity on N (A). Hence Q_ix = Q_i[PR _(A*)x + PN _(A)x] = Q_i[PR _(A*)x] + PN _(A)x, x Î C ⁿ.

It follows that Hx = H[PR _(A*)x] + PN _(A)x. If P H[PR _(A*)x]P = P PR _(A*)xP , then writing z = PR _(A*)x, Q_iz = z, 1 £ i £ m, so that R_iz = 0, 1 £ i £ m, i.e., Az = 0, or that z Î N (A). But z Î R (A* ), so that z = 0. Hence the restriction of H to R (A* ) has norm less than 1, so that

lim_{k® ¥} H^kx⁽⁰⁾ = lim_{k® ¥} H^k PR _(A*)x⁽⁰⁾ + PN _(A)x⁽⁰⁾ = PN _(A)x⁽⁰⁾.

Moreover, h = lim_{k® ¥} (I + H + H² + … + H^k-1)c exists and belongs to R (A* ). Therefore the Kaczmarz method converges for arbitrary A, b and x⁽⁰⁾ and

lim_{k® ¥} x^(k) = PN _(A)x⁽⁰⁾. + h, provides a description of the limiting vector provided by the method. Noting that h does not depend on x⁽⁰⁾, and that both c and h belong to R (A* ), h = Hh + c = [I - H|R _(A*)]^-1c.

Now, let us consider the case when Ax = b is consistent and x is a solution of it. Then, x lies on the intersection of all the m-hyperplanes so that x = Hx + c. Taking x as x⁽⁰⁾ we get x^(k) = x , for all k, and so x = PN _(A)x + h . Since h Î R (A* ) and PN _(A)x Î N (A), it follows that h is the minimum norm solution of Ax = b, and it is the limiting vector obtained by the Kaczmarz method after choosing x⁽⁰⁾ = 0. Finally, the solution of Ax = b nearest to a given vector z is obtained by minimizing P z - (y+h )P with respect to y Î N (A), it being the orthogonal projection of z on the solution space, and hence is given by PN _(A)[z - h ] + h = PN _(A)z + h , as h Î R (A^*). Since the vector PN _(A)z + h is the limiting vector provided by the Kaczmarz method using x⁽⁰⁾ = z , it follows that the Kaczmarz method for a consistent system converges to the solution of the system nearest to the starting vector x⁽⁰⁾. Summarizing, we have:

Theorem. The iterations {x^(k)}_{k³ 0} in the Kaczmarz method for Ax = b converge to the limiting vector x^{(¥ )} = lim_{k® ¥} x^(k) = PN _(A)x⁽⁰⁾. + h , where h does not depend on x⁽⁰⁾. If Ax = b is consistent h is the mininimum norm solution of it, and, moreover, x^{(¥ )} is the sloution of the system nearest to the initial vector x⁽⁰⁾.

The Method of Residual Projections

The analysis in the sequel shows that the sequence {x^(k)}_k³ 0 generated by the residual projection method converges to a vector x minimizing the residual b-Ax in the inner product space C^m with (y, z) = z* y and the norm P yP = (y* y)^1/2, note that y* here and in the sequel denotes the adjoint of y with respect to the inner product under consideration. Thus, if M deotes the positive definite matrix associated with an inner product on K ^m, z* y = (y, z) = (z¢ )^-My, so that z* º (z¢ )^-M. [Similarly for a linear functional Rx where R is a row vector, if N is the matrix associated with an inner product on K ⁿ, (x, R* ) = Rx = RN^-1Nx = ((N^-1(R')^-)¢ )^-Nx, so that R* = (N^-1(R')^-)].

Let A be an m´ n complex matrix with each column containing at least one nonzero entry, and b an m´ 1 vector. The j-th column vector of A is denoted by C_j. Let p_j = (C_j* C_j)^-1 and D_j = p_jC_j. With x⁽⁰⁾ as the initial vector we put

The residual projection algorithm generates a sequence {x^(k)}_k³ 0 of iterates in which the j-th component x^(k+1)_j of x^(k+1) is computed through

d _j^(k) = D_j* r^(k,j-1), x_j^(k+1) = x_j^(k) + d _j^(k), j = 1, 2, … , n,

r^(k,j) = r^(k,j-1) - d _j^(k)C_j, j = 1, 2, … , n,

Let P_j = p_jC_jC_j* , j = 1, 2, … , n, denote the orthogonal projection on the subspace <C_j> generated by the column vector C_j and put Q_j = I -P_j. Since

r^(k,j) = r^(k,j-1) - d _j^(k)C_j = (I-(C_j* C_j)^-1C_jC_j* )r^(k,j-1) = (I-P_j)r^(k,j-1) = Q_jr^(k,j-1) = Q_jQ_j-1… Q₁ r^(k,0) = Q_jQ_j-1… Q₁ r^(k),

r^(k+1) = Q_nQ_n-1 Q₂Q₁r^(k) = Hr^(k), k ³ 0,

and Q_j denotes the orthogonal projection on <C_j>^ , the orthogonal complement of <C_j>.

x_j^(k+1) = x_j^(k) + p_jC_j* r^(k,j-1) = x_j^(k) + p_jC_j* Q_j-1… Q₁ r^(k) = x_j^(k) + p_jC_j* Q_j-1… Q₁ [b - Ax^(k)].

say, where R denotes the matrix with j-th row vector equalling p_jC_j* Q_j-1… Q₁. Since K ^m = R (A) Å ^ N (A* ), for x Î K ^m, using x = P_Ax + PN _(A*)x = y + z, where y Î R (A) and z Î N (A* ), we have Q_jz = (I - (C_j* C_j) ^-1C_jC_j* )z = z, and Q_jy = (I - (C_j* C_j) ^-1 C_jC_j* )y Î R (A). Thus, R (A) and N (A* ) are invariant under each Q_j which is an identity operator on N (A* ). It follows that R (A) and N (A* ) are invariant under H, and that H is an identity operator on N (A* ).

We show that the restriction H|R _(A) of H to R (A) has norm less than 1. For this, since H = Q_nQ_{n-1 …} Q₂Q₁ and each Q_j is an orthogonal projection P HP £ 1 and so P H|R _(A)P £ 1.

Let y Î R (A) have P HyP = P yP . Then, Q_jy = y, 1£ j £ n, so that C_j* y = 0 for each j, implying that A* y = 0, i.e., y Î N (A* ). Hence y = 0. Hence for every 0 ¹ y Î R (A), P HyP < P yP , so that sup₀¹ yÎ R (A) P HyP /P yP being attained on the surface of the unit sphere in R (A), we have proved that

r º P H|_R(A)P < 1.

r^(k) = H^kr⁽⁰⁾ = (H|R _(A))^kPR _(A)r⁽⁰⁾ + PN _(A*)r⁽⁰⁾ ® PN _(A*)r⁽⁰⁾ = PN _(A*)b, k ® ¥ .

Note that P r^(k,j)P = P Q_jr^(k,j-1)P £ P r^(k,j-1)P , 1 £ j £ n, so that P r^(k+1)P = P r^(k,n)P £ P r^(k,0)P = P r^(k)P , so that the norms of the residuals constitute a monotone non-increasing sequence. Also,

d ^(k)_j C_j = [D_j* r^(k,j-1)]C_j = [p_jC_j* r^(k,j-1)]C_j = [p_jC_jC_j* r^(k,j-1)] = P_j r^(k,j-1) = P_jQ_j-1 r^(k,j-2) = …

d ^(k)_jC_j = P_jQ_j-1Q_j-2 … Q₁ r^(k) = P_jQ_j-1Q_j-2 … Q₁ [(H|R _(A))^kPR _(A)r⁽⁰⁾ + PN _(A*)r⁽⁰⁾] = P_jPN _(A*)r⁽⁰⁾ + P_jQ_j-1Q_j-2 … Q₁ [(H|R _(A))^kPR _(A)r⁽⁰⁾] = P_jQ_j-1Q_j-2 … Q₁ [(H|R _(A))^kPR _(A)r⁽⁰⁾].

It follows that P d ^(k)_jC_jP £ s ^kP r⁽⁰⁾P . Hence P d ^(k)_jP £ r ^kP r⁽⁰⁾P /P C_jP , so that

x^(k)_j = x^(k-1)_j + d ^(k-1)_j = x⁽⁰⁾_j + d ⁽⁰⁾_j + d ⁽¹⁾_j + … + d ^(k-1)_j ® x⁽¥ )_j = x⁽⁰⁾_j + S _k³ 0 d ^(k)_j, 1 £ j £ n,

the last series converging, it being dominated by the geometric series S _k³ 0 r ^kP r⁽⁰⁾P /P C_jP , in norm. Hence the method of residual projections converges. Since, P_Ab - Ax⁽¥ ) = P_A[b - Ax⁽¥ )] = P_A[PN _(A*)b] = 0, i.e., Ax⁽¥ ) = P_Ab, it follows that x⁽¥ ) is a least squares solution of Ax = b.