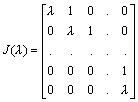Linear Transformations (Operators)

Let U and V be two vector spaces over the same field F. A map T from U to V is called a linear transformation (vector space homomorphism) or a linear operator if T(au₁ +bu₂) = aTu₁ + bTu₂ , a,b Î F , u₁, u₂ Î U. [In the sequel we will prefer the usage "operator" if U = V and "transformation" if U ¹ V. Moreover, unless otherwise specified, the symbol "T" would normally stand for a linear operator on a finite dimensional vector space V over a general field F.]

Given a linear transformation T : U ® V , if U is finite dimensional with dim U = n, and if B = {u₁, u₂, … , u_n} is an ordered basis of U , let Tu = v Î V. Then, if u Î U and [u]_B = (x₁, x₂, … , x_n)¢ , we have Tu = TB[u]_B = (Tu₁ | Tu₂ | … | Tu_n)(x₁, x₂, … , x_n)¢ = x₁Tu₁ + x₂Tu₂ + … + x_nTu_n = x₁v₁ + x₂v₂ + … + x_nv_n.

Conversely, if v₁, v₂, … , v_n Î V , B is a basis of U and for u Î U , if we define Tu = x₁v₁ + x₂v₂ + … + x_nv_n, where x = [u]_B , then T is a linear transformation from U to V. Thus every linear transformation T : U ® V is obtainable by picking up a basis B of U , defining T on B by assigning some elements of V to the elements of B and then extending T to the whole of U by linearity.

Let T : U _n ® V _m (n and m denoting the dimensions) be a linear transformation and U = B_U = {u₁, u₂, … , u_n}, V = B_V = {v₁, v₂, … , v_m} be two ordered bases of U and V , respectively. Let [Tu_j]_V = (a_1j, a_2j, … ,a_mj)¢ , j = 1, 2,... , n, denote the coordinate vectors of Tu_j with respect to the basis V = B_V of V. Then for a u Î U , Tu = T(U [u]_U) = (Tu₁ | Tu₂ | … | Tu_n)[u]_U = V A[u]_U ,where A = (a_ij) is an m´ n matrix. Thus [Tu]_V = A [u]_U and defining [T]_U,V = A, we have [Tu]_V = [T]_U,V [u]_U.

We call [T]_U,V as the matrix of T with respect to the ordered bases U = B_U and B_V of U and V , respectively. Dropping the subscript bases, we can rewrite the above result simply as [Tu] = [T][u].

It is worthwhile reiterating the construction of [T]: For T : U ® V , the (i, j)-th entry of A = [T] equals the scalar coefficient of the i-th element v_i of the basis V = B_V of V in the expression Tu = S _{1£ i£ m} a_ijv_i, for the vector Tu obtained by applying T to the j-th element u_j of the basis U = B_U of U. In other words, the j-th column of [T]_U,V is the coordinate vector [Tu_j ]_V.

If S and T are linear transformations from U to V and c is a scalar we can define T+S and cT by (T+S)u = Tu +Su, and, (cT)u = cTu. With this addition and scalar multiplication the set of all linear transformations form U to V , itself becomes a vector space and is denoted by L (U, V). Note also that [T+S] = [T] + [S] and that [cT] = c[T]. Further, if T : U ® V , and, S : V ® W are linear transformations, then the composition map ST is a linear transformation from U to W and that with rspect to any triple of ordered bases U , V, W of U, V, and W one has [ST]_U,W = [S]_V,W [T]_U,V. This is because STu = S(Tu) implies [ST][u] = [STu] = [S][Tu] = [S][T][u].

Theorem. Let U and V be, respectively, m and n dimensional vector spaces over a field F. Then for any two ordered bases of U and V , the map T ® [T] is a vector space isomorphism of L (U, V) onto F ^{m´ n}.

Proof: If A is an m´ n matrix, the map T defined by [Tu] = A[u], is a linear transformation from U to V. Hence T ® [T] is onto F ^{m´ n}. That the map is linear and is one to one is obvious. #

Using the above theorem, problems concerning linear operators on finite dimensional vector spaces can be posed equivalently as the related problems concerning ordinary matrices. The space L (V, V) is abbreviated by L (V) and if T Î L (V), [T]_B,B is written simply as [T]_B. It is easily verified that L(V) is an algebra (i.e., a vector space along with a binary multiplication which is associative, left and right distributive over the addition, and allows a free movement of scalar multiplication, viz., (aT)(bS) = ab(TS) over the field F of V. An operator T Î L (V) is called diagonalizable if there exists an ordered basis B of V such that [T]B is a diagonal matrix. If for some ordered basisB , [T]_B is upper (lower) triangular matrix, we call T a triangulable operator. The ordered basis B in such a case is referred to as a diagonalizing or a triangulizing basis, as the case may be.

For a given T Î L (V), a basis B = {v_i,i,v_1,2, … , v_1,p(1), v_2,1, v_2,2, … ,v_2,p(2), … , v_k,1, v_k,2, … , v_k,p(k)}, with p(1), p(2), … , p(k) ³ 1, of V is called a Jordan basis if there exist scalars l ₁, l ₂,... , l _k such that for 1 £ i £ k, Tv_i,1 = l _iv_i,1 , and Tv_i,j = l _iv_i,j + v_i,j-1, 1 < j £ p(i).It may be observed that the matrix of T with respect to such a Jordan Basis B is of the block diagonal form [T]B = diag (J₁, J₂, … , J_k), where for 1 £ i £ k, the i-th diagonal block is a Jordan block, which is a matrix of the type

.

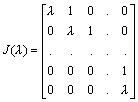of size p(i)´ p(i) with l = l_i, which for p(i) = 1 is simply the 1´ 1 matrix [l ].

It is clear that a Jordan basis is, in particular, a triangulizing basis. A matrix of the type diag (J₁(l ₁), J₂(l ₂), … , J_k(l _k)), where J_i(l _i) 's are Jordan blocks, is said to be of Jordan canonical form.

PROBLEMS

1. Let T be an idempotent operator (or projection, i.e., T² = T) of rank r on an n-dimensional vector space V. Prove that there exists a basis B of V s.t.

,

where I is an r´ r identity matrix.

2. Let q be a real number. By showing that one is the matrix of the other w.r.t. an appropriate basis, prove that the following matrices are similar over C:

.

3. If dim V ³ 2, prove that the algebra L (V) is non commutative.

4. Let B be a basis of an n-dimensional vector space V. Show that the map T ® [T]_B is an isomorphism (preserves all algebraic operations) between the algebras L(V) and F^{n´ n}.

5. The dimension of an algebra A over F is defined to be simply the dimension of A as a vector space over F. If dim V = n, what is the dimension of the algebra L(V)?

6. Prove that the dimension of the subspace of F^{5´ 5} consisting of matrices of type

,

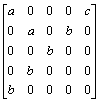where a, b, c Î F is 3. Prove also that no matrix of this type has rank 3, but that there are those of ranks 1, 2, 4 and 5.

7. Prove that the matrices of type

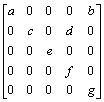
form a subalgebra of the algebra F ^{5´ 5}. Determine its dimension.

8. Prove that a set of linear operators L : U ® V , is l.i. iff the corresponding set of matrices [L]_U,V of them w.r.t. any ordered bases U and V of U and V are l.i.

9. Let T : F ⁿ ® F ^m be defined by T(X) = AX. Find conditions on A for T to be : (a) I (the identity operator); (b) 0 (the zero operator); (c) idempotent (i.e., T² = T); and (d) nilpotent (i.e., T^m = 0, for some m).

10. Let U and V be vector spaces over a field F. Let u_i Î U and v_i Î V , 1 £ i £ m. Show that there exist a linear transformation T from U into V such that Tu_i = v_i , 1 £ i £ m, iff S _{1£ i£ m} c_iv_i = 0, whenever c_i 's are scalars such that S_1£i£m c_iu_i = 0.

11. If T is a linear transformation from F⁽ⁿ⁾ into F^(m) , show that there exists an n´ m matrix B such that Tx = xB, x Î F⁽ⁿ⁾. Find B if Te_i = (y_i1, y_i2, … , y_im), where e_i Î F ⁽ⁿ⁾ denotes the row vector with i-th component 1 and all other components 0.

12. Let V be an n dimensional vector space and W an m dimensional vector space over a field F. Let T Î L (V, W). Show that: (a) if T is onto W , n ³ m; (b) if T is 1-1 from V into W , m ³ n; (c) if T is 1-1 onto from V to W , m = n; and (d) if n > m, N (T) ¹ {0}.

13. Describe explicitly all linear transformation from R ³ into R ³ whose range precisely consists of the subspace spanned by the vectors (1,1,1)¢ and (1,0,1)¢.

14. Let B Î V = F^{n´ n}. Define the transformations T, S : V ® V by T(A) = AB-BA+BAB, and S(A) = AB-BA+ABA, A Î V. Show that T is a linear transformation from V into V. When will S be a linear transformation form V into V. Is it so iff S = 0?

15. Find a real linear functional f on C (i.e., f Î (C (R))* which is not complex linear (i.e., f Ï (C (C))*).

16. Let C ⁿ(R) denote the vector space of n-component complex column vectors over the field R. Use matrices to explicitly describe the most general linear transformation from U to V when: (a) U = C ⁿ(R), V = C ^m(R); (b) U = C ⁿ(R), V = R ^m; (c) U = R ⁿ, V = C ^m(R); (d) U = C ⁿ, V = C ^m; and, (e) U = R ⁿ, V = R ^m.

17. Let T : F ^{m´ n} ® F ^{m´ n} be defined by T(B) = ABC, where A Î F ^{m´ m} and C Î F ^{n´ n}. Find necessary and sufficient conditions on A and B for T to be the zero operator.

18. Find necessary and sufficient conditions for T : F ^{m´ n} ® F ^{m´ n} defined by T(B) = ABC, (A Î F ^{m´ m}, C Î F ^{n´ n}) to equal I.

19. Let V be an n-dimensional vector space over F. Prove that there exists a T Î L (V) such that R (T) = N (T) iff n is even. If n = 2m, give an example of such a T.

20. Prove that T Î L (V) satisfies R (T) = N (T) iff there exists a basis B of V such that for some invertible A,

.

21. If V is a finite dimensional vector space and T Î L (V), show that the following statements about T are equivalent : (a) R (T) Ç N (T) = {0}; (b) N (T²) = N (T); and (c) there exists an invertible A, and a basis B of V such that

.

22. For what polynomials h over F is the mapping h :f ® f(h) a one-one linear transformation from F [x] onto F [x].

23. If T is a linear operator on F ⁿ and A is the matrix of T in the standard ordered basis for F ⁿ, what is the relationship between R (T) and R (A)?

24. If V is a vector space over a field F , B is an ordered basis for V , T Î L (V) and

[T]B = ,

prove that: (a) T² -(a+d)T+(ad-bc)I = 0; (b) T is a scalar operator iff a = d and b = c = 0; (c) T is not a scalar operator iff T² +a T+b I = 0 implies that a = -(a+d) and b = ad-bc.

25. Let T be the linear operator on R ³, the matrix of which in the standard ordered basis is

.

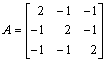Find a basis for R (T) and another for N (T).

26. Show that the matrices and are similar.

27. Show that B = {(1,-i)',(-i,1)'} is a basis of C ². Find the matrices of the linear operators on C ² with respect to B , whose matrices with respect to the standard ordered basis of C ^{2´ 2} are

,

where q is any complex number. Are these matrices similar? Is any of them similar to matrix diag (e^iq ,e^-iq)?

28. If T is a linear operator on a two dimensional vector space V such that T² = T, prove that T = 0, or, T = I, or there exists an ordered basis B for V such that [T]_B = diag (0, 1).

29. If V is n-dimensional with a basis V = {v₁, … , v_n} and W is m-dimensional with a basis W ={w₁, … , w_n} and if [T]_V,W = A, show that the operator T Î L(V , W), is given by T = S _{1£ i£ m} S _{1£ j£ n} a_ij w_i Ä v_j¢ , where V ¢ ¢ = {v_1¢ , … ,v_n¢ } is the dual basis of V ¢ and the tensor product is defined by (w_i Ä v_j¢)(a) = v_j¢(a)w_i.

30. Let Q be the rational field and f a polynomial over Q. Let A in Q ^{2´ 2} be given by

(a) Show that f(A) is singular iff f(A) = 0. (b) Compute f(A) if f(x) = x² -5x -2. (c) Compute f(A) if f(x) = x⁴ -5x² -2. (d) Compute f(A) if f(x) = x¹⁰ (x-5)¹⁰. (e) Determine a strategy to compute A¹⁰⁰, say.

31. Let T be the linear operator on R³ defined by T(x₁, x₂, x₃) = (x₃, x₁, x₂). Compute f(T) if: (a) f(x) = x²; (b) f(x) = x³; (c) f(x) = x¹⁰⁰⁰.

32. Let A = diag (d₁, d₂, … , d_n). Compute the matrix f(A) if: (a) f(x) = (x-d₁)(x-d₂) … (x-d_n); (b) f(x) = x¹⁰⁰; (c) f(x) = (x+1)¹⁰⁰.

33. Compute A⁴⁸ and A⁴⁹ if A is the 50´ 50 matrix, with

34. Let V = C over R and W = R^{2´ 2} over R. Note that V and W are algebras with the usual multiplication. If T is a non-trivial algebra homomorphism from V into W , i.e., T Î L(V ,W) and satisfies T(z₁ z₂) = T(z₁)T(z₂), z₁, z₂ Î C , and T is non-zero, show that : (a) T is invertible; (b) det (Tz) = |z|² ; and, (c) there exist g , d Î R , with g ¹ 0, such that

35. Consider C as a vector space V over R (i.e., V = C (R)). What is the dimension of L(V)? What is the dimension of L(R ²)? Can L(V) and L(R ²) be identified? Identify the members of L(C ¹)\L(V) (complex linear but not real linear), L(V)\L(C ¹) (real linear but not complex linear) and L(C ¹)Ç L(V) (both real and complex linear). (Note that R ² = R ²(R), C ¹ = C ¹(C)).

36. What is the matrix of the transformation T : F ^{m´ n} ® F ^{m´ n} defined by TX = AX, with respect to the standard basis {{E_ij, 1 £ j £ n}, 1 £ i £ m}, where A Î F ^{m´ m}? When is T: (i) identity, (ii) zero, (iii) singular, and (iv) invertible? Are f_T and f_A, and p_T and p_A related? Find the relationship.

37. Let T be a linear transformation over an n-dimensional vector space V. Prove that R (T) = N (T) iff there exist a _j Î V , 1 £ j £ m, such that B = {a₁, a₂, … , a_m, Ta₁, Ta₂, … , Ta_m} is a basis of V and that T² = 0. Deduce that V is even dimensional.

38. Let T be a linear transformation over an n-dimensional vector space V. Prove that R(T) Ç N(T) = {0} iff whenever G is a basis of N (T) and R is a basis of R (T) then G È R is a basis of V.

Change Of Bases

Let dim V = n, g = {v₁, v₂, … , v_n} and b be two ordered bases of V , T Î L(V) º L(V, V), and write [T]_b,b simply as [T]b. We have v = b[v]_b = g[v]_g = b[g ]_b[v]g for every v Î V. It follows that

[v]_b = [g ]_b [v]_g ,

and that similarly, [v]_g = [b]_g [v]_b. Hence, for any v Î V , [v]_b = [g ]_b [b ]_g [v]_b , so that [g ]_b [b]_g = I. i.e.,

[g ]_b = [b]_g ^-1, [b]_g = [g]_b ^-1.

Now, Tv = b [T]_b [v]_b = g [T]_g [v]_g = b [g ]_b [T]_g [b]_g [v]_b , so that [T]_b = [g ]_b [T]_g [b ]_g = [b]_g ^-1[T]_g [b]_g. Interchanging the roles of b and g , we have

[T]_g = [b ]_g [T]_b [g ]_b = [g ]_b^-1[T]_b [g ]_b.

In particular, if V = F ⁿ, and T = A, an n´ n matrix, with

C = 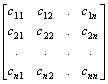= [c₁ | c₂ | … | c_n] = b ,

and g = [e₁ | e₂ | … | e_n] = I, e_i’s being the standard unit vectors, then

[T]b = [A]_C = C^-1AC.

In the case of a linear transformation T : V ® W , let a , b be bases of V and g , d those of W. Let v Î V. Then, Tv = d [Tv]_d = d [T]_b,d [v]_b. Hence g [T]_a,g [v]_a = g [d ]_g [T]_b,d [a]_b[v]_a so that [T]_a,g = [d ]_g [T]_b,d [a]_b.

In particular, if b , g were standard bases in F ⁿ and F ^m and T = A (m´ n) : F ⁿ ® F ^m, and a = P, g = Q, then

[A]_a,g = [A]_P,Q = Q^-1AP, [x]_P = P^-1x, &, [y]_Q = Q^-1y.

Finally, suppose T : U ® V , and S : V ® W and a , b , and g are ordered bases in U , V , and W , respectively. Then g [ST]_a,g [u]_a = STu = S(Tu) = g [S]_b,g [T]_a,b [u]_a , so that

[ST]_a,g = [S]_b,g [T]_a,b.

Theorem. Let T be a linear operator on V and b an ordered basis of V. Then T is triangulable (diagonalizable) iff the matrix [T]_b is triangulable (diagonalizable).

Proof: Let b = {v₁, v₂, … , v_n} and C Î F ⁿ´ n be invertible. Let {w₁, w₂, … , w_n} = g = b C º {S ₁£ i£ n c_ijv_i}₁£ j£ n. Then [T]_g = [g ]_b^-1[T]_b [g]_b = C^-1[T]_bC is triangular (diagonal) iff C triangulizes (diagonalizes) [T]. #

PROBLEMS

1. Let T, S Î L(V), V finite dimensional. Show that there exists an invertible R Î L(V) such that R^-1TR = S iff for some ordered bases b , g of V , [T]_b = [S]_g.

2. Let V and W be finite dimensional vector spaces with the respective bases b = {v₁, v₂, … , v_n} and g = {w₁, w₂, … , w_m}. Let T Î L(V), S Î L(V , W) and R Î L(W) and [T]_b = A, [S]_b,g = B and [R]_g = C. If a = {v_n, v_n-1, … , v₁}, and d = {w_m, w_m-1, … , w₁}, compute [T]_a, [T]_b,a, [T]_a,b, [S]_b,g, [S]_a,g, [S]_a,d, [R]_d, [R]_g,d, [R]_d,g, [RST]_b,d, [RS]_a,d, and [ST]_a,d given that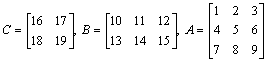

.

3. Consider V = R² regarded as the standard plane with the x- and the y- axes so that a point P(x, y) corresponds to the column vector (x, y)'. Show that the operations of finding: (a) the feet of perpendiculars of P on the axes, (b) reflection of P in the axes, (c) reflection of P in the origin, correspond to linear operators on V , and find the matrices of these in the standard ordered basis.

4. Find a geometrical interpretation of the action of the linear operators on R³ the matrices of which with respect to the standard ordered basis in R are given by

5. Consider the succession of the following operations on a point P in R ³ performed one after the other: (i) reflect in the yz-plane, (ii) take perpendicular projection on the xy-plane, (iii) rotate the point about the y-axis till the positive direction of the x-axis coincides with that of the z-axix, and, finally, (iv) take the perpendicular projection of the point on the x-axis. Model each operation as the action of a matrix on a vector to determine as to what happens to the point in the end?

6. Let T be the linear operator on C ³, for which Te₁ = (1, 0, i)¢ , Te₂ = (0, 1, i)¢ , Te₃ = (i, 0, 1)¢. Is T invertible?

7. Let T be the linear operator on C defined by T(x₁, x₂, x₃)¢ = (3x₁+x₃, 2x₁+x₂,x₁+x₂+x₃)¢. Show that T is invertible and find a rule for T^-1 like the one which defines T. Find real a, b, c, d such that T = aI + bT +cT² and hence express T³ as a linear combination of I, T, and T².

8. Let C ²´ 2 be the complex vector space of 2x2 matrices with complex entries. Let

and let T be the linear operator on C ²´ 2 defined by T(A) = AB. What is the rank of T? If P is a polynomial, do: P(T)A = P(B)A, and, P(T(A)) = P(T)A, hold?

9. Let T be a linear transformation from R ² into R , and U from R into R ². Prove that UT is not invertible. Generalize.

10. Find linear operators T and S on R , if possible, such that: (a) ST ¹ 0 and TS = 0; (b) T² = 0 = S², and 0 ¹ TS ¹ ST ¹ 0. Also show that T² = 0 iff R (T) Ì N (T).

11. If T : V ® W is a linear operator, verify that the following statements are equivalent: (a) T is invertible; (b) T is 1-1 onto; (c) T is an isomorphism of V and W (V onto W); (d) there exists a linear operator S : W ® V such that TS = I on W and ST = I on V.

12. Let T : V ® W be a linear operator. Show that if any of the following hold then T is not invertible: (a) dim V < dim W ; (b) dim V > dim W ; (c) for some S Î L(W , V), ST = I but S is not invertible; (d) for some S Î L(W, V), TS = I but S is not invertible; (e) for some S Î L(W, V), TS = I but ST ¹ I; (f) for some S Î L(W, V), ST = I but TS ¹ I; (g) for some S : W ® V , TS = I but S is not linear; and (h) for some S : W ® V , ST = I but S is not linear. Give an example of each type.

13. Give an example of a T Î L(V , W) of each of the following types: (a) T is not 1-1; (b) T is not onto; (c) N (T) ¹ {0}; (d) Tv = w does not have a solution for all w but that whenever it does the solution is unique; and (e) Tv = w has a solution for all w but that the solution is not unique for a single w. The examples should cover both finite and infinite dimensional spaces and the cases when V ¹ W , as well as when V = W. In which of these cases is T invertible?

14. If T Î L(V , W) an operator S : W ® V is called an inverse of T if ST = I and TS = I. Such an S is denoted by T^-1. Prove that if such a T exists, it is unique and linear. Verify that T has an inverse iff T is invertible.

15. Prove that T^-1 is invertible and (T^-1)^-1 = T. If T and S are invertible linear operators on a finite diemensional vector space, prove that (T+S)^-1 exists and equals T^-1 + S^-1 iff S = W T, where I + W + W ² = 0.

16. If T and S are linear operators on a finite-dimensional space V such that TS = I, prove that ST = I, that both T and S are invertible and that S = T^-1 and T = S^-1. Is the result true if V is infinite dimensional?

17. T Î L(V , W) is called singular if for some v ¹ 0, Tv = 0. If T is not singular it is called nonsingular. If V and W are finite dimensional, prove the equivalence of: (a) T is invertible; (b) T is non-singular; (c) T^-1 exists; (d) Tv = w has a solution for each w Î R (T); (e) Tv = w does not have two distinct solutions; and (f) Tv = 0 implies that v = 0.

18. Let V be a finite-dimensional vector space and let T Î L(V). Let S denote the restriction of T to R (T). Prove that S is invertible iff rank (T²) = rank (T).

19. Let V be a finite dimensional vector space. Let T Î L(V) and R Î L(L(V)) be defined by R(S) = TS, S Î L(V). Which of the following statements are true: (a) R is invertible iff T has a left inverse (a Q such that QT = I); (b) R is invertible iff T has a right inverse (a Q such that TQ = I); (b) (a) R is invertible iff T has an inverse (a Q such that QT = I and TQ = I). Answer the same question if V is infinite dimensional.

20. Let T be the linear transformation from R³ into R² defined by T(x₁, x₂, x₃)¢ = (x₁+x₂+x₃,x₁-2x₂+x₃)¢. Find the matrix of T relative to the standard ordered bases of R³ and R². What is the matrix of T relative to B = {u₁, u₂, u₃} and G = {v₁, v₂}, when u₁ = (1, 0, -1)¢ , u₂ = (1, 1, 1)¢ , u₃ = (1, -2, 1)¢ , v₁ = (-1, 1)¢ , and v₂ = (1, 1)¢ ?

21. Let b > a > 0 and T on R ² be defined by T(x₁, x₂)¢ = (ax₁-bx₂, bx₁-ax₂)¢. (a) What is the matrix of T in the standard ordered basis for R²? (b) Find [T]b if b = {v₁, v₂}, where v₁ = (a, b)¢ and v₂ = (-b, a)¢ ? (c) Prove that for every c Î R , the operator (T-cI) is invertible. (d) If [T]g = A, prove that a₁₂a₂₁ ¹ 0, for any ordered basis g. (e) Interpret (d) using the notion of triangulability of T.

22. Let T be the linear operator on R³ defined by T(x₁, x₂, x₃)¢ = (2x₁+x₂+x₃, x₁+2x₂+x₃, x₁+x₂+2x₃)¢. (a) Prove that T is invertible and express T^-1 in a similar form. (b) What is the matrix of T in the standard ordered basis for R ³? (c) What is the matrix of T in the ordered basis {v₁, v₂, v₃}, where v₁ = (1, 1, 1)¢ , v₂ = (1, 1, -1)¢ , and v₃ = (1, -1, 1)¢ ? (d) What is the matrix of T in the ordered basis {w₁, w₂, w₃}, where w₁ = (1, 1, 1), w₂ = (1, -1, 0), and w₃ = (1, 0, -1)¢ ? (e) What is the matrix of T^m in the ordered basis {w₁, w₂, w₃}? (f) What is the matrix of T in the ordered basis {v₁, v₂, v₃}? (e) What is the matrix of T in the standard ordered basis for R³ ?

23. Let W be the space of all 1´ n row matrices over a field F. If A is an n´ n matrix over F , define a linear operator R_A on W as the right multiplication: R_A x = xA, x Î W. Prove that every linear operator T on W is the right multiplication by some n´ n matrix A. If T₁, T₂, … , T_m denote the right multiplications by the matrices A₁, A₂, … , A_m, show that their product T₁T₂ … T_m is the right multiplication by A_mA_m-1 … A₁, and not by A₁A₂ … A_m. Deduce that A is not the matrix of T_A in any basis b of W. What is the matrix of T_A in the standard ordered basis {e₁, … , e_n} of W given by e₁ = (1, 0, … , 0), … , e_n = (0, 0,... , 1)?

24. Let V be an n-dimensional vector space over a field F , and let b = {v₁, … , v_n} be an ordered basis for V. If T is a linear operator on V such that Tv_j = v_j+1, j = 1,... , n-1, and Tv_n = 0. Show that the matrix of T in the ordered basis b is similar to any n´ n matrix A which satisfies Aⁿ = 0, but A^n-1 ¹ 0, and conversely.

25. Let V be an n-dimensional vector space over the field F , and let b = {v₁, … , v_n} be an ordered basis for V. If T is a linear operator on V such that Tv_j = v_j+1, j = 1,... , n-1, and Tv_n = c₁v₁ + c₂v₂ + … + c_nv_n, show that the matrix of T in the ordered basis b is similar to an n´ n matrix A iff p_A (x) = xⁿ - (c₁ + c₂x +... + c_nx^n-1).

26. If F is a field of characteristic zero, and the indefinite integral operator J and the differential operator D on F [x] are as J = S ₀£ i£ n c_ixⁱ = S ₀£ i£ n (i+1)^-1c_ixⁱ⁺¹, and D S ₀£ i£ n c_ixⁱ = S ₁£ i£ n ic_ix^i-1, show that: (a) J is the unique solution of the operator equation: DJ= I, satisfying (Jp)(0) = 0 for all p Î F [x]; (b) D is the unique solution of the operator equation: JD = I-I₀, where I₀p = p(0), p Î F [x]; (c) J is not invertible but that it is non-singular; (d) D is singular and not invertible; (e) J has no eigenvector and D has only one eigenvalue and it is of geometric multiplicity 1; (f) Dⁿ(pq) = S ₀£ j£ n ⁿc_jDⁱp (D^n-jq), n ³ 0; (g) J(pq) = p(Jq) - J((Dp)(Jq)); (h) If deg(p) = n, J(pq) = S ₀£ k£ n (-1)^k-1(D^kp)(J^k+1q); (i) No finite dimensional subspace of F [x] is J-invariant; and (j) The only D-invariant subspace W of F [x] of dimension n is the subspace W = <1, x, x², … , x^n-1>, n ³ 1.