Chapter 5
SECOND ORDER FORMS
Bilenear and Multilinear Expressions on Product Spaces
Consider x, h Î R n, y, k Î R m and a function f : R n´ R m ® R . Under the assumption that f has continuous second order partial derivatives with respect to the components in x and y, we have
f(x+h, y+k) - f(x, y) = S 1£ i£ n hi¶ f/¶ xi + S 1£ i£ m ki¶ f/¶ yi + ½S 1£ i£ n S 1£ j£ m hihj¶ 2f/¶ xi¶ xj.+ ½S 1£ i£ m S 1£ j£ m kikj¶ 2f/¶ yi¶ yj + S 1£ i£ m S 1£ j£ n kihj¶2f/¶yi¶xj + o(P hP 2 + P kP 2),
in which the first sum on the right hand side is a linear expressions in h, the second is linear in k, the third is a quadratic in h, and, the fourth a quadratic in y. The fifth term is bilinear in h and k, i.e., it is linear both in h as well as k and is the dominant most mixed expression in h and k. An expression of the form B(x, y) = S 1£ i£ m S 1£ j£ n aijyixj = y¢ Ax, (x Î F n, y Î F m) is a bilinear-expression in the two vector variables x and y and it is a homogeneous polynomial of total degree 2 in xj 's and yi 's, and is linear with respect to both x and y, i.e., B(ax+bz, y) = aB(x, y) + bB(z, y), and B(x, ay+bt) = aB(x, y) + bB(x, t), for all x, z Î Fn, y, t Î Fm, and, a, b Î F. Conversely, if B(x, y) is linear both with respect to x Î F n and y Î F m, one easily sees that B(x, y) = y¢ Ax, for some A Î F m´ n.
More generally, a bilinear expression on a cartesian product V ´ W , V and W being vector spaces over a field F , is a function B : V ´ W ® F , which is linear with respect to both the arguments. If V and W are finite dimensional, b = {v1, , vn} is an ordered basis of V and g = {w1, , wm} that of W , writing x = [v]b and y = [w]g , B(v, w) = B(S1£ j£ n xjvj , S 1£ i£ m yiwi ) = S1£ j£ n xjB(vj, S 1£ i£ m yiwi) = S1£ j£ n S1£ i£ m xjyi B(vj, wi) = S1£ i£ m S1£ j£ n aijxjyi = y¢ Ax, where aij = B(vj, wi), 1 £ i £ m, 1 £ j £ n. Thus, naming A as the matrix [B]b g of B in the ordered bases V and W: B(v, w) = [w]g ¢ [B]b g [v]b .
On the other hand, if A Î Fm´ n, B(v, w) = [w]g ¢ A[v]b is a bilinear expression on V´W, so that the set B of all bilinear expressions on V´W is a vector space (with addition and scalar multiplication as of functions) isomorphic to the space F .
B(v, w) could be written more explicitly in terms of v, w as follows. Let f = {f1, f2, , fn} denote the basis dual to V and let j = {g1, g2, , gm} that dual to W. Then, since fj(v) = xj and gi(w) = yi, we have B(v, w) = S1£ j£ n S1£ i£ m B(vj, wi)fj(v)gi(w).
A multilinear expression on the cartesian product V1´V2´ ´Vk of vector spaces V1, V2, , Vk over a field F, is a function M : V1´V2´ ´Vk ® F, which is linear in each of its k-arguments. If each Vi is finite dimensional and b i = {vij : 1 £ j £ ni} is an ordered basis of Vi, it follows from the definition that M(v1, , vk) = S1£ j1£ n1 ... S1£ jk£ nk M(v1j1 , ... , vkjk ) x1j1 xkjk , where xij denotes the j-th cordinate of vi in the basis b i, 1 £ i £ k.
PROBLEMS
1. Let the bilinear expressions B(x, y) = y¢ Ax and H(x, y) = y¢ Gx on Fn´Fm satisfy B(x, y) = H(x, y) for all x, y. Show that A = H.
2. Show that a multilinear expression on Fp´Fq´ ´Fs is precisely of the form M(x, y, ... , t) = S1£ i£ p S1£ j£ q S1£ l£ s aij l xiyj tl.
3. Let V1 , V2 , , Vk be finite dimensional vector spaces over a field F, with ordered bases b 1, b 2, , b k and the respective dual bases f 1, f 2, , f k. Using these describe a multilinear expression M(v1, v2, , vk) on V1´V2 ´ ´ Vk , explicitly in terms of the vectors v1, v2, , vk.
4. If V and W are finite dimensional vector spaces and B(v, w) is a non-zero bilinear expression on V´W, show that there exists a positive integer k and ordered bases b and g of V and W such that if x = [v]b and y = [w]g then B(v, w) = S1£ i£ k xiyi, v Î V, w Î W. This result could be restated as
[B]
b g =5. If V and W are finite dimensional vector spaces over a field F, the rank of a bilinear expression B(v, w) on V´W is defined to be the rank of a representing matrix [B]b g , where b and g are any two ordered bases of V and W, respectively. Show that the rank of B does not depend on the particular choice of the bases b and g .
6. Let V and W be finite dimensional vector spaces over F. A bilinear expressions B(v, w) on V´W defines two transformations LB : V ® W¢ and RB : W ® V¢ by (Lv)(w) = B(v, w) = (Rw)(v). Show that L and R are linear and r(LB) = r(RB) = r(B), the rank of B.
7. If V and W are both n-dimensional and B(v, w) is a bilinear expression on V´W, such that r(B) = n, show that we can choose the bases b and g such that [B]b g = I. Then if T Î L(V), show that there is a unique S Î L(W) such that B(Tv, w) = B(v, Sw) and moreover that [T]b = [S]g ¢ so that tr [T]b = tr [S]g .
8. Let x, h Î R n, y, k Î R m and a function f : R n´ R m ® R , have continuous second order partial derivatives with respect to the components in x and y. Prove that
B(h, k) = limt® 0 t-2{f(x+th, y+tk) [f(x, y) + S 1£ i£ n thi¶ f/¶ x + S 1£ i£ m tki¶ f/¶ yi
+ ½S 1£ i£ n S 1£ j£ m t2hihj¶ 2f/¶ xi¶ xj + ½S 1£ i£ m S 1£ j£ m t2kikj¶ 2f/¶ yi¶ yj]},
exists and defines a bilinear expression on R n´ R m.
Bilinear forms on a Vector Space
If A Î Fn´ n the bilinear expressions y¢ Ax, x, y Î Fn is called a bilinear form on Fn and, more generally, a bilinear expression B(u, v) on V´V, is called a bilinear form on V. We denote the set of all bilinear forms on V by B(V, F). Choosing a common basis b (W = V) for both the arguments u and v, the matrix [B]b b of B(u, v) in the ordered basis b may simply be written as [B]b so that we have B(u, v) = [v]b ¢ [B]b [u]b . In this case of a bilinear form on a vector space V, a linear operator T Î L(V) is said to preserve a bilinear form B if B(Tu, Tv) = B(u, v). In terms of the matrices of B and T we have [T]b ¢ [B]b [T]b = [B]b ; the set of such non-singular T Î L(V) preserving B(u, v) is a subgroup of the group of non-singular operators under the usual product of operators in the algebra L(V), the identity operator is the identity and T-1 is the inverse of T in this subgroup.
Defining the scalar multiplication and addition for bilinear forms by: (cB)(u, v) = cB(u, v) and (B+E)( u, v) = B(u, v)+E(u, v), it follows that B(V, F) is a vector space over F. Moreover, if V is of dimension n, B(V, F) as a vector space is isomorphic to F n´ n, with an isomorphism given by h : B ® [B]b , where b is any basis of V. As Fn´ n is isomorphic to L(V), it follows that B(V, F) is isomorphic to L(V). In a certain sense there is a greater freedom in the study of matrices or linear operators via a bilinear form, e.g., one could consider the restriction of a bilinear form to an arbitrary subspace, whereas the restriction of an operator is not meaningful unless the subspace is an invariant one.
PROBLEMS
1. Find the matrices of the bilinear form B(x, y) = x1y2 x2y1, (x, y Î R2) with respect to the ordered bases b = {(0, 1)¢ , (1, 0)¢ } and g = {(2, 3)¢ , (3, 2)¢ }.
2. Find the matrix, in the standard ordered basis, of the bilinear form f(x, y) = ax1y1 + bx1y2 + cx2y1 + dx2y2, on R2. Find conditions on a, b, c, and, d so that f has rank: (i) 0; (ii) 1; and, (iii) 2. Show that f is non-degenerate iff (b+c)2 ¹ 4ad.
3. A bilinear form B(u, v) on a finite dimensional vector space V is called degenerate or singular if [B]b is singular for some ordered basis b of V. Show that the degeneracy or non-degeneracy of B(u, v) is independent of the choice of the particular basis b .
4. Prove that the bilinear form f(A, B) = n´ tr(AB) - tr(A)´ tr(B) on Fn´ n, n ³ 1, is degenerate, but that the restriction of f to the subspace W of matrices of trace zero is non-degenerate, if n > 1 and ch (F) n. More generally, show that
r(f) = ![]()
5. Show that the restriction of f(A, B) = n´ tr(AB) - tr(A)´ tr(B) on Rn to the subspace S of skew-symmtric matrices has the property that f(A, A) < 0, A ¹ 0.
6. If f(A, B) = n´ tr (AB) - tr (A)´ tr (B) and W is the subspace of F of all A such that f(A, B) = 0 for all B Î Fn´ n, show that: (a) W = {cI : c Î F} and dim W = 1, if ch F n; (b) W = {A : tr A = 0} and dim W = n -1, if ch F | n.
7. If f(u, v) is a bilinear form on a finite-dimensional vector space V and W is the subspace of all w such that f(w, v) = 0 for every v, prove that rank f = dim V - dim W.
8. Let f be a bilinear form on a finite-dimensional vector space V. If W is a subspace of V and g is the restriction of f to W prove that rank f ³ rank g.9. If f and g are bilinear forms on Fn and g is non-degenerate, show that f(x, y) = g(Ex, y) = g(x, Fy), x, y Î F , where E, F Î F are unique and similar. Is the result true if g is singular?
10. If V is a finite dimensional vector space, show that bilinear forms on V of rank 1 are precisely of the form f(a, b) = g(a)h(b), where 0 ¹ g, h Î V¢ .
11. Given a bilinear form B(u, v) on a finite-dimensional vector space V, for any subspace W of V, define WBl = {u Î V : B(u, w) = 0, w Î W}, WBr = {v Î V : B(w, v) = 0, w Î W}. Let WB^ commonly denote any one of WBl or WBr and let BW denote the restriction of B(u, v) to W. Show that: (a) WB^ is a subspace; (b) V = {0}B^ ; (c) VB^ = {0} iff B is non-degenerate; (d) r(B) = dim V - dim VB^ ; (e) dim WB^ ³ dim V - dim W; (f) the restriction BW is non-degenerate iff WÇ WB^ = {0}; (g) V = WÅ WB^ iff the restriction BW is non-degenerate.
12. If B(u, v) is a bilinear form on an n-dimensional vector space V and b = {v1, v2, , vn} and g = {w1, w2, , wn} are two ordered subsets of V such that u = S1£ i£ n B(u, wi)vi, u Î V, prove that: (i) B is non-degenerate, (ii) V and W are bases in V and (iii) there holds u = S1£ i£ n B(vi, u)wi , u Î V. Also, prove that given any non-degenerate B and an ordered basis b , a basis g with the above properties exists and is unique.
13. If B is a bilinear form on an n-dimensional vector space V, b = {v1, v2, , vn}, g ={w1, w2, , wn} are two ordered bases of V such that B(vi, wj) = d ij, 1 £ i, j £ n, show that if [B]b = A and C = A-1, wj = S1£ i£ n cijvi, 1 £ j £ n. Obtain a similar expression for vi 's in terms of wj 's and show that for a pair T, S Î L(V) such that B(Tu, v) = B(u, Sv), u, v Î V, [T]b ¢ = [S]g , and that tr (T) = tr (S) = S 1£ k£ n B(Tuk, vk) = S 1£ k£ n B(uk, Svk)S B(a , Sb ).
14. Let b = {v1, v2, , vn}, g ={w1, w2, , wn} be two bases of Fn and P and Q matrices with the respective i-th column vectors as vi and wi, 1 £ i £ n. If A is the matrix of a bilinear form B(u, v) on Fn, in its standard basis, and B(vi, wj) = d ij, 1 £ i, j £ n, prove that Q = (P¢ )-1(A¢ )-1.
15. Show that B(X, Y) = trace (XtAY), X, Y Î Fm´ n, where A is a fixed n´n matrix, is a bilinear form on V = Fm´ n. Find the matrix of B with respect to the standard ordered basis of Fm´ n given by b = {E11, , E1n, E21, , E2n, , Em1, , Emn}, where Epq has its (p, q)-th entry as 1 and the rest zero.
16. Find the matrix of the bilinear form B(x, y) = y¢ x on Kn with respect to the ordered basis consisting of the columns of a member of O(n, K), the group of n´n orthogonal matrices M over K, which are the non-singular matrices whose transposes are their inverses.
17. If the matrix of a bilinear form on a finite dimensional vector space is independent of the choice of the basis, what can you say about the bilinear form?
18. Show that the bilinear form B(x, y) = y¢ Ax on Kn, is invariant under O(n, K) iff A commutes with each member of O(n, K).
19. If T is a linear operator on a finite dimensional vector space V, preserving a bilinear form B on V, show that det T = ± 1.
20. Prove that a matrix operator C preserves a non-degenerate Fn bilinear form B(x, y) = y¢ Ax iff A-1C¢ A = C-1.
21. If B is a bilinear form on a finite-dimensional vector space V, T is an invertible linear operator on V and if BT is the bilinear form on V given by BT(u, v) = B(Tu, Tv), show that a linear operator U on V preserves BT iff the operator TUT-1 preserves B.
22. If M Î F2´ 2, for the the bilinear form B(x, y) = x1y2 x2y1 on F2, verify that B(Mx, My) = |M|B(x, y) and deduce that M¢ AM = A, where
A = ![]() ,
,
iff |M| = 1, i.e., M is unimodular.
23. If A, B, C, D, I Î Fn´ n, I being the identity matrix and
M = ![]() , J =
, J = ![]() ,
,
show that M¢ JM = J iff A¢ C is symmetric and A¢ D - C¢ B = I.
24. Show that B(x, y) is a bilinear forms on Kn invariant under O(n, K) iff B(x, y) = cS1£ i£ n xiyi, where c Î K is a scalar.
25. Let f be a bilinear form on a finite dimensional vector space V over K. If f is non-singular show that any basis b of V can be ordered so that the matrix A of f in the ordered basis b has all its principal minors different from 0 and that there is a unique upper-triangular matrix U with diagonal entries 1 such that U* AU is upper-triangular. Is the result true for a general field with U* replaced by U¢ ?
Symmetric and Skew-Symmetric Bilinear Forms
Since a bilinear form B(u, v) is a bilinear expression on the cartesian product of a vector space with itself, in this case there arises the possibility of interchanging the areguments in B(u, v) and thus of comparing B(u, v) with B(v, u). Accordingly, a bilinear form B(u, v) on V is called symmetric if B(u, v) = B(v, u) and anti-symmetric or skew-symmetric if B(u, v) = -B(v, u) for all u, v Î V. Clearly, the set S(V, F) of all symmetric bilinear forms on V, as well as the set S~(V, F) of all skew-symmetric bilinear forms on V are subspaces of B(V, F). Passing to the matrices with respect to any ordered basis b of V it follows that the form B(u, v) is symmetric iff [B]b is symmetric; and the form B(u, v) skew-symmetric iff [B]b is skew symmetric. If ch (F) ¹ 2, we have B(u, v) = [B(u, v)+B(v, u)]/2 + [B(u, v)-B(v, u)]/2, from which it follows that any bilinear form on V over a field of characteristic different from two can be written as a sum of a symmetric bilinear form and another skew-symmetric bilinear form. On the other hand, in a field of characteristic 2, the two notions of symmetric and skew-symmetric bilinear forms coincide, i.e., B(u, v) is symmetric iff it is skew-symmetric. Thus, for example the bilinear form B(x, y) = x1y2, x, y Î Z 22, has no way of being expressed as a sum of symmetric and skew-symmetric bilinear forms.
A change of basis from a standard (in some sense) basis V to another basis V may result in a better structured matrix of a bilinear form B(u, v) which may be more suitable for computational or other purposes. This is especially so for the symmetric and the skew-symmetric bilinear forms:
Theorem. If B(u, v) is a symmetric bilinear form on a finite dimensional vector space V, over a field F of characteristic ¹ 2, there exists an ordered basis b of V such that [B]b is diagonal.
Proof: Since ([v]b )¢ [B]b [u]b = ([v]g )¢ [g ]b ¢ [B]b [g ]b [u]g , we have [B]g = [g ]b ¢ [B]b [g ]b , for any two ordered bases b and g of V. Hence it is sufficient to show that given any n´n symmetric matrix A over the field F, there exists an n´n non-singular matrix C such that C¢ AC is diagonal. For this we show that there exists a succession of elementary row and the same elementary column operations that turn A into a diagonal matrix. If a11 ¹ 0, we subtract ai1/a11 times the first row from the i-th followed by the subtraction of the same times the first column from the i-th, for 2 £ i £ n. (If a11 = 0 but some aj1 ¹ 0, we add j-th row and column to the first to arrive at the case where a11 ¹ 0). Now the matrix is of the form
![]() ,
,
where E is (n-1)´(n-1), from which the result follows by an induction on n. [If ch (F) = 2, aj1 + a1j = 2aj1 = 0, and the argument fails!]. #
Corollary 1. If V is a finite dimensional vector space over a field F of ch (F) ¹ 2 in which for every c Î F there exists a b Î F such that c = b2 and if B(u, v) is a symmetric bilinear form on V, there exists an ordered basis b of V such that [B]b is of the block diagonal canonical form
![]() .
.
where I is the r´ r identity matrix, where r is the rank of B and the 0's denote the possibly non-existent zero matrix blocks.
Proof: It follows from the diagonal form by dividing each row and column containing a non-zero diagonal entry c = b2 by b. [Note that in the complex field C any c can be written as a b and indeed any field F could be extended to one in which the equation: x = c has a solution for any c Î F.] #
Corollary 2. If V is a finite dimensional vector space over R and if B(u, v) is a symmetric bilinear form on V, there exists an ordered basis b of V such that [B]b is of a block diagonal canonical form diag (Is, -It, 0).
Proof: The result follows from the diagonal form after a division of each row and column containing a non-zero diagonal entry by the positive square root of the magnitude of the diagonal entry. #
Note that the Sylvester's inertia theorem implies that s denotes the number of positive eigen values and t the number of negative eigen values of any representing matrix [B]b of B and that t+s = r, the rank of B. In this case of the real field, the number s-t is called the signature of the symmetric bilinear form B(u, v). Note that the signature and the rank of B determine the canonical form diag (Is, -It, 0) completely, and are independent of the choice of a diagonalizing basis.
Theorem. If B(u, v) is a skew-symmetric bilinear form on a finite dimensional vector space V, over a field F of characteristic ¹ 2, there exists an ordered basis b of V such that [B]b is of a block diagonal canonical form diag (0, J, J, , J), in which 0 denotes a (possibly non-existent) zero matrix,
J = ![]() ,
,
and the rank of B equals twice the number of copies of the J-blocks.
Proof: It is sufficient to take a skew-symmetric matrix A over F and show that it is possible to reduce it to the required block diagonal form by a succession of elementary row and the same elementary column operations. To begin with note that since ch F ¹ 2, the diagonal elements of A are all zero and aij = -aji. Assume the result for k´k matrices for all k £ n-1, as an induction hypothesis. For 1´1 matrices the result is true. If ai1 = 0 for all i, the result for A follows from the induction hypothesis. If ai1 ¹ 0, for some i and i ¹ 2, interchange the i-th row with the second and the i-th column with the second column (if i = 2, we directly proceed to the next stage). Now a21 ¹ 0. Divide the second row by a21 and the second column by a21. In the resultant matrix, which continues to remain skew-symmetric, a21 = -a12 = 1. Now for each j such that 3 £ j £ n, subtract aj1 -times the second row from the j-th and subtract aj1 -times the second column from the j-th column to arrive at the form
![]() ,
,
where E is an (n-2)´(n-2) skew-symmetric matrix. By the induction hypothesis, it could be further reduced to the form diag (J, 0, J, ... , J), from which the required form is obtained by an interchange of rows and the corresponding columns that take the 0 diagonal block to the top left corner. The assertion concerning the number of J-blocks follows since each of it is of rank 2. #
PROBLEMS
1. Show that B is a symmetric (skew-symmetric) bilinear form on Fn iff for a symmetric (skew-symmetric) matrix A Î Fn´ n , B(x, y) = y¢ Ax, (x, y Î F). Also show that the set of such symmetric (skew-symmetric) bilinear forms forms a subspace of the space of bilinear forms on F and find its dimension.
2. If for a bilinear form B on a vector space V, and LB, RB : V ® V¢ are defined by (LBu)(v) = B(u, v) = (RBv)(u), show that LB = RB iff B is symmetric and that B is skew-symmetric iff LB = - RB .
3. If F is not of characteristic 2, show that every bilinear form can be written as a sum of a symmetric and a skew-symmetric bilinear form. What happens if ch F = 2?
4. Which of the following define bilinear forms on Rn? Which of them are symmetric and which are anti-symmetric? (a) B(x, y) = 0; (b) B(x, y) = (x1+x2+y1+y2)2 - (x12+x22+y12+y22); (c) B(x, y) = (x1+y1)2 - (x2-y2)2; (d) B(x, y) = x1y1 x2y2; (e) B(x, y) = x1y2 x2y1; (f) B(x, y) = x1y1 + x2y2 x1y2 x2y1.
5. Find all symmetric (skew-symmetric) bilinear forms on Fn, for 1 £ n £ 3, when F equals: (i) R, (ii) C, and, (iii) Z 2.
6. If V is an n-dimensional vector space over a field F, prove that dim B(V, F) = n2. Do the subsets consisting of symmetric and skew-symmetric bilinear forms on V constitute subspaces of B(V, F)? If so, what are their dimensions?
7. If B is a non-degenerate symmetric bilinear form on a finite dimensional vector space V, show that there exists an isomorphism h : L(V) ® L(V) such that h 2 = I and B(Tu, v) = f(u, h (T)v), u, v Î V. Is the h unique? Does such an h exist even if B is degenerate? Consider the same questions if B is skew-symmetric. Find an h when V = F2, B(x, y) = y¢ Ax, and A equals:
(i) ![]() , and, (ii)
, and, (ii) ![]() .
.
8. Find a basis for the space of all symmetric (skew-symmetric) bilinear forms on Rn.
9. Characterize the fields F for which the following is true: If F(x, y) is a symmetric and G(x, y) a skew-symmetric bilinear form on Fn and F + G = 0, then F = G = 0.
10. If V is an n-dimensional vector space over a field F of characteristic different from two, show that the equation (Pf)(u, v) = [f(u, v)-f(v, u)]/2, f Î B(V, F), defines a projection. Characterize the range and the null space of P and deduce that r(P) = n(n-1)/2 and and n(P) = n(n+1)/2.
11. Let C Î Fn´ n. Consider the linear operator T on the vector space B(Fn, F) given by (TCB)(x, y) = B(Cx, Cy). Prove that: (a) T is singular iff C is singular; (b) the subspaces of symmetric and skew-symmetric bilinear forms are invariant under T; and, (c) T is a projection if C is a projection.
12. Show that a non-zero skew-symmetric bilinear form B on R3 is precisely of the form B(x, y) = f (x)j (y) - j (x)f (y), where f and j are linearly independent linear functionals. Are f and j unique?
13. Show that a skew-symmetric bilinear form B of rank £ 2, on a finite-dimensional vector space V over a field F of characteristic different from 2, can be written as: B(u, v) = f (u)j (v) - j (u)f (v), where f and j are linear functionals.
14. If f and g are skew-symmetric bilinear forms on Cn , show that there exists a non-singular A Î Cn´ n such that f(Ax, Ay) = g(x, y) for all x, y iff f and g have the same rank. For what fields other than C does the result remain valid?
15. Find the matrix of the form: f((x1, y1), (x2, y2)) = x1y1-x2y2, on Z 2(2), in each of the following bases: {(1, 0), (0, 1)}, {(1, 1), (1, 0)}, {(1, 2), (4, 3)}.
Quadratic Forms
Taking the vector y to be the same as the vector x in a bilinear form B(x, y) Î B(Fn, F) we get a so called quadratic-form on F , which therefore is an expression of the form Q(x) = x¢ Ax, (x Î Fn, A Î Fn´ n), which is a second degree homogeneous expression in the components of x. Conversely, any second degree homogeneous expression Q(x) = S1£ i£ n S1£ j£ n aijxjxi, is a specialization of the bilinear form y¢ Ax, obtained by putting y = x. Note that given a quadratic form there exist many bilinear forms associated with it. It is because a quadratic form constrains only the cross sums aij+aji , and not the individual aij and aji , i ¹ j. If ch F ¹ 2, the quadratic form Q(x) is associated with a unique symmetric bilinear form, namely, B(x, y) = y¢ Bx, where bii = aii, 1 £ i £ n and bij = (aij+aji )/2, 1 £ i ¹ j £ n. If F is of characteristic two this is no longer true, e.g., the quadratic form x1x2 on Z22 arises from a bilinear form y¢ Ax precisely when A equals one of the following non-symmetric matrices:
![]() ,
, ![]() .
.
More generally, if V is a finite dimensional vector space over a field F, a quadratic form Q : V ® F, may be defined by Q(v) = B(v, v), v Î V, where B(u, v) is a bilinear form in V. The set of all quadratic forms on V may be denoted by Q(V, F). It is clear that under the usual addition and scalar multiplication of functions Q(V, F) is a vector space over F, which is a subspace of the vector space of all functions from V to F.
PROBLEMS
1. If F is of characteristic 2, show that A over F is symmetric iff A is skew-symmetric.
2. If F is not of characteristic 2, prove that every quadratic form Q(x) on F n can be represented by a symmetric matrix A, i.e., Q(x) = x¢ Ax, x Î F , where A¢ = A. What happens if ch F = 2?
3. If ch F = 2, show that any quadratic form over Fn can be written as Q(x) = x¢ Ax, where A is upper triangular.
4. Find all matrices A such that Q(x) = x¢ Ax = 0 for all x Î Fn .
5. Show that a quadratic form Q satisfies (a) the homogeneity: Q(cv) = c2Q(v), and, (b) the parallelogram law : Q(u+v) + Q(u-v) = 2[Q(u)+Q(b)].
6. If Q Î Q(V, F), prove that B(u, v) = [Q(u+v)-Q(u-v)]/4 Î B(V, F) satisfies Q(u) = B(u, u), provided ch F ¹ 2.
7. Let V be a finite dimensional vector space over a field F. Show that S(V, F) contains a subspace isomorphic to Q(V, F). Find the condition under which Q(V, F) is isomorphic to S(V, F) itself. Describe the related isomorphisms explicitly, and if possible, without reference to a basis.
8. If Q is a quadratic forms on V and T Î L(V), verify that QT(u) = Q(Tu), u Î V defines another quadratic form. Show that the map h : Q(V, F) ® Q(V, F), defined by h T(Q) º TQ = QT, where QT(u) = Q(Tu), u Î V, is a linear operator on Q(V, F) and that it is invertible iff T is invertible. Is the correspondence T ® h T one-one?
9. For the quadratic form Q(x)= ax2 + [c(b2/a)]x22, (a ¹ 0) on F2, consider the set U of all upper triangular matrices A Î F2´ 2 such that Q(Ax) = ax12 + 2bx1x2 + cx22. Show that: (a) if ch F = 2, the set U is a singleton, and, (b) if ch F ¹ 2, U has four elements.
10. Find all possible matrices A such that Q(Ax) = x12 x22, Q being the F2 quadratic form given by Q(x) = x1x2.
11. For the quadratic form q(x1, x2, x3) = x1x2 + x22 + x1x3, show that there exists an invertible linear operator U on R(3) such that (Uq)(x1, x2, x3) = x12 x22 + x32. [Uq(v) º qU(v) º q(Uv)].
12. If A Î Rn´ n is symmetric and q is the quadratic form on Rn given by q(x) =S1£ i, j£ n aijxixj, prove that there is an invertible linear operator U such that (Uq)(x) = S1£ i£ n cixi2 , where ci = ± 1, or 0, and moreover that ci2 = 1, 1 £ i £ n, iff A is non-singular.
13. If A Î Rn´ n is symmetric and q is the quadratic form on Rn given by q(x) =S1£ i, j£ n aijxixj, prove that q(x) = 0, for all x in Rn iff A = 0. Deduce that if f(x, y) is a symmetric bilinear form on Rn, with q(x) = f(x, x) the associated quadratic form, then Uq is of the form S1£ i£ n cixi2 iff f(Ux, Uy) = S1£ i£ n cixiyi. [Uq(v) º q(Uv)].
14. Let V be the real vector space of all n´n complex matrices. Show that q(A) = tr A¢ A, A Î V, defines a quadratic form on V. If f denotes the bilinear form determined by q, show that f is non-singular (and positive definite) on the subspace W of real matrices in V. Is f non-singular on V as well?
15. If V2 is the real vector space of all 2´ 2 hermitian matrices, show that q(A) = det A, A Î V2, defines a quadratic form q on V2. Determine the signature of the associated symmetric bilinear form f and prove that f is negative definite on the subspace W2 of V2 of matrices of trace 0.
16. If f(Ax) = f(x) º x12 x22, A Î C2´ 2, prove: A = ![]() , c Î C. Is the converse true?
, c Î C. Is the converse true?
Sesqi-Linear and Hermitian Forms
A sesqi-linear form S(x, y) on Cn is a map S : Cn´Cn ® C that is linear in the first component x: S(ax+bz, y) = aS(x, y) + bS(z, y), and conjugate linear in the second component y : S(x, ay+bz) = a* S(x, y) + b* S(x, z). [Here a* denotes the complex-conjugate of a]. It is clear that S(x, y) is a sesqui-linear form iff there exists an A Î C such that S(x, y) = y* Ax, x, y Î Cn.
More generally, a sesqui-linear form on a vector space V over K (R or C) is a map S : V´ V ® K which is linear with respect to the first argument and conjugate linear with respect to the second: S(cu+v, w) = cS(u, w) + S(v, w) S(u, cv+w) = c* S(u, v) + S(u, w) for all u, v, w Î V and all c Î K. Note that if K = R, a sesqui-linear form is nothing but a bilinear form.
A sesqui-linear form S on a vector space V over K is called hermitian if S(u, v) = [S(v, u)]* , u, v Î V. If S is a sesqui-linear hermitian form, the form H(v) = S(v, v), (v Î V) is called a hermitian form on V. Thus, on V = Cn, the form H(x) = x* Ax, where A is a hermitian matrix, is a hermitian form which takes only real values for whatever x Î Cn. The converse is also true, so that:
Theorem. The form H(x) = x* Ax takes real values for all x Î Cn iff A is hermitian.
Proof: If x* Ax is real for every x Î Cn, each eigenvalue of the hermitian matrix i(A* -A) is zero, so that the spectral theorem is applicable. #
PROBLEMS
1. If S(x, y) = y* Ax and T(x, y) = y* Bx are sesqui-linear forms such that S(x, y) = T(x, y) for all x, y Î Cn, prove that A = B.
2. Prove that the set S of all sesqui-linear forms on a vector space V over K is a vector space with the usual addition and scalar multiplication of functions. If dim V = n, what is dim S ?
3. If V is a finite dimensional inner product space and S is a sesqui-linear form on V, there exists a unique linear operator T on V such that S(u, v) = (Tu, v) for all u, v Î V, and the map t : S ® t (S) = T is a natural isomorphism of the vector space S of sesqui-forms onto L(V, V).
4. If V is a finite dimensional inner product space and t is the natural isomorphism from S to L(V, V) show that the equation (S, T) = tr (t (S)t (T)* ) defines an inner product on the space S of sesqui-linear forms on V, with the property that (S, T) = Sj, k S(uk, uj)[T(uk, uj)]* for every orthonormal basis {u1, , un} of V.
5. If S is a sesqui-linear form and b = {v1, , vn} is an ordered basis of V the matrix [S]b = A, with entries ajk = S(vk, vj), (1 £ j, k £ n) is called the matrix of S in the ordered basis b . Show that S(u, v) = [v]b * [S]b [u]b .
6. If t is the natural isomorphism of S onto L(V, V) and b is a basis of V, what is the relationship between [S]b and [t (S)]b ?
7. If S is a sesqui-linear form on a finite-dimensional complex inner product space V, show that there exists an orthonormal basis b of V in which the matrix of S is upper-triangular.
8. If V is finite dimensional and b is an ordered basis of V, show that S is Hermitian iff [S]b is hermitian.
9. If T is a linear operator on a finite dimensional inner product space space V over K, show that the sesqui-linear form S defined by S(u, v) = (Tu, v) is Hermitian if and only if T is self-adjoint.
10. A sesqui-linear form form S on a complex vector space is Hermitian iff S(v, v) is real for every v.
11. A linear operator T on a complex finite-dimensional inner product space V is self-adjoint iff (Tu, u) is real for each u Î V.12. Principal Axis Theorem. A sesqui-linear form S on a finite dimensional inner product space V is Hermitian iff there exists an orthonormal basis b of V such that [S]b is a real diagonal matrix.
13. If S(x) = x* Ax, and T(x) = y* Bx, are two hermitian forms and S(x) = T(x) for all x Î Cn, prove that A = B.
14. Show that a hermitian form S(x) = x* Ax is zero for all x Î Cn iff A = 0.
15. Show that the quadratic form Q(x) = x¢ Ax vanishes for all x Î C2, where A is the non-zero hermitian matrix given by:
A = ![]() .
.
16. Let x be an approximate eigenvector of a matrix A. If the corresponding eigenvalue l is estimated by minimizing the hermitian form P Ax-l xP 22 = x* [(A-l I)* (A-l I)]x, show that the estimate of the eigenvalue is given by the Rayleigh quotient l = x* Ax/x* x.
17. Which of the following functions f(x, y) defined for x, y Î C2 , are sesqui-linear forms on C2
(a) f(x, y) = (x1-2y1)2-(x2-2y2); (b) f(x, y) = (x1+y1)2x2y2; (c) f(x, y) = 1; (d) f(x, y) = (x1-2y2)-(x2-2y1)2; (e) f(x, y) = x1y2-x2y1; and, (f) f(x, y) = 0?
18. Is f(x, y) = y* Ax an inner product on C, where
A = ![]() ?
?
19. Let V be a complex vector space and f a sesqui-linear form on it which is also symmetric, i.e., f(u, v) = f(v, u), for u, v Î V. Is it true that f = 0?
20. If f(x, y) = 2x1y1+3x2y2+23x1y2+23x2y1, show that there exists an ordered basis b of R2 in which the form f is represented by the diagonal matrix diag (1, -1). Find such a basis b . Is it unique?
21. If f(x, y) = 2x1y1+3x2y2+x1y2+x2y1, show that there exists an ordered basis b of R2 in which the form f is represented by the diagonal matrix diag (1, 1). Find such a basis b . Is it unique?
22. If f(x, y) = 2x1y1+3x2y2 +Ö 6x1y2+Ö 6x2y1, show that there exists an ordered basis b of R2 in which the form f is represented by the diagonal matrix diag (1, 0). Find such a basis b . Is it unique?
23. A sesqui-linear form f on a real or complex vector space V is called positive if f is Hermitian and f(u, u) > 0 for all u ¹ 0. Verify that f is a positive form on V iff <u, v> = f(u, v)is an inner product on V.
24. A sesqui-linear form f on a real or complex vector space V is called non-negative if it is Hermitian and f(u, u) ³ 0 for every u Î V. A non-negative form f satisfies all but one of the properties of an inner product. Name this missing property and prove that f is a non-negative form iff f+g is a positive form for all positive forms g.
25. If f is a positive form on V = Kn, there is a p.d. matrix A such that f(x, y) = y* Ax = <x, y> is an inner product. If the columns uj of an n´n matrix U over K are orthonormal in this inner product, use x = S1£ j£ n uj(uj)* Ax, x Î Kn to deduce that A-1 = UU* .
26. For an invertible n´n A over a field F, prove the equivalence of the following statements: (a) there exists a non-singular lower-triangular matrix L, such that the matrix U = AL is upper triangular; (b) the following minors of A are non-zero
Ñ
k(A) = det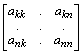 , 1 £ k £ n.
, 1 £ k £ n.
27. Let f be a sesqui-linear form on a finite-dimensional vector space V over K and let A be its matrix in some ordered basis b of V. Prove that f is a positive form if and only if there exists a non-singular and upper-triangular matrix U such that A = UU* .
Characterizations of a Positive Definite Matrix
Theorem. If If S(x) = x
* Ax is a hermitian form on Cn, the following statements are equivalent: (1) A is positive definite. (2) The eigenvalues of A are all positive. (3) D m = |Am| > 0, 1 £ m £ n, where Am is the principal m´m submatrix of A (Sylvester's criterion). (4) The coefficients of the characteristic polynomial fA(x) = |xI-A| = xn + a1xn-1 + + an-1x + an, are real and alternate in sign, i.e., sgn ai = (-1)i, 1 £ i £ n. (5) Each leading sub-matrix (a sub-matrix whose diagonal lies along the diagonal of the matrix) of A is positive definite.Proof: As S(x) = x
* Ax is a hermitian form, A is hermitian.(1)
Þ (2): Let (l , x) be an eigenpair. Then 0 < (Ax, x) = l (x, x) Þ l > 0.(2)
Þ (1): Let (l i, ui), 1 £ i £ n, be orthonormal eigenpairs of A. Let 0 ¹ x = S aiui Þ at least one ai ¹ 0. Then (Ax, x) = S l i|ai|2 > 0.(1)
Þ (3): (1) Þ (2) Þ |A| > 0. Considering (z | 0)¢ = x ¹ 0 that have the last n-m components zero, 0 < x* Ax = z* Amz Þ Am is positive definite and so is of a positive determinant. [Other proofs of the same follow from the Sturmian separation theorem and the LL* -decomposition].(3)
Þ (1): It is trivial for n = 1. Assume for n-1. By the Sturmian sepapration theorem n-1 of the eigen values of A are +ve. As |An| > 0, it follows that the remaining eigenvalue is also +ve. Hence (2) Þ (1). [Also follows from the LL* -decomposition].(5)
Þ (1): As A itself is a leading submatrix of A.(1)
Þ (5): Let a leading submatrix B be determined by the i(1), i(2), ... , i(k)-th rows and columns. Let y Î Ck be non-zero. Define x Î Cn by xi(j) = yj , j = 1 £ j £ k and xi = 0, otherwise. Then x ¹ 0, and therefore y* By = x* Ax > 0. Hence B is p.d.(1)
Þ (4): In fA(x) = |xI-A| = xn + a1xn-1 + + an-1x + an, the coefficient ak is (-1)k -times the sum of the determinants of all leading submatrices of A of order k, so that by (1) Þ (5), ak is of sign (-1)k.(4)
Þ (1): If the coefficients alternate in sign fA(x) cannot have a negative or a zero root. Hence A being hermitian, all of its eigen values are +ve Þ (2) Þ (1). This completes the proof. #An analogous result for positive semi-definite matrices is:
Theorem. If A is an n
´n hermitian matrix, the following statements are equivalent: (1) A is positive semi-definite. (2) The eigenvalues of A are all non-negative. (3) Each leading submatrix of A is of a determinant ³ 0. (4) The coefficients of the characteristic polynomial fA(x) = |xI-A| = xn + a1xn-1 + + an-1x + an, satisfy (-1)iai ³ 0, 1 £ i £ n. (5) Each leading submatrix of A is positive semi-definite.Proof: A is positive semi-definite
Û for every Î > 0, Ae = A + e I is positive definite. From this remark and the previous theorem, it follows that (1) Þ (2)-(5). Also each of (5) and (2) Þ (1). To prove (3) Þ (1), note that (3) Þ (4) Þ (1).Remark: The statement (3) cannot be replaced by
D m ³ 0, m = 1 £ m £ n. For instance, the matrix![]()
is not p.s.d.
PROBLEMS
1
. If A is an n´n p.d. matrix and B is an n´m matrix of rank m, show that B* AB is p.d.2. If A is p.d. show that A-1 exists and is p.d.
3. Let A be p.d. and B hermitian n
´ n matrices. Then there is a non-singular C such that C* AC = I, and, C* BC = diag [d1, d2 , , dn). Show that |B-l A| = 0 iff l = di for some 1 £ i £ n, and that |B-l A| = |C* C|P 1£ i£ n (di-l ).4. Let A11, A22 be p.d. matrices. If
A = ![]() , B =
, B = ![]() ,
,
show that
BAB
* =and that A is p.d. iff A11 A12A22-1A12
* is p.d. Deduce that A is p.d. iff A = TT* , where T is upper triangular and non-singular.5. If A is p.d. and G = A-1, show that aiigii
³ 1, for all i.6. Show that there exists a lower triangular non-singular n
´n L such that A = LL* iff f(x, y) = y* Ax is an inner product on Cn.7. A linear operator T on a finite-dimensional inner product space V over K (C, or, R) is called non-negative if T is self-adjoint and (Tv, v) ³ 0, for all v Î V. T is called a positive linear operator if T is self-adjoint and (Tv, v) > 0, for all v ¹ 0. If A is an nxn matrix over K, show that the following statements are equivalent: (i) A : x ® Ax is a positive operator on Kn with the standard inner product (x, y) = y* x; (ii) S1£ j£ n S1£ k£ n akj xjxk* > 0 whenever x1, , xn Î K are not all zero (i.e., A is a positive definite matrix); (iii) <x, y> = y* Ax is another inner product on K ; (iv) A = LL* for some invertible nxn lower triangular matrix L over K; (v) A is self adjoint and all the eigenvalues of A are positive; and, (vi) A = P2 for some positive definite P over K.
8. Let V be a finite dimensional inner product space. Is it true that given any two non-zero vectors u, v Î V, there exists a positive definite operator T Î L(V) such that v = Tu?
9. For what matrix operators Rq on R2 given by
Rq = ![]() , (anticlock-wise rotation by an angle q),
, (anticlock-wise rotation by an angle q),
does there hold (Rq x, x) > 0, 0 ¹ x Î R2 iff -p /2 < q < q /2? Which of such Rq are self adjoint and therefore positive?
10. Compute the adjoint of a matrix operator A with respect to an inner product of the form <x, y> = (Px, y) on Cn, where P is an appropriate n´n matrix and the last inner product is the standard one . Charaterize A that are self adjoint with respect to <× , × >.
11. The representer of a linear functional f in an inner product space V is defined to be an element f Î V, if such an element exists, such that f(v) = (v, f ), v Î V. Show that a representer is unique.
12. Show that any linear functional on a finite dimensional inner product space has a representer. Find the representer of the linear functional f(x) = a1x1 + a2x2 + + anxn, ai Î K, in the inner product space Kn, with the inner product <x, y> = y*Px.
13. If H and A are positive linear operators on a finite-dimensional inner product space V, prove that aA+hH is positive for all a, h > 0, but that AH and HA need not be positive. What can you say about AHA?
14. Is the matrix
A = ![]()
positive definite? Is <x, y> = y* Ax an inner product in C3? If so find an orthonormal basis of C3 with respect to this inner-product.
15. Find a positive definite matrix P such that ![]() = P2.
= P2.
16. Which of the 2´2 matrices
![]()
are positive semi-definite? Which are positive definite?
17. Show that the diagonal entries of a positive definite matrix are all positive and that the largest entry, or entries, of such a matrix must also occur along the diagonal.
18. Give an example of an n
´ n hermitian matrix which has all its leading minors non-zero, but which is not a positive matrix.19. Give an example of an n
´ n matrix which has all its leading minors positive, but which is not a positive matrix.20. Give an example of an n
´ n symmetric matrix which has all its principal minors positive, but which is not a positive matrix.21. Let
V be a finite-dimensional inner product space. If T and U are linear operators on V, we write T £ U if U-T is a positive semidefinite operator. Prove the following: (a) T £ U and U £ T iff T = U. (b) If T £ U and U £ S, then T £ S. (c) If T £ U and 0 £ S, it need not be that ST < SU.22. Let
V be a finite-dimensional inner product space. Prove that an orthogonal projection E of V onto a subspace W is is a positive semi-definite operator and that it is positive definite iff W = V. Deduce that if W ¹ V and c is a secalar, the operator cI+E is positive definite iff c > 0, in which case there exist precisely four self-adjoint linear operators T such that T = cI+E.23. If p is a positive number, prove the positive definiteness of
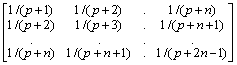 .
.
24. If T is self-adjoint, show that that there is a unique real number c such that the operator cI+T is positive semidefinite and singular.
25. If S and T are positive semi-definite, show that ST is positive semi-definite iff ST = TS.
26. If S and T are positive semi-definite show that the eigenvalues of ST are non-negative.