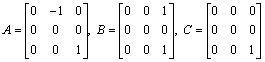 .
.Chapter 6
SIMULTANEOUS TRIANGULIZATION AND DIAGONALIZATION
An alternate treatment of triangulization and diagonalization is based on the notion of a T-conductor of an element x
Î V into a T-invariant subspace W . Using T-conductors, results on simultaneous triangulization and diagonalization of classes of matrices could be obtained more easily.
Characteristic and Minimal Polynomials
As we already know, the characteristic polynomial fA(x) º |xI-A|, of an n´ n square matrix A is a monic polynomial in x of degree n and the characteristic polynomial of a linear operator T : V ® V is given by fT(x) = |xI-[T]|, where [T] is the matrix of T with respect to some basis b of V . Note that if g is any other basis [T]g = [g ]b -1[T]b [g ]b is similar to [T]b , so that |xI-[T]g | = |xI-[T]b |, i.e., fT(x) is independent of the choice of a basis.
Since c is an eigenvalue of T iff there is a non-zero v such that Tv = cv, i.e., (cI-T)v = 0 has a non-trivial solution. Hence c is an eigenvalue of T iff fT(c) = 0, i.e., c is a root of the characteristic polynomial of T. The largest m such that (x-c) is a factor of fT(x) is called the algebraic multiplicity of the eigenvalue c. By the geometric multiplicity of an eigenvalue c, we mean the largest number of linearly independent solutions of Tx = cx, which is the dimension of the eigenspace V T,c = {x Î V : Tx = cx} of T associated with the eigenvalue c.
Let (Cij(x)) denote the matrix of co-factors of xI-A, Aj the j-th column of A and ek the k-th unit vector in F n. Then, as d ik|xI-A| = S 1£ j£ n Ckj(x)(xd ij-aij), fA(A)ek = S 1£ i£ n d ik fA(A)ei = S 1£ i£ n [S 1£ j£ n Ckj(A) (d ijA-aijI)]ei = S 1£ j£ n Ckj(A) [S 1£ i£ n (d ijA-aijI)]ei = S 1£ j£ n Ckj(A) [S 1£ i£ n (d ijAi-aijei)] = S 1£ j£ n Ckj(A) [Aj- Aj] = 0. As k is arbitrary, we have the Cayley-Hamilton Theorem that every square matrix A (or linear operator T) satisfies its own characteristic equation, i.e., fA(A) = 0 (or, fT(T) = 0).
A polynomial p(x) such that p(T) = 0 is called an annihilating polynomial for T, The monic polynomial pT(x) of least degree such that pT(T) = 0, is called the minimal polynomial of T. Its unicity as well as the fact that pT | fT follows from the remainder theorem. If c is an eigen value of T and v is an associated eigenvector, 0 = pT(T)v = pT(c)v, and as pT | fT it follows that c is a zero of pT iff c is a zero of fT.
Example. Let us compute the minimal polynomial p(x) of each of the matrix operators
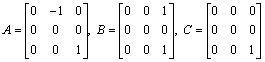 .
.
The characteristic polynomial f(x) for each of these is simply x2(x-1). Since the minimal polynomial divides the characteristic polynomial and a root of the characteristic polynomial is necessarily the root of the minimal polynomial, the possibilities for the minimal polynomials of these matrices are only x(x-1) and x2(x-1). Denoting these by p1(x) and p2(x), respectively, we have:
p1(A) = A(A-I) = 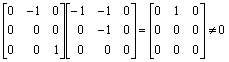 ,
,
p1(B) = B(B-I) = 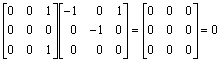 ,
,
p1(C) = C(C-I) = 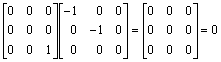 ,
,
Hence the minimal polynomials of A, B and C are x2(x-1), x(x-1), and x(x-1), respectively.
Any polynomial q(x) such that q(T) = 0 is said to annihilate (or kill) T. Given a v Î V , a monic polynomial p(x) of least degree such that p(T)v = 0, is called T-annihilator of v. Using the remainder theorem it follows that a T-annihilator of v exists and is unique.
PROBLEMS
1. Find the characteristic and minimal polynomials of the following matrix operators on R 2:
![]() .
.
2. Find the characteristic and minimal polynomials of the of the identity and the zero operators on F n.
3. Find the eigenvalues, eigenvectors and the characteristic and the minimal polynomials of the following matrix operator A on F 3 by inspection. Hence deduce its diagonalizability by constructing a basis of F 3 consisting of its eigenvectors.
A = 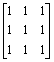 .
.
4. Find its characteristic and minimal polynomials and determine if the matrix
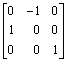
is similar over the field R to a diagonal matrix? Is it similar over the field C to a diagonal matrix?
5. Show that the intgral operator (Tf)(x) = ò [0,x] f(t) dt, f Î C[0,1], the space of continuous real valued functions on [0,1], has no characteristic values, whereas the differential operator (Df)(x) = f'(x), f Î C1[0,1], the subspace of continuously differentiable functions on [0,1], has an infinity of them.
6. If T is a diagonalizable operator on V with fT(x) = (x-a)p(x-b)q … (x-c)r, (p, q, … , r ³ 1), show that operators that commute with T constitue a subspace of L(V ) of dimension p2 + q2 + … + r2 iff a, b, ... , c are distinct.
7. Let B Î F n´ n. Define TA = BA and SA = AB, A Î F n´ n. Prove that the matrix B and the operators T and S possess the same eigenvalues. Do they have the same characteristic and minimal polynomials too?
8. Let fA = pA, fB = pB and (fA, fB) = 1. If E = ![]() , prove that fE = pE . Deduce that the matrix
, prove that fE = pE . Deduce that the matrix
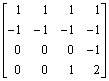
has fE(x) = pE(x) = x2(x-1)2. Could E be similar to a diagonal matrix?
9. Let V be a ten dimensional vector space and let T be a linear operator on V . If T100 = 0, prove that T10 = 0.
10. Find 3x3 matrices for which the minimal polynomials are: (a) x, (b) x2, and (c) x3. What are the corresponding characteristic polynomials?
11. What is the minimal polynomial of (a) the identity operator on the vector space V = {0}, and (b) the differential operator D = d/dx, defined by Dxk = kxk-1, over the vector space of polynomials of degree £ n? Does the minimal polynomial of D exist on the vector space of all polynomials? What is the minimal polynomial of the identity operator over the same space?
12. If f (x) = (x-a)p(x-b)q … (x-c)r where a, b, … , c > 0 and p + q + … + r = n, show that trace (A/n) ³ (det A)1/n.
13. Let A, B Î F n´ n. Do the matrices AB and BA have the same: (a) characteristic values, (b) characteristic polynomials, and (c) minimal polynomials?
14. Let P be the operator on R 2 which reflects each vector about the x-axis, i.e., P(x,y)¢ = (x,-y)¢ . Is P linear? Show that the minimal and the characteristic polynomials of P are the same?
15. Verfy that the degree of the minimal polynomial of T on V (¹ {0}) is the smallest m such that the operators I, A, A2, … , Am are l.d., and then that if c0I + c1T + … + cmTm = 0, pT(x) = c0 + c1x + … + cmxm.
16. The row vector of an m´ n matrix A is the 1´ mn matrix written in the partitioned form as vecR A = [R1 | R2 | … | Rn], where Rj denotes the j-th row of A. Similarly the column vector of A (written vec A º vecC A) is the mn´ 1 matrix obtained by stacking the successive columns of A, the second below the first and so on. Verify that the maps A ® vecR A, and, A ® vecC A, are vector space isomorphisms of F m´ n onto F 1´ mn and F mn´ 1, respectively. Deduce that a set S = {A : A Î S} is l.i. iff {vecR A : A Î S} is so, and similarly for the column case.
17. If the characteristic polynomial of an operator is of form f(x) = P 1£ i£ m (x-l i)k(i), (k(i) ³ 1, 1 £ i £ m), the possibilities for the minimal polynomial p(x) are only from amongst the k(1)´ k(2)´ … ´ k(m) polynomials p(x) = P 1£ i£ m (x-l i)j(i), (k(i) ³ j(i) ³ 1, 1 £ i £ m). Construct examples to show that each of these possibilities indeed holds.
18. Let I denote the n´ n identity matrix, x Î F and x Î F n . Determine the characteristic and minimal polynomials of the following block-partitioned matrix A and verify that they are equal. What happens in the case of the matrices B and C?
![]() .
.
T-Invariant Subspaces and T-Conductors
If T is a linear operator on a vector space V , a subspace W of V is called T-invariant if TW = {Tw : w Î W } Ì W . Let W be T-invariant. Then, the restriction T|W (of T to W ) is an operator on W in its own right. Let v Î V º V n. The monic polynomial s(x) = sTv,W (x) of least degree such that s(T)v Î W , is called the T-conductor of v into W (when acting on v, sTv,W (T) takes it to W ).
Since pT(T)v = 0 Î W , using the remainder theorem it follows that sTv,W (x) exists and is unique. Moreover, if q(T)v Î W , using the T-invariance of W and the remainder theorem, q(T)v = sTv,W (T)Q(T)v + R(T)v, where the remainder R has degree < deg sTv,W (x), we have R(T)v Î W . Hence R = 0, else we have a monic polynomial (namely, R divided by its coefficient of highest degree) of a degree smaller than sTv,W (x) that conducts v into W , contradicting the definition of a T-conductor. Note that if v Î W , sTv,W (x) = 1, and that if v Î V \W , then deg sTv,W ³ 1.
PROBLEMS
1. A linear operator T on a vector space V is said to possess no proper invariant subspaces if the only subspaces invariant under T are {0} and V . Show that A given below possesses no proper invariant subspaces in R 2. What are the invariant subspaces of A in C 2?
A = ![]() .
.
2. If W is T-invariant prove that the minimal polynomial for the restriction operator T|W divides the minimal polynomial for T.
3. If U Ì W are T-invariant subspaces of V , prove that sTv,W (x) divides sTv,U (x) for all v Î V .
4. Prove the existence of a v Î V such that sTv,{0} = pT . What is sTv,V ? What is sT0,W for any T-invariant W ?
5. Prove that the restriction of an operator T to its eigenspace corresponding to an eigenvalue c is simply c times
the identity operator.
6. Which of the following matrices
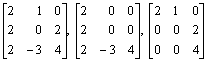
are similar over the field of real numbers to upper triangular matrices? For them find such upper triangular matrices.
7. Prove that any matrix A over a field F , satisfying A2 = A, is similar to a diagonal matrix.
8. Prove that any matrix A over C , satisfying Am = A for some integer m ³ 2, is similar to a diagonal matrix. Is the result true for every field F ? Is the result true for every algebraically closed field?
9. Prove that the restriction T|W of a diagonalizable operator T to a T-invariant subspace W is diagonalizable.
10. Let U and W be T-invariant such that sTv,U = sTv,W , for all v Î V . Prove that U = W .
11. Consider the operator T : F n´ n ® F n´ n, defined by TA = A+A¢ . Let W denote the set of all symmetric n´ n matrices. Is W T-invariant. If so find sTB,W when: (a) B is symmetric, (b) B is skew-symmetric, and (c) B is neither symmetric nor skew-symmetric.
12. Compute the A-conductor of (1,2,3)¢ to W = {x Î R 3 : x3 = 0} for the following A's:
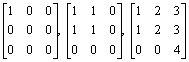 .
.
Triangulization and Diagonalization
Let < … > denote the span of whatever is inside the angular bracket symbols < and >. Thus, <v1, v2, … , vk> = span {v1, v2, … , vk}, <S> = span S, and <v1, v2, … , vk, S1, S2, … , Sl > = span [{v1}È {v2}È … È {vk}È S1È S2È ... È Sl].
Lemma. Let W be a proper (here ¹ V ) T-invariant subspace of V n. If pT or fT is a product of linear factors (i.e., has the form P i (x-ci)r(i), r(i) ’s being positive integers), there exists a u Î V n\W such that sTu,W (x) = x-c, where c is one of the ci 's (or equivalently Tu Î <u,W >).
Proof: For any v Î V n\W , sTv,W is at least of degree one and divides pT and fT. Writing sTv,W (x) = (x-c)q(x), where x-c is any of its linear factors and putting u = q(T)v Î V n\W , the first assertion of the lemma follows. The second equivalent assertion is clear from it. #
Let T be a linear operator on a vector space V = V n(F ). T is called triangulable if there is an ordered basis b of V such that [T]b is upper triangular.
Theorem (Triangulization). T is triangulable iff pT (or, equivalently, fT) is a product of linear factors in F .
Proof: W 0 = {0} is a proper T-invariant subspace of V . Hence there is a v1 Î V \W 0 such that Tv1 Î <v1,W 0> = <v1> = W 1, say. As W 1 is also proper T-invariant, there is v2 Î V \W 1 such that Tv2 Î <v2,W 1> = <v1, v2> = W 2, say. Continuing in this fashion we have vk Î V such that W k = <v1, v2, … , vk>, 1 £ k £ n, such that W n = V and Tvk Î W k, 1 £ k £ n, so that b = {v1, v2, … , vn} triangulizes T.
Conversely, if T is triangulized by b and c1, c2, … , cn Î F are the diagonal elements of [T]b , as already seen, fT(x) = P 1£ i£ n (x-ci) so that fT is a product of linear factors in F . Since pT | fT also pT is a product of linear factors in F . #
Corollary. fT is a product of linear factors iff pT is so.
Proof: If pT is a product of linear factors, T is triangulable and then fT is a product of linear factors. The converse is already clear. #
As far as the triangulization of T is concerned we have seen that the polynomials fT and pT play a similar role. However, the diagonalization of T is characterized by pT and not fT :
Theorem (Diagonalization). T is diagonalizable iff pT is a product of distinct linear factors, i.e. pT(x) = P i (x-ci), where ci 's are distinct.
Proof: If T is diagonalizable and ci 's are distinct eigenvalues of T, P i (x-ci) annihilates T and consequently pT which divides it is a product of distinct linear factors. Conversely, if pT is a product of distinct linear factors, let W denote the subspace spanned by the eigenvectors of T. (It is called the eigen-space of T). If W is not the whole of V , the T-conductor s(x) of some v Î V \W , is of the form x-c for some eigenvalue c of T. Since x-c divides pT, let pT(x) = (x-c)q(x). Then 0 = (T-cI)q(T)v, so that q(T)v Î W . But then x-c | q(x) so that (x-c)2 | pT(x), a contradiction. It follows that W = V , so that any set of linearly independent eigenvectors of T form a basis of V which diagonalizes T. #
It may be stressed that T is diagonalizable iff any maximal set of linearly independent eigenvectors of T is a basis of V . Moreover, T on an inner product space is unitarily diagonalizable iff T is diagonalizable and eigenvectors of T corresponding to distinct eigenvalues are orthogonal.
Example 1. Consider the matrix A Î F 3´ 3 with aij = 1 for all 1 £ i, j £ 3 Since A2 = 3A, the polynomial x(x-3) annihilates A. Since A is not a scalar matrix, pA(x) = x(x-3). Hence A is diagonalizable iff ch F ¹ 3.
Example 2. If
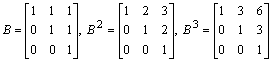 .
.
Since, obviously, no monic polynomial of degree 2 annihilates B and B3 = aB2 + bB + cI = 0, leads to equations: 6 = 3a + b, 3 = 2a + b = 0 and 1 = a + b + c = 0, having the unique solution a = 3, b = -3 and c = 1, it follows that pB(x) = x3 -3x2 +3x-1 = (x-1)3. (Alternately, since pB(x) has to divide the characteristic polynomial fB(x) = (x-1)3 and has degree larger than 2, pB must then equal pA). Since pB(x) is not a product of distinct linear factors, B cannot be diagonalizable.
Example 3. Since the field C of complex numbers is algebraically closed any n´ n complex matrix is triangulable. Of the 2´ 2 matrices
A = ![]() , B =
, B =![]() , C =
, C = ![]() , E =
, E = ![]() ,
,
A is diagonalizable over C , but not over R ; B is diagonalizable over R ; and none of C and E is diagonalizable over C . Note: pA(x) = x2+1, pB(x) = x2-1, and, pC(x) = pE(x) = x2.
PROBLEMS
1. If an n´ n matrix A has n distinct eigenvalues then A is diagonalizable.
2. If a 2´ 2 real or complex matrix A does not have distinct eigenvlaues then A is digonalizable iff A is already a diagonal matrix. True, or false?
3. Some positive power of a non-diagonalizable operator T is diagonalizable iff T is nilpotent. True, or false?
4. Let A be a real n´ n matrix. Then A is triangulable over R iff fA(x) has n real roots. Moreover, A is diagonalizable over R iff A is diagonalizable over C and triangulable over R . If A is diagonalizable over R , it is diagonalizable over C .
5. If A is diagonalizable, show that the operator T defined by TB = AB-BA is diagonalizable.
6. For what a, b and c are the following matix operators diagonalizable on F 4?
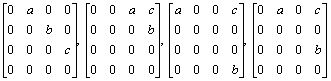 .
.
7. Prove that any 0 ¹ A Î R 2´ 2 such that A2 = 0, is of type ![]() and is similar over R to
and is similar over R to ![]() .
.
8. Prove that any 2x2 complex matrix is similar over C to a matrix of one of the types ![]() .
.
9. Let A and B be n´ n matrices over a field F and 0 ¹ c Î F . Prove that if (I - cAB) is invertible, then I - cBA is
invertible and (I - cBA)-1 = I + B(c-1I - AB)-1A. Hence, deduce that AB and BA have precisely the same characteristic values in F . What if A and B are respectively m´ n and n´ m?
10. Show that any 2x2 real symmetric matrix is similar over R to a diagonal matrix. Can you generalize the result for any n´ n real symmetric matrix?
11. Show that the following matrix is not diagonalizable over R , but that it is triangulable over R ? Also compute a basis that triangulizes it:
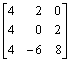 .
.
12. Prove that any projection (A2 = A) matrix A is diagonalizable.
13. If a linear operator T is diagonalizable (triangulabel) and W is T-invariant, prove that the restriction operator T|W is diagonalizable (triangulable). Construct an operator T which is neither triangulable nor diagonalizable, but has a T-invariant subspace W such that T|W is diagonalizable (triangulable).
14. Let T be a linear operator on a finite-dimensional vector space over an algebraically closed field F . Prove that T is diagonalizable if and only if T is annihilated by some polynomial over F having distinct roots.
15. If every subspace of a vector space V is invariant under a linear operator T, show that T must be a scalar multiple of the identity operator.
16. Let T be the indefinite integral operator (Tf)(x) = ò [0,x] f(t) dt, on the space C[0,1] of continuous real functions on the interval [0,1]. Which of the subspaces consisting of: (a) polynomial functions, (b) continuously differentiable functions, (c) functions which vanish at x = 0, and (c) functions which vanish at x = 1/2, invariant under T?
17. True or false? If a complex triangular matrix A is: (a) similar, and, (b) unitarily similar to a diagonal matrix, then A must already be diagonal.
18. Let T be a linear operator on a finite-dimensional vector space over an algebraically closed field F . Let q be a polynomial over F . Prove that c is an eigenvalue of q(T) iff c = q(t), where t is an eigenvalue of T. What happens if F is not algebraically closed?
19. Let AÎ F n´ n and T and U be the linear operators on F n´ n defined by T(B) = AB, and, U(B) = AB-BA. True or false? (a) If A is diagonalizable, then T is diagonalizable, (b) If A is diagonalizable, then U is diagonalizable.
20. Prove that a 3´ 3 real matrix is either triangulable over R , or is diagonalizable over C .
21. Prove that there exist no more than n+1, n´ n dissimilar matrices A satisfying A2 = A.
22. Prove that the maximum number of dissimilar n´ n matrices A satisfying Am = I, is n+m-1Cm-1.
Simultaneous Triangulization and Diagonalization
Lemma. Let C be a commuting family of triangulable linear operators on V = V n. Then, if W (¹ V ) is a C -invariant subspace of V , there exists a u Î V \W such that Tu Î <u,W >, T Î C .
Proof: Let F be a maximal linearly independent subfamily of C . Then F has a finite number of elements T1, T2, ... , Tm, say, and it is sufficient to prove the lemma with C replaced by F . Let W 0 = V n. Consider the subspace W 1 of v Î W 0, such that T1v Î <v,W >. Note that W Ì W 1. Then v Î W 1 implies that T1Tkv = TkT1v Î <Tkv, W >, 1 £ k £ m. Hence W 1 is F -invariant. By a previous lemma W Ì W 1 ¹ W .
Let W 2 denote the subspace of v Î W 1, such that T2v Î <v,W >. Again v Î W 2 implies that T2Tkv = TkT2v Î <Tkv,W >, so that W 2 is F -invariant W Ì W 2 ¹ W , and moreover, as W 2 is a subspace of W 1, if v Î W 2 then Tjv Î <v,W >, j £ 2. Continuing in this fashion, inductively, in m-steps we construct the subspaces W 1, W 2, W 3 , … , W m such that W Ì W m Ì W m-1 Ì … Ì W 2 Ì W 1, W m ¹ W , W m is F -invariant, and for any v Î W m, Tv Î <v,W >, T Î C . It is now clear that any u Î W m\W is a required vector. #
Theorem (Simultaneous Triagulization). A commuting family C of triangulable linear operators T on V n is simultaneously triangulable.
Proof: The subspace W = {0} is proper C -invariant. Using the previous lemma there is an v1 Î V n\W 0, such that Tv1 Î <v1>, T Î C . Hence <v1> is proper C -invariant. Again there is a v2 Î V n\<v1>, such that Tv2 Î <v2,v1>, T Î C . Continuing in this fashion we have v1, v2, v3, … , vn such that vk+1 Î V n\<v1,v2, … ,vk>, and Tvk+1 Î < v1, v2, … ,vk,vk+1>, k = 0, 1, ... , n-1. It is then clear that b = {v1, v2, … , vn} is a basis of V n that simultaneously triangulizes all T e C . #
Theorem (Simultaneous Unitary Triagulization). A commuting family C of triangulable n´ n matrices over R , or C , is simultaneously unitarily triangulable.
Proof: Using the previous theorem, it is similar to that of the Schur's lemma. Thus the Gram-Schmidt process applied to a basis that simultaneously triangulizes C gives us a required basis. #
Corollary (Simultaneous Unitary Diagonalization). A commuting family C of unitarily diagonalizable (i.e., normal) operators is simultaneously unitarily diagonalizable.
Proof: Since a unitarily diagonalizable (and therefore a normal) operator is trivially unitarily triangulable, using the previous theorem we can simultaneously unitarily triangulize C . Since, for a normal operator a unitarily triangulized form is diagonal, the result follows. #
PROBLEMS
1. If C is a family of simultaneously unitarily diagonalizable matrices (operators), show that C is necessarily a commuting normal family. Show by examples that the commutativity, however, is not necessary for simultaneous (unitary) triangulability.
2. If T, S Î C , a family of simultaneously triangulable operators show that TS-ST is nilpotent. (Is the converse true?!)
3. If A, B, C, D are n´ n commuting complex matrices, and E is the 2n´ 2n block partitioned matrix
![]() ,
,
show that there exists an ordering of the eigenvalues ai, bi, ci, di, 1 £ i £ n of A, B, C, D, respectively, such that the 2n -eigenvalues of E are given by {ai + di ± Ö [(ai – di)2 + 4bici ]}/2, 1 £ i £ n.
Simultaneous Diagonalization
Theorem. Let
C be a commuting family of linear operators on a finite dimensional vector space V , the minimal polynomial of each of which is a product of distinct linear factors. Then, there exists an ordered basis b of V that simultaneously diagonalizes C , and conversely.Proof: If dim
V = 1, the result is trivial. Hence to proceed by induction, assume it for spaces of dimension < n. Let dim V = n. Without loss of generality we may assume that C has at least one operator T that is not scalar (i.e., a scalar multiple of the identity) operator. Let c1, c2, … , ck deote the set of distinct eigenvalues of T. Then k ³ 2. Let W i denote the eigenspace of T corresponding to its eigenvalue ci. Then 1 £ dim W i £ n-1 and W 1 Å W 2 Å … Å W k = V . Let S Î C and ui Î W i. Then T(Sui) = STui = ciSui, so that Sui Î W i. Thus each W i is invariant under C (i.e., invariant under every operator in C ). Hence the restrictions of members of C to W i, being commutative and diagonalizable as operators on W i, are simultaneously diagonalizable on W i by an ordered basis b i, say. It follows that the pooled ordered basis b = {b 1, b 2, … , b k} of V simultaneously diagonalizes C . The converse is trivial, since any two diagonal matrices commute. #
PROBLEMS
1
. If A and B commute and are diagonalizable, show that AB is diagonalizable, but not conversely.2. If A is diagonalizable, show that the operator T defined by TB = AB+BA is diagonalizable.
3. If A m´ m and B commute and are diagonalizable, show that the operators S, T on F n´ n defined by SX = BX+XA, TX = AX+XB are simultaneously diagonalizable.
4. Let T be a linear operator on a finite-dimansional space such that the minimal polynomial pT(x) of T is a product of distinct linear factors. Prove that any linear operator which commutes with T is a polynomial in T iff pT(x) = fT(x).
5. Verify that the follwing sets of matrices are simultaneously diagonalizable and find the respective diagonalizing bases:
(a) ![]() ; (b)
; (b) ![]() .
.
6. Let C commonly denote a family of (a) simultaneously diagonalizable (b) simultaneously triangulable and (c) a commuting family of 3´ 3 complex matrices. Find an upper bound on the number of linearly independent matrices in C ? Are your bounds sharp? Generalize for the n´ n case.
7. Let A Î F n´ n and TA be the linear operator on F n´ n, defined by TA(B) = AB-BA. Consider the family F of linear operators T obtained by letting A vary over the family C of: (a) commuting matrices, (b) simultaneously diagonalazible (c) simultaneously triangulable matrices, and (d) all matrices in F n´ n. In which of the cases is the family F : (a) commuting, (b) simultaneously diagonalizable, and (c) simultaneously triangulable?