 .
.Chapter 7
THE PRIMARY AND THE CYCLIC DECOMPOSITION THEOREMS
1. The Primary Decomposition Theorem
If the minimal polynomial pT(x) of a linear operator T on a finite dimensional vector spave
V has a maximum of k distint prime polynomial factors, the primary decomposition theorem enables us to decompose V into a direct sum of k T-invariant subspaces on each of which the minimal polynomial of the restriction of the operator T has a simple form, thereby reducing the dimensionality of the problem in studying T through the restrictions of T to these subspaces. The primary decomposition theorem, combined with the cyclic decomposition theorem in the sequel, also leads to a derivation of the important Jordan canonical form of an operator.Lemma. Let T be a linear operator on a vector space
V . Let P1, P2, … , Pk be monic polynomials, such that (Pi, Pj) = 1, i ¹ j, and let P(T) = 0, where P = P1P2 … Pk . Let V i = N (Pi(T)). Then:(i)
V i 's are T-invariant;(ii)
V = Å 1£ i£ k V i = V 1 Å V 2 Å … Å V k;(iii) If Ti = T|
V i and gi = P 1£ j£ k, j¹ i Pj, gi(Ti) is non singular.Proof: The polynomials gi , 1
£ i £ k, are relatively prime, i.e., (g1, g2, … ,gk) = 1. [For, if a prime g | gi for all i, g | Pj for some j. But then g Œ gj, else g has to divide Pi for some i ¹ j and then Pi and Pj would not be relatively prime, a contradiction]. Hence there exist polynomials h1, … , hk such that 1 = S 1£ i£ k gihi. Then I = S 1£ i£ k gi(T)hi(T) = S 1£ i£ k Ei, say, where Ei = gi(T)hi(T). It follows that Ei2 = Ei (i.e. Ei 's are projections), and, EiEj = 0, i ¹ j. Putting W i = R (Ei), we have V = Å 1£ i£ k W i = W 1 Å W 2 Å … Å W k. Since Ei 's commute with T, W i 's are T-invariant. Note that Pi(T)Ei = 0 (as Pi(T)Ei = Pi(T)gi(T)hi(T)). Hence W i Ì V i. Also, if v Î V i , then v = E1v + … + Eiv + … + Ekv = Eiv Î W i (if j ¹ i, Ej has a factor Pi(T)). It follows that V i Ì W i. Hence W i = V i. Finally, gi(T)hi(T) = Ei is an identity on W i, and so gi(Ti) is non-singular as gi(Ti) = gi(T|V i ). This completes the proof. #Corollary 1. (Primary Decomposition Theorem). Let T be a linear operator on a vector space
V over a field F . If pT = P 1£ i£ k piri, where the pi 's are distinct irreducible monic polynomials, and if W i = N (piri(T)), 1 £ i £ k, then:(i) each
W i is T-invariant;(ii)
V = W 1 Å … Å W k;(iii) if Ti = T|
W i, pTi = piri.Proof: Only the last assertion is to be verified. Let qi = pTi. Putting q =
P 1£ i£ k qi, q(T) = q1(T)q2(T) … qk(T) = 0, since for wi Î W i, q(T)wi = q(T)wi = q(Ti)wi = (P j¹ i qj(Tj))qi(Ti)wi = 0. Hence, pT | q = P 1£ i£ k qi. As W i = N (piri(T)), qi | piri. so that, q | pT, and being being monic, q = pT. #Problem. Find the primary decomposition of
F 4 relative to each of the following matrix operators: .
.
Corollary 2. If E1, … , Ek are the projections associated with the primary decomposition theorem, then each Ei is a polynomial is T;hence if an operator S commutes with T it commutes with each Ei, i.e., each W i is invariant under S.
Proof: Recall that Ei = gi(T)hi(T). #
Problem. Is the the converse true, i.e., does S commute with T if S commutes with each Ei?
Corollary 3. Let fT = P1P2 … Pk, where Pi 's are pair-wise relatively prime and monic. Then fTi = Pi. [Pi 's, Ti 's as in the Lemma.]
Proof: By the Lemma, pooling the bases of Vi 's with fi º fTi , P1P2 … Pk = fT = f1 … fk. [Later we will see that every prime factor of the characteristic polynomial is also a factor of the minimal polynomial;and that if q is a factor of p then q(T) is singular]. Since P2(T1) … Pk(T1) is non-singular, by the Lemma, no prime factor of f1 is a factor of P2 … Pk. It follows that f1 | P1 (by exhausting the prime factors). Similarly, fi | Pi , 1 £ i £ k. As P fi = P Pi, fi = Pi, 1 £ i £ k . #
Corollary 4. Let T be triangulable (i.e., pT or fT is a product of linear factors). Then there exist unique nilpotent N and diagonalizable D operators such that ND = DN and T = D + N. Moreover D and N are polynomials in T.
Proof: Let pT(x) = P 1£ i£ k (x-ci)mi. Let Ei 's be the projections associated with the primary decomposition V = W 1 Å W 2 Å … Å W k , where W i = N (( ciI-T)di). Then Ei 's are polynomials in T and EiEj = d ijEi. Hence, D = S 1£ i£ k ciEi is diagonalizable and is a polynomial in T. Hence, N = T – D is a polynomial in T and therefore ND = DN. Since I = Å 1£ i£ k Ei, N = S 1£ i£ k (ciI-T)Ei. Hence if m = max mi , we have Nm = S 1£ i£ k (ciI-T)mEi = 0, so that N is nilpotent, and T = D + N. If also T = D1 + N1, D1N1 = N1D1, D1 is diagonalizable and N1 is nilpotent, then D1 and N1 commute with T (e.g., D1T = D1(D1+N1) = (D1+N1)D1 = TD1) and so with D and N. Hence D-D1 = N1-N is diagonalizable (both D and D1 being so and commuting and so being simultaneously diagonalizable) and also is nilpotent as (N–N1)d = 0,if d = max {2d1, 2d2 : Nd1 = N1d1 = 0}. It follows that D-D1 = 0 implying that D = D1 and N = N1. #
Jordan Canonical Form (Assuming the primary decomposition). Let T be nilpotent. As W = T(V ) is T-invariant, let S denote the restriction of T to W . As dim(W ) < dim(V ), by induction on the dimension of space, we can assume that S has a Jordan basis È 1£ i£ m{wij Î W : 1 £ j £ mi} in W with Twi1 = 0, 1 £ i £ m and Twij = wij-1 , 1 < j £ m , 1 £ i £ m. Since T(S i³ 1 S j³ 1 cijwij ) = S i³ 1 S j>1 cijwij-1, it is clear that B 1 = {wi1: 1 £ i £ m} is a basis of N (S). We can extend B 1, by choosing B 2 = {uk Î V \W :1 £ k £ l}, so that span{B 1 È B 2} = N (T). Finally, as W = T(V ), there exist vi Î V such that Tvi = wimi , 1 £ i £ m. It is clear that vi 's are linearly independent. Noting that T(S i³ 1 S j£ mi aijTjvi + S bkuk) = S i³ 1 S j<mi aij Tj+1vi, it follows that B = {Tjvi : 0 £ j £ mi, 1 £ i £ m} È B 2 is a Jordan basis for T in V , proving the result for a nilpotent T.
For a general T on V , if fT(x) = P 1£ i£ p (x-ci)ni, where ci 's are distinct, gi(x) = fT(x)/(x-ci)ni are relatively prime so that for some polynomials hi(x) there holds 1 = S i gi(x)hi(x). It follows that V = W 1 Å W 2 Å … Å W p, a direct sum, where W i = gi (T)h (T)V = N ((T-ciI)ni), 1 £ i £ p, are T-invariant. As the operator Ti = T-ciI is nilpotent on W i, Ti has a Jordan basis B i in W i. From this it is clear that B = B 1 È B 2 È … È B p is a Jordan basis for T in V . #
PROBLEMS
1
. Let T be the linear operator on R 3, represented in the standard ordered basis by the matrix .
.
Show that pT can be expressed in the form p = p1p2, where p1 and p2 are monic and irreducible over the field of real numbers. With W i = N (pi(T)) and Ti = T|W i, choose some ordered bases B i for the subspaces W i and determine the matrix of Ti in the basis B i, and hence that of T with respect to the pooled basis B = {B 1, B 2}.
2. Find the commuting diagonalizable and nilpotent parts for whichever of the following matrix operators over R 3 it is possible:
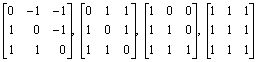 .
.
3. What are the commuting diagonalizable and nilpotent parts, resp., of diagonalizable and nilpotent operators?
4. What are the commuting diagonalizable and nilpotent parts of the differentiation operator on P n, the space of all polynomials of degree less than or equal to n over a field F .
5. If T is a linear operator on a vector space V such that pT(x) = (x-c1) r1 … (x-ck)rk , (ci 's distinct). Show that W = N ((T-ciI) ri) consists precisely of all those vectors v Î V for each of which there exists a positive integer m such that (T-ciI)mv = 0, and that dim W i = di, where fT(x) = (x-c1) d1 … (x-ck) dk.
6. Let T be a triangulable linear operator on a finite dimensional vector space V over a field F and let D be the diagonalizable part of T. Prove that if g is a polynomial over F, g(T) is triangulabel and the diagonalizable part of g(T) is g(D).
7. Show that every linear operator T of rank one is triangulable and that one of its diagonalizable and nilpotent parts is zero.
8. Characterize all linear operators T, on a finite-dimensional vector space V over a field F , that commute with every diagonalizable linear operator on V . Is any of them not a scalar multiple of the identity operator?
9. Let A Î F n´ n, and define TA(B) = AB-BA, B Î F n´ n. Prove that A is triangulable, diagonalizable, or, nilpotent iff T is so.
10. In which of the 2´ 2, 3´ 3, 4´ 4 and 5´ 5 cases do there exist non-similar nilpotent matrices having the same minimal polynomial.
11. If V = W 1 Å … Å W k is the primary decomposition for T and W a T-invariant subspace, show that W = (W Ç W 1) Å … Å (W Ç W k).
12. If D is an n´ n diagonal matrix and N an n´ n upper triangular matrix, is it true that the diagonalizable and the nilpotent parts of the matrix A = D + N are D and N, respectively? Would you make a concession if the diagonal entries in D were distinct?
13. If T is a linear operator on V with pT = pm, where p is irreducible over the scalar field F , prove that the T-annihilator sTu of 0 ¹ u Î V is of the form pk, 1 £ k £ m;and moreover, that any such pk is the T-annihilator of some 0 ¹ u Î V .
14. What are all diagonalizable operators T such that pT = fT.
15. Show that all nilpotent linear operator on an n-dimensional vector space V have identical characteristic polynomials. Do they have the same minimal polynomials too?
16. Let T = D + U, where D is a diagonal matrix and U is a strictly upper triangular matrix. Prove that D is a polynomial in T iff D commutes with U.
2. T-Cyclic Subspaces and Vectors
A subspace
W of a vector space V is called a T-cyclic subspace if there is a w Î V such that W = Z (w;T) = <w,Tw,T2w, … > (<S> denoting the span of the set S) and we say that W has a T-cyclic vector w. If v is a T-cyclic vector for V , we simply say that v is a T-cyclic vector. Clearly, Z (u;T) = {P(T)u: P a polynomial}.Let sTv(x) denote the T-annihilator of v, i.e., the monic polynomial of least degree such that sTv(T)v = 0. Let sTv be of degree k so that sTv(x) = a0 + a1x + … + ak-1xk-1 + xk. Then
B = {v, Tv, … , Tk-1v} is a basis of Z (v;T) and the matrix of T|Z (v;T) with respect to the basis B isC = 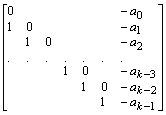 .
.
The matrix C is called the companion matrix of the monic polynomial P(x) = a0 + a1x + … + ak-1xk-1 + xk. Obviously, pT|
Z (v;T) = fT|Z (v;T) = sTv = pC = fC = sTv. Also note that given any monic polynomial P(x) = a0 + a1x + … + ak-1xk-1 + xk, C is the matrix, w.r.t the standard basis {e1, … ,ek} of F k, of the linear operator S defined by Sei = eI+1, i = 1, … , k-1, Sek = -(a0e1 + a1e2 + … + ak-1ek). It follows that the characteristic and minimal polynomials of a companion matrix C (of any monic polynomial P) are identical.Lemma 1. If Q is a polynomial Q(T)
Z (v;T) = Z (Q(T)v;T).Proof: Q(T)
Z (v;T) = Q(T){P(T)v : P Î F [x]} = {Q(T)P(T)v : P Î F [x]} = {P(T)Q(T)v : P Î F [x]} = Z (Q(T)v;T). #Lemma 2. STP(T)v = sTv / (P, sTv ).
Proof: There exist polynomials Q and S such that (P, sTv) = PQ + sTvS. Let R(Pv) = 0.
Þ R(P,sTv)v = 0. Þ sTv | R(P, sTv). Þ sTv ¤ (P, sTv) ½ R. Finally, (sTv ¤ (P, sTv)(Pv) = (P/(P, sTv))sTvv = 0. #
PROBLEMS
1
. What linear operators on F 1 possess a cyclic vector? Show that a linear operator on F 2 possesses a cyclic vector iff it is not a scalar multiple of the identity operator. Is the result true in F n for n > 2.2. Does the matrix operator
A = 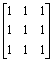
on
F 3 possess a cyclic vector? Show that the cyclic subspace generated by the vector (a,b,c)¢ is two dimensional iff a+b+c ¹ 0 and a = b = c does not hold.3. Prove that a diagonalizable operator on an n-dimensional vector space has a cyclic vector iff it has n-distinct eigenvalues.
4. Let A denote the matrix operator on
C 3 given byA = 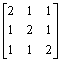 .
.
Show that
W = span {(1,1,1)¢ } is A-invariant. Find the A-conductor of x = (1,2,1)¢ into W . Is it different from the A-annihilator of x?5. If P is a polynomial and P(T) has a cyclic vector, then T has a cyclic vector. Is the converse true? What, if deg P = 1?
6. Prove: a nilpotent operator N on an n-dimensional vector space
V over a field F has a cyclic vector iff N ¹ 0.7. Prove that N is a nilpotent operator on an n-dimensional vector space
V and N ¹ 0, iff there is a basis b of V such that[N]
b =where I is the (n-1)
´ (n-1) identity matrix.8. Use computations, and not the theory, to show that the characteristic polynomial of the companion matrix of a monic polynomial is the polynomial itself.
9. Let
V have a basis {v1, … , vn} consisting of eigenvectors of a linear operator T possessing a cyclic vector. If v Î V , prove that Z (v;T) = V iff v = c1v1 + … + cnvn, where ci ¹ 0, 1 £ i £ n.10. Let U and T be linear operators on a finite-dimensional vector space
V . If T has a cyclic vector v and Uv = P(T)v, where P is a polynomial, prove that U = P(T) iff U commutes with T.
3. The Cyclic Decomposition Theorem
A subspace
W is called T-admissible if W is T-invariant and if for every polynomial g and every v Î V , g(T)v Î W implies that there exists a vector w Î W such that g(T)v = g(T)w.Lemma 1. Let
W 0 be T-invariant and let u Î V be such that sTu,W 0(x) is of maximal degree. Let W = W 0 + Z (u;T). Then, W is T-invariant, and, for any v Î V if sTv,W (T)v = w0 + P(T)u, (w0 Î W 0, P Î F [x]) then sTv,W (x) ½ P(x).Proof: Let P(x) = sTv,
W (x)Q(x) + R(x), where deg R < deg sTv,W (x). Let w = v - Q(T)u. Then sTw,W (x) = sTv,W (x), (as u Î W ) and sTw,W (T)w = w0 + R(T)u.Since sTw,
W ½ sTw,W 0, we can write sTw,W 0(x) = sTw,W (x)S(x), where S is a monic polynomial. Then S(T)R(T)u Î W 0. It follows that sTu,W 0 ½ SR. Therefore, if R ¹ 0, then deg (SR) ³ deg (sTu,W 0) ³ deg sTw,W 0 = deg (SsTw,W ) = deg (SsTv,W ), implying that deg R ³ deg sTv,W , a contradiction. Hence R = 0, and consequently, sTv,W ½ P. #Lemma 2. If
W 0 is T-admissible and sTu,W is of maximal degree, then W = W 0 + Z (u;T) is T-admissible.Proof: By Lemma 1, sTv,
W (T)v = w0 + sTv,W (T)Q(T)u, for some w0 Î W 0 and polynomial Q. Þ w0 = sTv,W (T)(v-Q(T)u) = sTv,W (T)w01, for some w01 Î W 0 (by T-admissibility of W 0). Þ sTv,W (T)v = sTv,W (T)(w01 + Q(T)u) = sTv,W (T)w, say, where w = w01 + Q(T)u Î W . Now, if P1(T)v Î W Þ P1(x) = sTv,W (x)Q1(x) Þ P1(T)v = Q1(T)( sTv,W (T)v) = Q1(T)( sTv,W (T)w) = P1(T)w, w Î W, proving that W is T-admissible. #Lemma 3. If
W 0 is T-admissible and W = W 0 + Z (u;T), there exists a v Î V such that W = W 0 Å Z (v;T) and sTv,W 0 = sTv = sTu,W 0.Proof: Let sTu,
W 0(T)u = sTu,W 0(T)w0, w0 Î W 0. Put v = u – w0. Then, sTu,W 0 = sTv,W 0 = sTv, and W 0 + Z (u;T) = W 0 + Z(v;T). Since W 0 Ç Z (v;T) = {0}, Þ W = W 0 Å Z (v;T). #Theorem (Cyclic Decomposition). Let
W 0 be a proper T-admissible subspace of a finite dimensional vector space V . Then there exist non-zero vectors u1, u2, … , ur Î V , with the respective T-annihilators p1, p2, … , pr such that pi+1 | pi , i = 1, 2, … , r-1 and V = W 0 Å Z (u1;T) Å … Å Z (ur;T). Moreover, the number r and the polynomials p1, p2, … , pr are invariants of the decomposition (i.e., they depend only on V , W 0 and T and not on ui 's).Proof: Applying Lemmas 2 and 3 successively, there exist u1, u2, … such that
W 1 = W 0 Å Z (u1;T), W 2 = W 1 Å Z (u2;T), … , W k = W k-1 Å Z (uk;T), … , are T-admissible and for some r, eventually culminate in V = W r = W r-1 Å Z (ur;T). Let pj = sTuj,W j-1 = sTuj. Since 0 = pi+1(T)ui+1 = (0 + p1(T)u1 + … + pi-1(T)ui-1 ) + pi(T)ui, Lemma 1, applied to ui+1 , W i-1 and W i , gives pi+1(x) | pi(x), i = 1, 2, ... r-1.To prove the invariance, finally, let also
V = W 0 Å Z (v1;T) Å … Å Z (vs;T) where vi ‘s are non-zero and qi = sTvi and put X k = X k-1 Å Z (vk;T), 1 £ k £ s. As dim W 0 < dim V it follows that s ³ 1. Then p1(T)V = p1(t)W 0 = p1(T)W 0 Å Z (p1(T)v1;T) Å … Å Z (p1(T)vs;T). It follows that p1(T)v1 = 0 and hence that q1 | p1. By symmetry, p1 | q1, so that p1 = q1. Since dim Z (u;T) = deg (sTu ) it follows that s ³ 2 (as dim X 1 = dim W 1 < dim V ).Next, p2(T)
V = p2(T)W 0 Å Z (p2(T)u1;T) = p2(T)W 0 Å Z (p2(T)v1;T) Å Z (p2(T)v2, T) Å … . Hence, p2(T)v2 = 0 so that q2 | p2. By symmetry p2 | q2 and hence p2 = q2. It follows that s ³ 3 (as dim X 2 = dim W 2 < dim V ). Continuing in this fashion, we get qi = pi for all possible i and that s = r. This completes the proof. #By the cyclic decomposition of
V relative to T, in the sequel, we shall mean the above cyclic decomposition of V relative to T when W 0 = {0}.Problem. Taking
V = F n and W 0 = span {(1, 0, 0, … , 0)¢ } find a cyclic decomposition of V relative to each of (i) T = I, (ii) T = 0, and (iii) T = diag (1, 2, ... , n).Corollary 1. Let
W 0 be T-invariant. Then W 0 has a complementary T-invariant subspace (i.e., a W such that TW Ì W and W 0 Å W = V ) iff W 0 is T-admissible.Proof: If
W 0 is T-admissible, by the cyclic decomposition theorem, W = Å 1£ i£ r Z (ui;T) is a required complementary T-invariant subspace. Conversely, let W be T-invariant and V = W 0 Å W . Let v = w0 + w Î V and let P(T)v = P(T)w0 + P(T)w Î W 0, (w0 Î W 0, w Î W ). Then by T-invariance and linear independence of W 0 and W , P(T)w = 0 and so P(T)v = P(T)w0, i.e., W 0 is T-admissible. #Corollary 2.(Generalized Cayley-Hamilton Theorem). If p = p1m
1 p2m2 … pkmr and V = W 1 Å … Å W r correspond to the primary decomposition of T, then fT = p1d1 p2d2 … prdr, where mi £ di = (dim W i)/(deg pi), 1 £ i £ r.Proof: With
W 0 = {0} in the cyclic decomposition theorem, sTu1 = pT. As sTui+1 | sTui, i = 1, … , r-1, Þ fT = P 1£ i£ r sTui = P 1£ i£ r pidi for some di ³ mi , i = 1, … , r. Since pimi = pTi , where Ti = T|W i , applying the result obtained so far to W i and Ti Þ fTi = pimi , where mi = (dim W i)/(deg pi ). But fT = P 1£ i£ r fTi = P 1£ i£ r pimi = P 1£ i£ r pidi Þ (as pi 's are irreducible (prime) polynomials) that di = mi. #Aliter: pTi = pimi and in the cyclic decomposition of
W i with W 0 = {0}, we have sTiu1 = pTi . As sTiuj+1 | sTiuj for all j. It follows that fTi = P j sTiuj = pidi where di´ (deg pi) = dim W i, from which we have fT = P 1£ i£ r pidi , where di = (dim W i)/(deg pi). #Corollary 3. PT = fT iff
V has a T-cyclic vector u.Proof: Apply cyclic decomposition theorem with
W 0 = {0}. If fT = pT (= p1) Þ r = 1 and V = {0} Å Z(u1;T) = Z(u;T), say. Conversely, if V = Z (u;T) = {0} Å Z (u;T), by the same theorem pT = sTu Þ deg pT = deg sTu = dim Z (u;T) = dim V Þ pT = fT . #Corollary 4. Every T-invariant subspace has a complementary T-invariant subspace iff pT is a product of distinct irreducible factors.
Proof: Suppose every T-invariant subspace has a complementary T-invariant subspace. Assume, on the contrary, that pT = p2q, where p is irreducible. Choose u
Î V such that v = p(T)q(T)u ¹ 0. Then there is a T-invariant subspace W such that: W = Z (v;T) Å W . We can write u = Q(T)v + w, where Q is a polynomial and w Î W . Then, v = p(T)q(T)u = p(T)q(T)w = 0, a contradiction.Conversely, let pT be a product of distinct irreducible factors, pT = p1p2 … pr , say. Consider the corresponding primary decomposition :
V = W 1 Å W 2 Å … Å W r, W i = N (pi(T)). Let W be a T-invariant subspace of V and write s(x) = sTu,W (x). Then, s(T)u =s(T)w1 + s(T)w2 + … + s(T)wr Î W . Letting Ei 's denote the projections associated with the primary decomposition, W ' Eis(T)u = Eis(T)wi = s(T)Eiwi = s(T)wi.Suppose wi
Ï W . If pi | s, then, of course, s(T)wi = 0; but if pi Œ s, using the existence of the polynomials Pi and S such that piPi + sS = 1, we have W ' S(T)s(T)wi = wi - Pi(T)pi(T)w1 = wi, a contradiction. Hence, if wi Ï W , then pi | s and therefore s(T)wi = 0. Putting w as the sum of wi 's belonging to W , s(T)u = s(T)w, showing that W is T-admissible. Hence, by the cyclic decomposition theorem, W possesses a complementary T-invariant subspace. This completes the proof. #The linear operators T for which pT is a product of distinct irreducible factors, are diagonalizable with respect to any super field of the field
F under consideration in which pT factors completely into a product of linear factors. Such operators are called semi-simple, that is next to simple (i.e., diagonalizable). It follows that if F is algebraically closed, the semi-simple operators are precisely the ones that are diagonalizable. It is also clear that a matrix A over a field F is semi-simple iff A is diagonalizable over G , where G is a super field of F in which fT splits (i.e., is a product of linear factors).
PROBLEMS
1
. Let T be a linear operator on a finite dimensional vector space V . If fT = pT, show that a linear operator U on V commutes with T iff it is a polynomial in T.2. Let T be the linear operator on
F 2 which is represented in the standard ordered basis by the matrix![]() .
.
Let u = (0,1)¢ and v = (1,0)¢ . Show that F 2 = Z (u;T) ¹ Z (v;T) and that there is no non-zero vector w Î F 2 with Z (w;T) disjoint from Z (v;T). Does T possess a proper T-invariant subspace? Does it possess a proper T-admissible subspace?
3. Let T be any linear operator on the finite-dimensional vector space V . Prove that the following statements are equivalent: (a) N (T) is T-admissible; (b) R (T) is T-admissible; (c) V = N (T) Å R(T); (d) if W is T-invariant and V = N (T) Å W , then W = R (T); and, (e) if U is T-invariant and V = R (T) Å U , then U = N (T).
4. Let T be a linear operator on a finite dimensional vector space V over a field F . Prove that if c Î F , S = T-cI and W is a T-invariant subspace of V , then W is T-admissible iff W is S-admissible.
5. If W 1, … , W k are T-invariant subspaces, V = W 1 Å … Å W k, and P is a polynomial, verify that P(T)V = P(T)W 1 Å … Å P(T)W k.
6. If u, v Î V have the same T-annihilators verify that for any polynomial P, also P(T)u and P(T)v have the same T-annihilator. Now, let us look for a polynomial Q such that for whatever u and v in V , whenever Q(T)u and Q(T)v have the same T-annihilator also u and v have the same T-annihilator. Show that such a non-constant polynomial Q exists. Characterise all such Q's.
7. Let T be the linear operator on F 4 which is represented in the standard ordered basis by the matrix
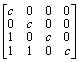 .
.
Find all the possible T-conductors of elements of F 4 into N (T-cI).
8. When is a nilpotent operator N semi-simple?
9. If N is nilpotent and f a polynomial is it true that the semi-simple part of f(N) is the scalar operator f(0)I?
10. If T is semi-simple, show that f(T) is semi-simple for any polynomial f.
11. Show that T is semi-simple iff for any polynomial f, f(T) = 0 iff f(T) is nilpotent.
12. Let F Ì G be fields and P an irreducible polynomial over F . Prove that P is a product of linear factors over G iff P is a product of distinct linear factors over G . Deduce that two semisimple linear operators T and S over a finite dimensional vector space V over F are similar iff fT = fS.
13. Let T be a linear operator on R 2, represented in the standard ordered basis by one of the matrices
![]() .
.
Verify that the T-invariant subspaces N (I-T) and R (I-T) do not possess complementary T-invariant subspaces. Generalize.
4. The Rational Form
A block diagonal matrix diag (C1,C2, … ,Cr) where Ci is a companion matrix of a monic polynomial pi and where pi+1 | pi , i = 1, … , r-1, is called a matrix in the rational form.
Problem. If C is a matrix in the rational form show that pC = p1 .
Theorem. Let T be a linear operator on a finite dimensional vector space
V . Then there exists a basis b of V such that [T]b is in the rational form. Moreover, the rational form of T is unique (i.e., if also [T]g is in the rational form, then [T]b = [T]g ).Proof: Using cyclic decomposition theorem with
W 0 = 0, we have V = Z (u1;T) Å Z ( u2;T) Å … Å Z(ur;T)where sTui | sTui+1, i = 1, ... , r-1. If deg sTui = di , and pi = sTui, then [T]b = diag (C1,C2, … ,Cr)where b = {b 1,b 2, … ,b r} where b i = {ui, Tui, … ,Tdi-1ui} and ci is the companion matrix of pi. For unicity, if qi+1 | qi, i = 1, ... , s-1, [T]g = diag (E1,E2, ... ,Es), (Ei companion matrix of qi) and g = {g 1, g 2, … ,g s} is a compatible de-pooling with g i = {vi1, vi2, … , vidi}, Þ that with vi = vi1, i = 1, ... , s, V = Z (v1;T) Å Z (v2;T) S … Å Z (vs;T) with sTvi | sTvi+1, i = 1, ... , s-1. Hence, by cyclic decomposition theorem, s = r, sTvi = sTui, and therefore [T]g = [T]b . #
PROBLEMS
1
. Find the minimal polynomials and the rational forms of each of the following matrix operators: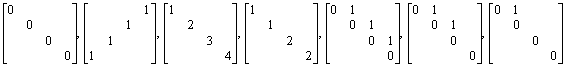 .
.
2. Find the minimal polynomials and the rational forms of each of the following real matrices:
![]() .
.
3. Let Q denote the rational field and T denote the linear operator on Q 3, represented in the standard ordered basis by
![]() .
.
Show that W = {(c,0,c)¢ : c Î Q } is T-admissible and determine the associated cyclic decomposition and the invariant factors.
4 For each of the following real matrices A find an invertible 3x3 real matrix P such that P-1AP is in rational form:
![]() .
.
5. If F is a subfield of C , find the possible rational form/s of the linear operator T on F 4 which is represented in the standard ordered basis by the matrix
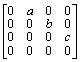 ,
,
keeping in mind the various possibilities for a, b, and c.
6. Show that, if n £ 3, any two n´ n matrices over a field F are similar iff they have the same characteristic polynomial
and the same minimal polynomial. Is the result true for n > 3?
7. Let F Ì G be two fields and let A be a matrix over F . Verify that the rational form of A, viewed as a matrix over G, is exactly the same as the rational form of A over F . Deduce that the minimal and the characteristic polynomials pA and fA of A are independent of whether A is regrded as a matrix over F or over the field G .
8. If F Ì G are two fields, prove that there does exist a matrix over G which is not a matrix over F but is such that its rational form is a matrix over F .
9. If F is a subfield of an algebraically closed field G and all the eigenvalues of an n´ n matrix A over G lie in F , prove that A over G is similar to a matrix B over F . Verify that the result is not necessarily true if the coefficients of the minimal polynomial of A, and not its eigenvalues, lie in F .
10. For any linear operator T on a finite-dimensional vector space V , show that there exists a vector u (called a separating vector for the algebra of polynomials in T) such that for any polynomial P, P(T)u = 0 implies that P(T) = 0.
11. Let T be a linear operator on a finite dimensional vector space V . Prove that u is a separating vector for the algebra
of polynomials in T iff sTu = pT.
12. If A and B are n´ n real matrices such that pA = pB = x2 +1, prove that A and B are similar.
13. If c Î F does not possess a square root in the field F , and A is an n´ n matrix over F such that A2 = cI, prove that n is even and that A is similar to the block partitioned matrix
![]() ,
,
I being the m´ m identity matrix with m = n/2.
14. If T is a linear operator on a finite-dimensional vector space V , no non-trivial T-invariant subspace in V possesses a complementary T-invariant subspace iff fT equals pT and, moreover, is a power of a polynomial irreducible over F .
15. If T is a diagonalizable linear operator, show that every T-invariant subspace is T-admissible, but that the converse is not necessarily true?
16. Prove that a linear operator T on a finite dimensional vector space V has a cyclic vector iff each linear operator that commutes with T is a polynomial in T.
17. If T is a linear operator on a finite-dimensional vector space V over a field F , prove that every non-zero vector in V is a cyclic vector for T iff fT is irreducible over F .
18. Let A Î R n´ n. If A as an operator on R n possesses no proper invariant subspaces, show that pA(x) = x2 + 2bx + c2, with |b| < c and b, c Î R . Deduce that A is diagonalizable with respect to C .
5. The Invariant Factors
The polynomials p1(x), p2(x), … , pr(x), associated with the rational form of T are called the invariants factors of T. If [T]
b is in rational form with pi 's denoting the invariant factors it is clear that the Smith normal form of l I-[T] is given by diag [1,1, … ,1,pr(l ),pr-1(l ), … ,p1(l )]. Since the Smith normal forms of l I-[T]b and l I-[T]g for any two bases b and g of V coincide, the invariant factors, as well as the rational form of T could be determined by finding the invariant factors of the l -matrix l I-[T] , where b is any ordered basis of V .Corollary. Two matrices are similar iff they have the same rational form.
PROBLEMS
1
. Prove that every matrix is similar to its transpose.2. If F Ì G are fields and A and B are matrices over F that are similar over G , prove that they are also similar over F .
3. Prove that every n´ n l -matrix is l -row equivalent to an upper triangular l -matrix.
4. Prove that A Î F n´ n has a cyclic vector if and only if all minors of xI-A of order n are relatively prime.
5. Let T be a linear operator on an n-dimensional vector space V over a field F and let q1(l ), … , qn(l ) denote the diagonal entries of the Smith normal form of l I-T. Prove that q1(l ) ¹ 1 iff T is scalar.
6. Find the rational form of a diagonal matrix with distinct eigenvalues ci 's of multiplicities mi, 1 £ i £ r?
7. Find the invariant factors and the rational form of the following matrix and determine if the matrix is diagonalizable over R :
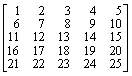 .
.
6. The Jordan Canonical Form
An r
´ r Jordan block is an r´ r matrix of type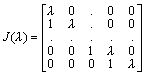 ,
,
in which all diagonal entries are the same scalar l , all sub diagonal entries are 1 and the remaining entries are 0. A 1´ 1 jordan block is simply the matrix [l ]. We call J(l ) an r-th order Jordan block corresponding to the eigen-value l . The transpose of J(l ) in which instead of the sub-diagonal entries being 1, the super diagonal entries are 1, is also called a Jordan block. However, presently, we will adhere to the first definition as given above.
Problem. What is the rational form of the above Jordan block?
A block diagonal matrix, diag [J1(l 1),J2(l 2), … ,Jr(l r)] in which Ji(l i) 's are Jordan blocks of certain sizes ni´ ni, is said to be a matrix in Jordan canonical form.
Theorem. If T is triangulable (i.e., pT = p(x-ci), a product of linear factors) there exists a basis b of V such that [T]b is in Jordan canonical form. Moreover, the Jordan canonical form is unique up to a permutation of the Jordan blocks.
Proof: Consider the primary decomposition V = W 1 Å W 2 Å … Å W r, of V with respect to T, with Ti = T|W i , pTi = (x-ci)di . Let Si = T –ciIi , Ii being the identity matrix of appropriate size. Then pSi = xdi and with W 0 = {0}, the invariant factors of Si on W i are of the form xk . Then the rational form of Si w.r.t. an appropriate basis b i is [Si]b i = diag [J1i(0), J2i(0), … ,Jkii(0)], where the blocks Jji(0) are Jordan blocks corresponding to l = 0. Here dim Jji(0) > dim Jj+1i(0). Hence [Ti]b i = [Si+ciIi] = diag [J1i(ci), J2i(ci), … ,Jkii(ci)]. Hence, with b = {b 1,b 2, … ,b r}, the pooled basis of V , [T]b = diag [J11(c1), J21(c1), … ,Jk11(c1), ... , J1r(cr), J2r(cr), … ,Jkrr(cr)], a Jordan canonical form. Let g be another basis s.t. [T]g is in Jordan canonical form. Since the diagonal entries of Jordan blocks are precisely the eigenvalues of T which are c1, c2, … , cr, without loss of generality we can assume the Jordan blocks permuted so that dim Jji ³ dim Jj+1i and [T]g = diag [J11(c1), J21(c1), … ,Jm11(c1), ... , J1r(cr), J2r(cr), … ,Jmrr(cr)], Let g = {g 1, g 2, … , g r} be a compatible partitioning where g I ’s constitute basis members corresponding to Jordan blocks corresponding to eigen value ci.
It is clear that W i = N((T-ciI)di) = span {b i}, as [(T-ciI)di]g = diag [X1,X2, … ,Xi-1,0,XI+1, … ,Xr], Xj 's are non-singular matrices and 0 is the zero matrix associated to the location of J-blocks corresponding to eigenvalue ci. Hence, with Ti = T|W i, [Ti –ci I]g i = diag [J1i(0),J2i(0), ... ,Jmii(0)], which is in rational form.
Similar consideration w.r.t. basis b leads to [Ti-ciI]b i = diag [J1i(0),J2i(0), ... ,Jkii(0)], a rational form. By the uniqueness of the rational form. It therefore follows that ki = mi, dim Jji(0) ’s in both [Ti-ciI]b i = diag [J1i(0),J2i(0), ... ,Jkii(0)] and [Ti –ci I]g i = diag [J1i(0),J2i(0), ... ,Jmii(0)] are the same for all i and j's. It follows therefore that [T]g = [T]b , after at most a permutation of Jordan blocks. #
PROBLEMS
1
. Are the matrices:![]()
similar?
2. Prove that two 3
´ 3 matrices are similar over C iff their characteristic polynomials are the same and their minimal polynomials are also the same.3. Two real matrices A and B are similar over
R iff they are similar over C .4. If an n
´ n real matrix A is diagonalizable over C , then it is triangulable over R iff it is diagonalizable over R .5. Let A be a 10
´ 10 complex matrix. If r(A) = 7 and r(A3) = 2, show that r(A2) = 4.6. Is the following data consistent for a 10
´ 10 complex A: r(A) = 7, r(A2) = 4, r(A3) = 3, and, r(A4 ) = 1?7. Let A be an n
´ n complex matrix. Let for some k, r(Ak) = p, and, r(Ak+2) = p-1. Prove that r(Ak+1) = p-1.
7. A Rank Based Determination of the Jordan Canonical Form
Let nk = nk(
l ) denote the number of k´ k Jordan blocks associated with an eigenvalue l in the JCF of a triangulable matrix A. If J is a p´ p Jordan block with eigenvalue zero, clearly r(J) = p-1, r(J2) = p-2, … , r(Jk) = p-k, … , r(Jp-1) = 1, and r(Jp) = r(Jp+1 ) = … = 0. Hence, if J(l ) is a p´ p Jordan block with eigenvalue l , we havep - r((J(
l )k) =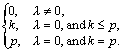
Summing this relation for all Jordan blocks we have: n-r(Ak) =
S k£ p knp(0)+S k>p pnp(0) = S i£ k ini(0)+kS I>k ni(0), k ³ 0. Note that for k = 0, r(Ak) = r(I) = n. It follows that for k ³ 0, r(Ak) - r(Ak-1) = nk+1(0) + nk+2(0) + nk+3(0) + …, so that d 2(r(Ak)) º r(Ak+1) - 2r(Ak) + r(Ak-1) = nk(0), k ³ 1. It follows that for each eigenvalue l of A, the number nk(l ) of k´ k Jordan blocks corresponding to l can be determined by the formula: nk(l ) = d 2(r((l I-A)k), k ³ 1.Moreover, we have the following result characterizing the sequence of ranks of powers of linear operators on finite dimensional vector spaces:
THEOREM. Let {rk}k
³ 0 be a non-incereasing sequence of non-negative integers. Then there exists a linear operator T on a vector space V of dimension n = r0 such that rk = r(Tk), k ³ 0 iff {rk} is convex, i.e., d 2(rk) º rk+1-2rk+rk-1 ³ 0, k ³ 1).PROOF: The necessity part follows from the formula
s 2(r(Tk)) = nk(0), k ³ 1. To prove the sufficiency, it is enough to construct an r´ r matrix J in Jordan canonical form for which r(Jk) = rk, k ³ 0. For this we choose the number nk = nk(0) of k´ k Jordan blocks corresponding to the eigenvalue 0 as nk = d 2(rk) ³ 0, k ³ 1. It follows that n1 + 2n2 + … + mnm = (r0 -2r1 +r2 ) + 2(r1 -2r2 +r3 ) + 3(r2 -2r3 +r4) + … + m(rm-1 -2rm +rm+1) = r0 + S 2£ k£ m-1 [(k-1)-2k+(k+1)]rk -(m+1)rm + mrm+1 = r0 – rm, where m is smallest such that rm = rm+1. Thus rm has to be the total size of the Jordan blocks corresponding to the eigenvalues that are non-zero. With the matrix J constructed as above, it is clear that r(Jm) = r(Jm+1) = rm. Moreover, for k < m, we have r(Jk) = nk+1 + 2nk+2 + … + (m-k)nm + rm = d 2(rk+1) + 2d 2(rk+2) + … + (m-k) d 2(rm) + rm = rk - (m-k+1)rm + (m-k)rm+1 + rm = rk, proving the result. #
PROBLEMS
1
. If N1 and N2 are n´ n nilpotent matrices and n £ 3, show that N1 and N2 are similar if and only if they have the same minimal polynomial. Is the result true for n´ n matrices with n ³ 4?2. Let T and S be two triangulable operators, the algebraic multiplicity each of their eigenvalues being less than four. Prove that T and S are similar iff they have the same minimal and the same characteristic polynomials.
3. Given that T is a linear operator on a vector space
V over a field F and that fT(x) = x9 -3x7 +3x5 –x3: (a) prove that T is triangulable, (b) find the dimension of V , (c) prove that each of the operators T, T+I and T-I is singular, (d) show that there are precisely twenty seven possibilities for the minimal polynomial pT(x) and that each of these is associated with a unique Jordan form of T, and, (e) find the Jordan form of T if pT(x) equals: (i) x3 - x, (ii) x4 – x2, (iii) x5 – x3, and, (iv) x7 - 2x5 + x3.4. How many possible Jordan forms are there for a complex matrix A with the characteristic polynomial fA(x) = (1+x)(1-x2)(1-x4)?
5. Find the Jordan form of the differentiation operator D on the space of real polynomials of degree less than or equal n. Also find the matrix of D with respect to each of the bases: {1, x, x2, … , xn}, and, {xn, Dxn, … , Dn-1xn , Dnxn}.
6. Find the Jordan form for the following matrices:
 .
.
7. If A is an n´ n complex matrix show that trace A = limx® ¥ x ln [xn/fA(x)].
8. The following 3´ 3 complex matrices A satisfy A3 + I = 0 and are mutually dissimilar:
![]() .
.
Are there any more such matrices? What is the total number of such dissimilar matrices? What is the total number of dissimilar n´ n complex matrices A such that An + I = 0?
9. Let n ³ 2 and 1 £ k < n be integers, and let N be an nxn matrix over a field F such that Nn = 0 but Nk ¹ 0. Prove that if m ³ n/k, N has no m-th root, i.e., that there is no n´ n matrix A such that Am = N.
10. Let N1 and N2 be n´ n nilpotent matrices, over a field F , of equal rank and having the same minimal polynomial. If n £ 6, prove that N1 and N2 are similar. Show that this is not true for n > 6.
11. Let T and S be triangulable linear operators, on a finite dimensional vector space V over a field F , having the same characteristic polynomial and the same minimal polynomial. If also for each c Î F , (T-cI) and (S-cI) have the same nullity and if each eigenvalue of A has algebraic multiplicity less than 7, prove that A and B are similar.
12. Prove that the Jordan form of the transpose of a Jordan form is the Jordan form itself.
13. Prove that similar matrices have the same Jordan form, and conversely.
14. If A is triangulable over a field G , show that A and A¢ have the same Jordan form in G . Deduce that A and A¢ over any field F are similar.
15. If A is similar to B and A¢ = P(A), where P is a polynomial, is it true that B¢ = P(B)?
16. If N is n´ n nilpotent matrix over a field F of characteristic zero, p and q are positive integers and a = p/q, prove that the truncated binomial series expansion T below satisfies Tq = (I+N)p:
T =(I+N)a = I + aN + [a(a-1)/2!]N2 + ... + [a(a-1)…(a-n+2)/(n-1)!]Nn-1.
17. Prove that every non-singular matrix A over an algebraically closed field G of characteristic zero, possesses an n-th root.
18. Show that iff c ¹ 0, the Jordan form of the matrix  is: J(l ) =
is: J(l ) = 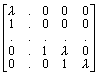 .
.
19. Which of the following statements is/are true? (a) The subset of R n´ n of matrices that are diagonalizable over R is dense in R n´ n, (b) The subset of R n´ n of matrices that are diagonlizable over C is dense in R n´ n, (c) The subset of C n´ n of matrices that are diagonalizable through a real matrix (i.e., C-1AC = D, C real) is dense in C n´ n , and, (d) The subset of C n´ n of matrices that are diagonlaizable over C is dense in C n´ n.
20. If A is a complex n´ n matrix, r (A) is its spectral radius and e > 0, there exists a matrix norm P × P such that P AP < r (A)+e .
21. Construct a linear operator T on some vector space V over a field F , of characteristic different from 2, such that pT(x) = (x-1)2(x+1)2 and fT(x) = (x-1)3(x+1)4. Describe the primary decomposition of the vector space under T and determine the projections on the primary components. Find a basis of V in which the matrix of T is in the Jordan form. Also find an explicit direct sum decomposition of the space into T-cyclic subspaces and write down the rational form of T and the associated invariant factors. Repeat the exercise with a field of characteristic 2.
22. Let A denote the matrix operator on R 8 given by
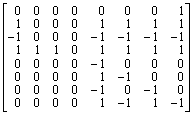 .
.
(a) Show that the diagonal entries of the Smith normal form of xI-A are: 1, 1, 1, 1, 1, 1, x2(x+1), and, x2(x+1)3. (b) Deduce the characteristic polynomial, the minimal polynomial and the invariant factors of A associated with its rational form. (c) Find the rational form of A. Find the Jordan form for each diagonal block in the rational form of A. (d) Find the cyclic decomposition of R 8 under T relative to W 0 = {0}. (e) Find the primary decomposition of R 8 under T and the projections on the primary components. Find cyclic decompositions of each primary component. (f) Find the Jordan form of A. Find a basis that puts A in the Jodan form. (g) Find a direct-sum decomposition of R 8 into T-cyclic subspaces other than those in the cyclic decomposition, if possible. (h) Show that A is similar to the following matrix B:
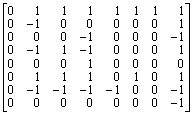 .
.
(i) Make an independent rank based determination of the Jordan form of B, starting with a determination of fB(x).
23. Let T be a triangulable operator on a vector space V over a field F . Prove that given the Jordan form of T it is possible to determine the rational form of T, and conversely. Would you suggest an algorithm for the same?