Chapter 8

GENERALIZED INVERSES

Definition of a g-Inverse

A generalized inverse (g-inverse) of an m´ n matrix A over a field F is an n´ m matrix G over F such that Gb is a solution of the system Ax = b of linear equations whenever b is such that this system is consistent. Conventionally, a g-inverse of A is denoted by A-. In the sequel the statement "G is an A-" means that G is a g-inverse of A. So does the statement "X Î A-". Thus, according to our usage, A- would, depending on the context, denote a particular g-inverse of A, a general g-inverse of A, or the class of all g-inverses of A.

Theorem. Let A be an m´ n matrix and A- an n´ m matrix. Put H = A-A and K = AA-. Then the following assertions are equivalent:

(i) A- is a g-inverse of A.

(ii) AA-A = A.

(iii) H = A- A is idempotent (H2 = H) and r(H) = r(A).

(iv) K = AA- is idempotent and r(K) = r(A).

(v) Ax = 0 iff for some z, x = (H-I)z.

(vi) x is a solution of consistent Ax = b iff for some z, x = A-b + (H-I)z.

(vii) Q¢ x has a unique value for all x satisfying Ax = b iff Q¢ H = Q¢ .

(viii) G is a g-inverse of A iff for some U, G = A- + U - A-AUAA-.

(ix) G is a g-inverse of A iff for some V and W, G = A- + V(I - AA-) + (I - A-A)W.

Proof: (i) Þ (ii): Ax = Az is consistent for arbitrary z. Hence if A- is a g-inverse of A, x = A-Az is a solution and so AA-Az = Az. As z is arbitrary AA-A = A.

(ii) Þ (i): Let Ax = b be consistent. Then b = Az for some z and A(A-b) = AA-Az = Az = b and so A-b is a solution. As b is arbitrary A- is a g-inverse of A.

(ii) Þ (iii): Premultiplying the relation in (ii) by A- the idempotence of H follows. Also A = AA-A Þ r(A) £ r(A-A) £ r(A) so that r(A-A) = r(A).

(iii) Þ (ii): H2 = H Û A-AA-A = A-A. r(A-A) = r(A) Þ R ((A-A)¢ ) = R (A¢ ) (column space, or range of A¢ ). Hence there exists a matrix C such that CA-A = A. Premultiplying the idempotence relation by C, AA-A = A.

(ii) Þ (iv): Post-multiplication in (ii) by A- shows that K is idempotent and r(A) = r((AA-)A) £ r(AA-) £ r(A) Þ r(AA-) = r(A).

(iv) Þ (ii): We have AA-AA-= AA- and R (AA-) = R (A). Hence, there exists a B such that AA-B = A Þ AA-AA-B = AA-A = AA-B = A.

(ii) Þ (v): (ii) Û A A-A = A. If x = (H - I)z = (A-A - I)z, then Ax = (AA-A - A)z = 0. Also, if Ax = 0, Hx = A-Ax = 0, so that with z = -x, x = (H - I)z.

(v) Þ (ii): (v) Þ " z, A(H - I)z = 0 Û (AA-A - A)z = 0 " z Û AA-A - A = 0 Û (ii).

(vi) Þ (ii): Ax = 0 is always consistent. Hence with y = 0, (vi) Þ (v) Þ (ii).

(ii) Þ (vi): Let x be a solution of a consistent Ax = b. By (ii), w = x - A-b is a solution of Aw = 0. By "(ii) Þ (v)", w = (H - I)z for some z so that x = A-b + (H - I)z for some z. On the other hand, if x = A-b + (H - I)z, by "(ii) Þ (v)", Ax = b.

(viii), (ix) Þ (i): By taking U, V, W = 0.

(ii) Þ (viii): If G = A- + U - A-AUAA-, then, using (ii), we have AGA = AA-A + AUA - AA-AUAA-A = AA-A + AUA - AUA = A and so by "(i) Û (ii)", G is a g-inverse of A. Conversely, if G is a g-inverse of A, choosing U = G - A-, A- + U - A-AUAA- = A- + G - A- - A-A(G - A-)AA- = G - A-(AGA)A- + A-(AA-A)A- = G - A-AA- + A-AA- = G, i.e., G has a required form.

(ii) Þ (ix): If G = A- + V(I - AA-) + (I - A-A)W, then AGA = AA-A + AV(I - AA-)A + A(I - A-A)WA = A + AVA - AVA + AWA - AWA = A and so G is a g-inverse. Conversely, let G be a g-inverse. With V = G - A- and W = GAA-, A- + V(I - AA-) + (I - A-A)W = A- + (G - A-)(I - AA-) + (I - A-A)GAA- = A- + G - GAA- - A- + A-AA + GAA- - A-AGAA- = G + A-AA - A-AGAA- = G + A-AA- - A-AA- = G, i.e., G has the required form.

(ii) Þ (vii): Q¢ x has a unique value for all x satisfying Ax = b Û (by (ii) Þ (vi)) that Q¢ (A-b + (H - I)z) is independent of z Û Q¢ (H - I)z = 0 " z Û Q¢ (H - I) = 0 Û Q¢ H = Q¢ .

(vii) Þ (ii): Let Q¢ be the i-th row ai of A. Then for all x with Ax = b, Q¢ x = aix = bi is independent of x. By (vii) Þ aiH = ai " i Û AH = A, i.e., AA-A = A, i.e., (ii).

Summarizing, we have established that (ii) Û each of (i) and (iii)-(ix), from which the equivalence of (i) to (ix) follows. #

For a complex matrix A, a general form of a g-inverse employing orthogonal projections is as follows:

Theorem. Let A Î C m´ n and A- Î C n´ m. Then the following assertions are equivalent:

(i) AA-A = A.

(ii) G is a g-inverse of A iff for some V and U, G = A- + V(I – PA ) + (I – PA*)U, where F = C and PA and PA* are the orthogonal projections on the ranges of A and A*, respectively.

Proof: (i) Þ (ii): If G = A- + V(I–PA) + (I–PA*)U, then AGA = AA-A + AV(I–PA)A + A(I–PA*)UA = A + AV(A-A) + APN (A)UA = A, since I - PA* = PN (A) (N (A) - null space of A) as follows: x Î N (A) Û Ax = 0 Û (Ax, y) = 0 " y Û (x, A*y) = 0 " y Û x ^ R (A*) (i.e., x is orthorgonal to R (A*)). Hence N (A) = R (A*)^ and so C n = N (A) Å ^ R (A ) (orthogonal direct sum). Hence I = PN (A) + PA*, I - PA* = PN (A).

Conversely, let G be a g-inverse of A. Choose V = G–A- and U = GPA – A-PA . Then, using I–PA* = PN (A), A- + V(I–PA) + (I-P A*)U = A- + (G–A-)(I–PA) + (I-PA*)(GPA – A-PA) = A- + G – GPA – A- + A-PA + GPA – A-PA - P A*GPA + P A*A-PA = G - P A*(G – A-)PA = G, as R ((G – A-)PA) Ì N (A) Þ G has the required form.

Taking V and U zero, (ii) Þ (i). #

 

PROBLEMS

1. Prove that any matrix is a g-inverse of a null matrix. Also show that if A is square and non-singular, A-1 is the only g-inverse of A.

2. (The most general form of a g-inverse). Let

denote the rank factorization of A where U and V are non-singular. Then A is a g-inverse of A if and only if

,

for some matrices X, Y and Z. Deduce that unless A is a square and invertible, there exist an infinity of g-inverses of A iff the scalar field is infinite (e.g., R or C).

3. Enumerate the total number of g-inverses of an m´ n matrix of rank r over the field Z p.

4. (The most general s.v.d. form of a g-inverse). Let

denote the singular value decomposition of A where U and V are unitary. Then A- is a g-inverse of A if and only if for some matrices L, M and N, it has the form

.

5. Prove that A is its own g-inverse iff there exist projections P, Q such that PQ = QP = 0 and P-Q = A.

6. If A is a generalized inverse of B, prove that B is a generalized inverse of A iff r(A) = r(B).

7. Let b, c be scalars and B, C g-inverses of A. Prove that bB+cC is a g-inverse of A iff b + c = 1.

8. Let Q be a projection (Q2 = Q) with R (Q) É R (A). Let A- be a g-inverse of A. Then G = A-Q is also a g-inverse of A. (Soln.: A(A-Q)A = AA-(QA) = AA-A = A. #)

 

Reflexive g-Inverse A-r

If G is a g-inverse of A such that A is a g-inverse of G, we call G a reflexive g-inverse of A. It is generically denoted by A-r and by definition satisfies: AA-rA = A (g-inverse) and A-rAA-r = A-r (reflexivity).

Theorem. A reflexive g-inverse A is characterized by: (a) AA-rA = A, and (b) r(A) = r(A-r).

Proof: If A is a reflexive g-inverse, r(A) £ r(A-r) £ r(A) (from the definition). Þ r(A) = r(A-r) and it being a g-inverse, AA-rA = A. Conversely, let these two conditions be satisfied. As A-r is a g-inverse A-rA is a projection with R (A-rA) Ì R (A-r). But, (A-r being a g-inverse) r(A-rA) = r(A) = r(A-r). Hence R (A-rA) = R (A-r) and so A-rA is a projection with range R (A-r). Then A-rAA-r = A-r, since the action of A-rA does not change the columns of A-r. #

 

PROBLEMS

1. (The most general form of a reflexive g-inverse). Given a rank factorization of A with B, C non-singular:

,

show that A-r is a reflexive g-inverse of A iff for some matrices X and Y:

.

2. Prove that A admits a unique reflexive g-inverse iff it is square and non-singular.

3. (The most general s.v.d. form of an A-r ). If a singular value decomposition of A with unitary U, V is

,

verify that A-r is a reflexive g-inverse of A if and only if, for some matrices L and M, it has the form

.

4. Prove that A is the only matrix which is a reflexive g-inverse of each reflexive g-inverse of A.

5. Let A-r be a reflexive g-inverse of A. If b Î R (A), prove that Ax = b admits a unique solution from R (A-r).

 

Least-Squares g-Inverse A-l

For a least-squares g-inverse A-l , x = A-lb minimizes (b-Ax)*(b-Ax), i.e., ||b-AA-lb||2 £ ||b-Ax||, " x. If this condition holds, automatically A-l becomes a g-inverse: for, if Ax = b is consistent, the ‘least-squares’ must be zero. Thus, A-l is a least-squares g-inverse iff it is a g-inverse and AA-l = PA, i.e., AA-lA = A and (AA-l)* = AA-l. Note AA-lA = A Þ AA-l is a projection and r(AA-l) = r(A) and so AA-l is a projection onto R (A). Then if AA-l is also Hermitian it becomes an orthogonal projection and so "AA-lA = A and AA-l = PA". Hence:

Theorem. A least squares g-inverse A-l of A is characterized by: (a) AA-lA = A, & (b) (AA-l)* = AA-l.

Theorem. Let A- be a g-inverse of A. Then G is a least square g-inverse A-l of A iff for some W

G = A-PA + (I – PA*)W = A-PA + PN (A) W.

Proof: (I - PA*)Wb Î N (A) and A-PAb is a least squares solution of Ax = b. Hence A-PA + (I - PA*)W is an A-l. Let G be an A-l. Being a g-inverse G = A- + V(I – PA) + (I - PA*)U, for some U & V. Now G = PA*G + (I - PA*)G = PA*GPA + (I - PA*)G, as PA*G = A+ = PA*GPA, G being an A-l. So, G = PA*A-PA + (I - PA*)G = A-PA + (I - PA*) (G – A-PA) = A-PA + (I - PA*)W, where W = G – A-PA. #

 

Generalized M-least-squares g-inverse A-l(M): If M is a p.d. matrix for any b, by definition, x = A-l(M)b minimizes (b-Ax)*M(B-Ax) = ||M1/2b-M1/2Ax||22. Hence, A-l(M) could be related to (M1/2A)–l by (M1/2A)-l M1/2 = A-l(M) Û (M1/2A)-l = A-l(M)M-1/2. Hence A-l(M) is characterized by: (a) M1/2 AA-l(M)M-1/2M1/2A = M1/2A Û AA-l(M)A = A, and (b) (M1/2AA-l(M)M-1/2)* = M1/2AA-l(M)M-1/2 Û (AA-l(M))*M = MAA-l(M):

Theorem. For a p.d. M, A-l(M) is an M-LS g-inverse of A iff (A) AA-l(M)A = A, and (B) (AA-l(M))*M = M(AA-l(M)).

 

PROBLEMS

1. If G Î A-, prove that GG*Î (A*A)- iff G Î A-l.

2. Let A be m´ n and B and C n´ m complex matrices. Verify that 2B-C and 2C-B are A-l iff B and C are A-l.

3. (The most general s.v.d. form of an A-l). Let the singular value decompostion of A be given by

,

where U, V are unitary and L is a positive diagonal matrix. Then A-l is a least-squares g-inverse of A iff for some M, N

.

4. Prove that GPA is an A-l if and only if G is an A-. (Hint: LS solutions of Ax = b are the solutions of Ax = PAb).

 

Minimum Norm g-Inverse A-m

G is called a minimum-norm g-inverse of A if for all consistent systems Ax = b, x = Gb provides the solution with minimum norm. A minimum norm g-inverse of A is denoted by A-m. Obviously an A-m is a g-inverse of A. Any b such that the system Ax = b is consistent has form b = Az, for some z. Then, if x is a solution of Ax = b, since the minimum norm solution is x - PN (A)x = (I - PN (A) )x = PA*x, A-m is characterized by A-mAz = PA*z, " z, i.e., A-mA = PA*. But, A-m being a g-inverse, A-mA is a projection and so it is an orthogonal projection if it is Hermitian. Conversely, if A-m is an A- and A-mA is Hermitian, from (A-mA)* = A*(A-m)* = A-mA, and r(A-mA) = r(A) = r(A*), Þ R (A-mA) = R (A*). Consequently, A-mA is the orthogonal projection onto R (A*). We have, therefore, proved that

Theorem. A minimum norm g-inverse A-m is characterized by:

(a) AA-mA = A, and (b) (A-mA)* = A-mA Û (c) A-mA = PA*.

Lemma. PA*A- is an A-m.

Proof: If Ax = b is consistent, x = A-b is a solution. As A-b = PA*A-b + PN (A)A-b, (PA*A-)b is the minimum norm solution. #

 

Lemma. Let A-m be a minimum-norm g-inverse of A. Then G = A-m + V(I – PA) = A-m + VPN (A*), where V is any nxm matrix, is also a minimum-norm g-inverse.

Proof: If Ax = b be consistent, b Î R (A), and so Gb = A-m b + V(I-PA)b = A-mb is a minimum-norm solution. #

Theorem. Let A- be any fixed g-inverse of A. Then, G is a minimum-norm g-inverse A-m of A iff for some W: G = PA*A- + W(I-PA) = PA*A- + WPN (A*).

Proof: By the previous two lemmas, G = PA*A- + VPN (A*) is a minimum-norm g-inverse of A. Conversely, let G be an A-m.Then G is a g-inverse and so G = A- + V(I-PA) + (I-PA*)U, for some U and V. Now, as G is an A-m, G = GPA + GPN (A*) = PA*GPA + GPN (A*) = PA*A-PA + A-PN (A*) + VPN (A*) + (I-PA*)UPN (A*) = PA*A- - PA*A-PN (A*) + {A + V + (I-PA*)U}PN (A*) = PA*A- + WPN (A*) , where W = {A + V + (I-PA*)U - PA*A-}. #

Generalized Minimum N-Norm g-Inverse A-m(N): For a positive definite n´ n N, A-m(N) is such that A-m(N)b has minimum N-norm Ö (x*Nx) out of all solutions of a consistent Ax = b. Rewriting, Ax = b Û AN-1/2N1/2 x = b Û By = b, where B = AN-1/2 , y = N1/2x. Then B-m and A-m(N) are related by N-1/2B-m = A-m(N) , i.e., B-m = N1/2A-m(N). Hence, since B-m is characterized by BB-mB = B Û AN-1/2N1/2A-m(N)AN-1/2 = AN-1/2 Û AA-m(N)A = A, and (B-mB)* = B-mB Û (N1/2 A-m(N)AN-1/2)* = N1/2A-m(N)AN-1/2 Û (A-m(N)A)*N = N(A-m(N)A), it follows that A-m(N) is characterized by:

Theorem. A-m(N) is a min. N-norm g-inv. of A iff (A) AA-m(N)A = A, & (B) (A-m(N)A)*N = N(A-m(N)A).

 

PROBLEMS

1. (The most general s.v.d. form of an A-m). Let

,

denote the singular value decomposition of A where U and V are unitary. Then A-m is a minimum-norm g-inverse of A if and only if it has the form

,

for some matrices L and N, where 0 stands for a zero matrix.

2. A-mPA is another min. norm g-inverse of A. (Hint: If Ax = b is a consistent system, b = Az for some z. Hence (A-mPA)b = A-mPAAz = A-mAz = A-mb is a min. norm solution. #)

 

Moore-Penrose Inverse A+

The Moore-Penrose inverse A+ of A Î C m´ n, generically the minimum norm least-squares g-inverse applied on the right hand side of a system Ax = b is to give least-squares solution of minimum norm. Observe that the minimum norm-least-squares solution of the system is obtained by orthogonally projecting b on R (A), solving the consistent system Ax = PAb, and then projecting the solution vector x orthogonally on R (A*), the orthogonal complement of N (A). Since any two least squares solutions differ by an element of N (A), their orthogonal projections on R (A*) are identical, whence it follows that a minimum norm least-squares solution exists and is unique. As each of the above operations is linear the minimum norm least squares solution is obtainable by the action of a linear operator on the right hand side vector, namely, PA*A-PAb. It follows that A+ exists and moreover that, for any choice of A-, A+ = PA*A-PA:

Theorem. A+ exists, is unique and if A- is any g-inverse of A, PA*A-PA = A+.

Proof: Since A-PA Î A-l , x = PA*A-PAb is the minimum norm least squares solution of the system Ax = b. Hence, PA*A-PA = A+. The unicity of the minimum norm least squares solution implies that if G is another minimum norm least squares g-inverse then Gb = A+b, for all b Þ G = A+, i.e., A+ is unique. #

Theorem. A+ is characterized by: (a) AA+A = A, (b) A+AA+ = A+, (c) (AA+)* = AA+, (d) (A+A)* = A+A; or equivalently by: (e) AA+ = PA, (f) A+A = PA* and (g) A+AA+ = A+.

Proof: If a matrix A+ satisfies (a)-(d), we show that A+ is the Moore-Penrose inverse: For this (a) Þ (AA+)2 = AA+ and r(AA+) = r(A) Þ R (AA+) = R (A). By (c), (AA+)* = AA+. Þ AA+ = PA Û ||b - AA+b|| £ ||b – Ax||, " x. Also, (a) Û (A+A)2 = A+A and r(A+A) = r(A) = r(A*). By (d), A*(A+)* = (A+A)* = A+A* and these two together imply that A+A = PA*. Thus, since A+ due to (a) is a g-inverse of A, PA*A+PAb is the min. norm-least-squares solution. But PA*A+PA = (A+A)A+(AA+) = A+AA+ = A+ (by (a) and (b)). Thus, A+ satisfying (a)-(d) is the min. norm-least-squares g-inverse.

Conversely, if A+ is the min. norm least squares solution then it is an A-l Û (a) & (c), as well as an A-m Û (a) & (d). Now A+b is a l.s. solution of Ax = b. Hence the systems Ax = A(A+b) and Ax = b have identical l.s. and therefore identiacal min. norm l.s. solutions. Hence A+(AA+)b = A+b, " b Þ A+AA+ = A+, i.e., (b).

Finally, (e) Û (a) & (c), and (f) Û (a) & (d) and therefore, (e)-(g) Û (a)-(d). #

 

Generalized More-Penrose inverse A+MN (N-minimum norm M-least-squares g-inverse): Let ||x|| = Ö (x*Nx) and ||b - Ax|| = Ö ((b – Ax)*M(b – Ax)), M, N being m´ m and n´ n positive definite matrices. The min. N-norm M-least squares g-inverse with respect to these norms is denoted by A+MN. If N1/2 , M1/2 denote the square roots of N and M, the system Ax = b, with x ® N1/2x, b ® M1/2 b, reduce to the system to (M1/2AN-1/2)(N1/2x) = M1/2b. Then A+MN = N-1/2(M1/2AN-1/2)+M1/2, so that (a) (M1/2AN-1/2) (M1/2AN-1/2)+ (M1/2AN-1/2) = (M1/2AN-1/2) Û (M1/2AN-1/2) (N1/2A+MNM-1/2) (M1/2AN-1/2) = (M1/2AN-1/2) Û AA+MNA = A; (b) (M1/2AN-1/2)+ (M1/2AN-1/2) (M1/2AN-1/2)+ = (M1/2AN-1/2)+ Û (N1/2A+MNM-1/2) (M1/2AN-1/2) (N1/2A+MNM-1/2) = (N1/2A+MNM-1/2) Û A+MNAA+MN= A+MN; (c) ((M1/2AN-1/2) (M1/2AN-1/2)+)* = (M1/2AN-1/2) (M1/2AN-1/2)+ Û ((M1/2AN-1/2) (N1/2A+MNM-1/2))* = (M1/2AN-1/2) (N1/2A+MNM-1/2) Û (AA+MN)M = M(AA+MN); and (d) ((M1/2AN-1/2)+ (M1/2AN-1/2))* = (M1/2AN-1/2)+ (M1/2AN-1/2) Û ((N1/2A+MNM-1/2) (M1/2AN-1/2))* = (N1/2A+MNM-1/2) (M1/2AN-1/2) Û (A+MNA)*N = N(A+MNA). Thus we have the existence, uniquness and the following characterization of A+MN:

Theorem. A+MN is characterized by: (a) AA+MNA = A, (b) A+MNAA+MN = A+MN, (c) (AA+MN)M = M(AA+MN), and (d) (A+MNA)N = N(A+MNAA+MN).

 

PROBLEMS

1. Writing A+MN = A+l(M)m(N), show that: (i) (A*)-m(M) = (A-l(M-1))*; (ii) (A+MN)+NM = A; (iii) (A+MN)* = (A*)+ N-1 M-1;

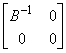(iv) A+MN = N-1A*MA(A*MAN-1A*MA)-A* M; (v) A-l(M) = (A*MA)-A*M; (vi) A-m(N) = N-1A*(AN-1A*)-; (vii) if B is r´ r non-singular, r = r(A) &, then is an A-r and 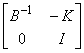is an A- of maximum rank equalling min{m, n}an A- of maximum rank equalling min{m,n};

(viii) TFAE: (a) G is an A-l, (b) AGA = A, (AG)* = AG, (c) AG = PA, (d) (AG)*A = A;

(ix) TFAE: (a) G is an A-m, (b) AGA = A, (GA)* = GA, (c) GA = PA*, (d) A(GA)* = A;

(x) G is A+ iff G is A-l, A-m, and A-r.

2. Let A = BC be a rank factorization of A, where B is m´ r, C is r´ n and r = r(A). Show that (a) B-l is uniquely given by B-l = (B*B)-1B*, (b) C-m is uniquely given by C-m = C*(CC*)-1, & (c) C-mB-l = C*(CC*)-1(B*B)-1B* = A+, the Moore-Penrose inverse of A.

3. Let A be m´ n, B m´ r and C r´ n, where r = r(A). Show that C*(B*AC*)-1B* = A+, the Moore-Penrose inverse of A iff (a) the column space of B equals the column space of A and (b) the row space of C equals the row space of A.

4. Let A be an m´ n matrix. Show that we can find a unitary H (use Householder rotations) such that r(A) equals the number of non-zero rows of HA. Use elementary row operations to get a non-singular G such that GHA has orthonormal non-zero rows. Show that the minimum-norm least-squares solution of Ax = b is given by x+ = (GHA)*GHb, and that accordingly, A+ = (GHA)*GH.

5. Prove that the following results hold for any choice of g-inverses: (a) A(A*A) -A*A = A and A*A(A*A)-A* = A; (b) A necessary and sufficient condition that BA-A = B is that R (B’) Ì R (A’) (Û R (B*) Ì R (A*)); (c) if B and C be non-null, then BA-C is invariant for any choice of A- iff R (B’) Ì R (A’) and R (C) Ì R (A); (d) A(A*A) -A* is hermitian and invariant for any choice of the g-inverse (A*A) -.

6. G is a g-inverse of A iff I - GA = pN (A)|· , a projection on N (A), null space of A along whatever (· ) subspace.

7. G is a g-inverse of A iff AG = pR (A)|· .

8. G is a g-inverse of A iff for some g-inverse A- of A, G has the form: G = A- + V(I - pR (A)|.) + pN (A)|.W.

9. Let A = E diag [H,0] F be a rank factorization (i.e., r(H) = r(A), E, F, H - non-singular) of A. Then G is an A- iff G = 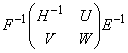, and it is reflexive iff G =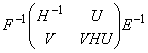, for some U, V, W.

10. (The s.v.d. form of an A+). Let A = denote the singular value decomposition of A where U and V are unitary. Prove that A+ is given by A+ = 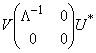.