Chapter 9

COURANT-FISCHER MIN-MAX THEOREMS

A Variational Characterization of Eigen-Values

Let A be Hermitian n´ n and (l , x) be an eigen-pair of A. Then, using the standard inner product l (x,x) = (Ax,x) = (x,A^*x) = (x,Ax) = l ^*(x,x), (l ^* denoting complex conjugate of l ), and so, as x ¹ 0, Þ l = l ^*, i.e., l is real. Hence the eigen-values values of a Hermitian matrix are real. Let the n eigen-values of A (counted after algebraic multiplicities) be indexed according to l ₁ ³ l ₂ ³ l ₃ ³ … ³ l _n and let u¹, u², u³, ... , uⁿ be the corresponding orthonormal eigen-vectors (obtained e.g., via unitary diagonalization). A variational characterization of eigen-values of a Hermitian matrix is as follows:

Theorem 1. Let U₀ = {0} and U_k = span {u¹,u², ... ,u^k} º <u¹,u², ... ,u^k>. Then

(a) l _k = max_{0¹ x^ Uk-1} (Ax,x)/(x,x), k = 1, 2, ... , n; &

(b) l _k = min_{0¹ xÎ Uk} (Ax,x)/(x,x), k = 1, 2, ... , n.

Proof: 0 ¹ x ^ U_k-1 Û x = S _{k£ j£ n} a _ju^j, with at least one a _j non-zero. Hence

max₀¹ x^ Uk-1 (Ax,x)/(x,x) = maxa _j S _k£ j£ n l _j|a _j|²/S _k£ j£ n |a _j|² = l _k,

(which is obtained e.g., for the vector x = u^k). Similarly, 0 ¹ x Î U_k Û x = S _{k£ j£ n} a _ju^j, with at least one a _j ¹ 0. Hence, min_{0¹ xÎ Uk} (Ax,x)/(x,x) = mina _j S _{k£ j£ n} l _j|a _j|²/S _{k£ j£ n} |a _j|² = l _k, (the min. being attained e.g., by x = u^k). #

Remark. If A is real symmetric, u^j’s could be taken real (by orthogonal diagonalization) and since with x = S _{k£ j£ n} a _ju^j, (Ax,x)/(x,x) = S _{k£ j£ n} l _j|a _j|²/S _{k£ j£ n} |a _j|², it follows that all the values taken by the Rayleigh-quotient (Ax,x)/(x,x) for complex x are also attained for real vectors (note the presence of |a|²). Hence, in Theorem 1, and so in the resuts below, when A is real-symmetric the results hold with the confinement to real subspaces, i.e., working only w.r.t. R ⁿ.

Indeed, Theorem 1 heavily depends on certain particular subspaces and so is not suitable for many applications (see, e.g., the proof of Theorem 3 below). This difficulty is avoided through the following Courant-Fischer min-max theorem:

Theorem 2. (R. Courant & E. Fischer Min-Max Theorem). Let W stand for an arbitrary k-dimensional subspace of C . Let A be Hermitian. Then for k = 1, 2, 3, ... , n

(I) l _k = min_Wk-1 max_{0¹ x^ Wk-1} (Ax,x)/(x,x),

(II) l _k = min_Wn-k+1 max_{0¹ xÎ Wn-k+1} (Ax,x)/(x,x),

(III) l _k = max_Wn-k min_{0¹ x^ Wn-k} (Ax,x)/(x,x),

(IV) l _k = max_Wk min_{0¹ xÎ Wk} (Ax,x)/(x,x).

Proof: Let m _k = min_Wk-1 max_{0¹ x^ Wk-1} (Ax,x)/(x,x). Restricting "min" to W_k-1 = U_k-1 only, by Theorem 1(a), m _k < l _k. For the reverse inequality, with x = S _{1£ j£ n} a _ju^j, restricting the set on which "max" is taken

m _k ³ min_Wk-1 max_{0¹ x^ Wk-1,xÎ Uk} (Ax,x)/(x,x) = min_Wk-1 max_{0¹ x^ Wk-1,xÎ Uk} S _{1£ j£ k} l _j|a _j|²/S _{1£ j£ n} |a _j|² ³ min_Wk-1 max_{0¹ x^ Wk-1,xÎ Uk} l _k = l _k,

provided we can show that {x : 0 ¹ x ^ W_k-1 , x e U_k} is non-empty. For this, suppose W_k-1^ and U_k have no non-zero element in common. Then Z = W_k-1^ + U_k = W_k-1^ Å U_k is a direct sum. Now, Z being a subspace of C ⁿ, n ³ dim Z = dim W_k-1^ + dim U_k = n-(k-1) + k = n+1, a contradiction. This establishes (I).

Noting that (I) Û (II) and (III) Û (IV), it remains to prove (III) only. For this, put

n _k = max_Wn-k min₀¹ x^ Wn-k (Ax,x)/(x,x).

Again, restricting W_n-k’s to U_k^ only, by Theorem 1(b), one has: n _k ³ l _k. Next, with x = S _{1£ j£ n} a _ju^j,

n _k £ max_Wn-k min_{0¹ x^ Wn-k,Uk-1} (Ax,x)/(x,x) = max_Wn-k min_{0¹ x^ Wn-k,Uk-1} S _{k£ j£ n} l _j|a _j|²/S _{1£ j£ n} |a _j|² £ max_Wn-k min_{0¹ x^ Wn-k,Uk-1} l _k = l _k,

provided again we can show that W_n-k^ and U _k-1^ have a non-zero intersection. But if the intersection is {0}, Y = W_n-k^ + U _k-1^ is a direct sum of dimension equaling k + n-(k-1) = n + 1, again a contradiction. This completes the proof of Courant-Fischer min-max theorem. #

Corollary. Let W _k stand for an arbitrary subspace of dimension ³ k and w _k for that of dimension £ k. Let A be hermitian m´ n. Then for 1 £ k £ n,

(I) l _k = min {max {x^*Ax/x^*x : 0 ¹ x ^ w _k-1} : w _k-1};

(II) l _k = min {max {x^*Ax/x^*x : 0 ¹ x Î W _n-k+1} : W _n-k+1};

(III) l _k = max {min {x^*Ax/x^*x : 0 ¹ x ^ w _n-k} : w _n-k};

(IV) l _k = max {min {x^*Ax/x^*x : 0 ¹ x Î W _k} : W _k}.

Proof: By decreasing a subspace we allow more x's to become orthogonal to it. Thus in (I) the max does not decrease while in (III) the min does not increase. Similarly, by increasing a subspace we allow more elements to become available so that in (II) the max does not decrease, while in (IV) the min does not increase. Hence the additional subspaces do not change the min in (I) and (II) and the max in (III) and (IV). #

Corollary. If A is n´ n hermitian matrix and B Î C ^{n´ k}, 1 £ k £ n-1, then: inf_B sup_B*x=0 x^*Ax/x^*x = l _k+1, and, sup_B inf_B*x=0 x^*Ax/x^*x = l _n-k.

Proof: The column space of B is atmost k-dimensional. Hence the results follow, respectively from (I) and (III) of the previous corollary. #

Theorem 2 may be used to prove the following Sturmian separation theorem:

Corollary. (Sturmian Separation Theorem). Let A be n´ n Hermitian and A_k its k-th principal sub-matrix (composed of the intersection of the first k rows and columns). Then the eigenvalues of A_i+1 interlace those of A_i, i.e.,

l _k+1(A_i+1) £ l _k(A_i) £ l _k(A_i+1), 1 £ k £ i; 1 £ i £ n-1.

Proof: Since A_i’s themselves are Hermitian, it is sufficient to prove the inequalities for i = n-1. Let (W_k)ⁿ simultaneously stand for an arbitrary k-dimensional subspace of C ⁿ of elements with the n-th component x_n = 0 and an arbitrary k-dimensional subspace of C ^n-1 . By Theorem 2(II),

l _k+1 = min_Wn-k max_{0¹ xÎ Wn-k} (Ax,x)/(x,x) £ min_(Wn-k)n max_{0¹ xÎ (Wn-k)n} (Ax,x)/(x,x) £ min_(Wn-k)n max_{0¹ xÎ (Wn-k)n} (A_n-1x,x)/(x,x) £ min_{(W(n-1)-k+1)n} max_{0¹ xÎ (W(n-1)-k+1)n} (A_n-1x,x)/(x,x) £ l _k(A_n-1).

Also, by Theorem 2(IV), l _k(A_n) = max_Wk min_{0¹ xÎ Wk} (Ax, x)/(x, x) ³ max_(Wk)n min_{0¹ xÎ (Wk)n} (Ax,x)/(x,x) ³ max_(Wk)n min_{0¹ xÎ (Wk)n} (A_n-1x, x)/(x, x) = l _k(A_n-1). #

Corollary. (Poincare Separation Theorem). Let A be n´ n and B n´ k subunitary (B^*B = I). Then:

l _i(B^*AB) £ l _i(A), 1 £ i £ k;

l _k-j(B^*AB) ³ l _n-j(A), 0 £ j £ k-1.

Proof: Augment B with n-k additional columns to get a n´ n unitary matrix V. Then l _i(V^*AV) = l _i(A), as A and V^*AV are similar. If we put V^*AV = C, then C_k = B^*AB. Hence

l _i(C_k) = l _i(B^*AB) £ l _i(C_k+1) £ l _i(C_k+2) £ … £ l _i(C_n) = l _i(A).

Similarly, l _k-j(B^*AB) = l _k-j(C_k) ³ l _k+1-j(C_k+1) ³ l _k+2-j(C_k+2) ³ … ³ l _n-j(C_n) = l _n-j(A). #

Aliter: Use l _i = max {min {(Ax,x)/(x,x) : x Î W_i}: W_i}. Restricting W_i’s to C ^k Þ l _i(A) ³ l _i(B^*AB), 1 £ i £ k. Similarly, using l _n-j = min {max {(Ax,x)/(x,x) : x Î W_j+1}: W_j+1} and restricting W_j+1’s to C ^k, 0 £ j £ m-1, Þ l _n-j(A) £ l _k-j(B^*AB). #

Theorem. Let S stand for a set of k mutually orthogonal non-zero n´ 1 vectors v¹, v², ... , v^k and let A be a hermitian n´ n matrix with eigenvalues l _i’s in decreasing fashion. Then:

sup_S {S _{1£ i£ k} ((vⁱ)^*Avⁱ)/((vⁱ)^*vⁱ)} = S _{1£ i£ k} l _i;

inf_S {S _{1£ i£ k} ((vⁱ)^*Avⁱ)/((vⁱ)^*vⁱ)} = S _{n-k+1£ i£ k} l _i.

The "sup" and the "inf" are attained respectively for the vectors u¹, u², ... , u^k and u^n-k+1, u^n-k+2, ... , uⁿ, where uⁱ’s are the orthonormal eigenvectors of A corresponding to the eigenvalues l _i.

Proof: Without loss of generality, vⁱ’s may be assumed to be orthonormal. Let vⁱ = S _{1£ j£ n} c_iju^j. Then

S _{1£ i£ k} ((vⁱ)^*Avⁱ)/((vⁱ)^*vⁱ) = S _{1£ i£ k} (S _{1£ p£ k} c_ipu^p)^*(S _{1£ j£ k} l _jc_iju^j) = S _{1£ i£ k} (S _{1£ p£ k} l _p|c_ip|²) = S _{1£ p£ k} l _p(S _{1£ i£ k} |c_ip|²) = S _{1£ p£ k} l _p(S _{1£ i£ k} |(vⁱ, u^p)|²) = S_{1£ p£ k} l _{pa p},

say. Note that 0 £ a _p £ 1, they being the sum of squares of projection coefficients of u^p w.r.t. vⁱ’s orthonormal and also that S _{1£ p£ n} a _p = S _{1£ i£ k} ||vⁱ||² = k. The required estimates follow from this. #

In the following result, ||A||_F denotes the Frobenius norm given by ||A||_F = S _i (S _j |a_ij|²)^1/2 = (tr A^*A)^1/2.

Theorem. Let A be p.d. and C stand for any matrix of rank k. Then inf_C ||A-C||_F = (l _k+1² + ... + l _n²)^1/2, and the infimum is attained when C = l ₁u¹(u¹)^* + ... + l _ku^k(u^k)^*.

Proof: Since the Frobenius norm is invariant under unitary transformations, let U = (u¹ | u² | ... | uⁿ) be a unitary diagonalizer of A, uⁱ’s being normalized eigenvectors corresponding to the eigenvalues l _i’s in decreasing order. Then, U^*AU = diag (l _i, l ₂, ... , l _n). A general matrix C can be written as C = UBU^* and it is of rank k iff B is of rank k. Then ||A-C||_F² = S _{1£ i£ n} |l _i – b_ii|² + (S _{i¹ j} |b_ij|²). Since r(B) = k, not more than k of b_ii’s can be non-zero. Hence the first sum on the r.h.s. above is ³ l _k+1² + ... + l _n², showing that Inf_B ||A-B||_F ³ (l _k+1² + ... + l _n²)^1/2. Moreover the lower bound on the r.h.s. is attained if b_ij = 0, i ¹ j, and b_ii = l _i , 1 £ i £ k, the B thus obtained is diag (0, 0, ... , l _k+1, ... , l _n) and is of rank k. Thus a C for which the bound is attained is given by C = UBU^* = l ₁u¹(u¹)^* + ... + l _ku^k(u^k)^*, as stated. #

Let’s recall that the inertia of a matrix is defined by In(A) = (p (A), n (A), d (A)), p , n , and d denoting the number of eigenvalues of A with positive, negative and zero real parts, respectively, counted after their algebraic multiplicities. The Sylvester’s inertia theorem says that a non-singular conjugate linear transformation does not change the inertia of a hermitian matrix and can be proved easily by using the Courant-Fischer min-max theorem:

Sylvester's Inertia Theorem. If C is non-singular and H is hermitian, In(C^*HC) = In(H) = (p (H), n (H), d (H)), p , n , and d denoting the number of eigenvalues with positive, negative and zero real parts, respectively, counted after their algebraic multiplicities).

Proof: With x ¹ 0 and y = Cx, we have (C^*HCx, x)/(x, x) = ((Hy, y)/(y, y)) ((Cx, Cx)/(x, x)), so that l _n(C^*C)((Hy, y)/(y, y)) £ (C^*HCx, x)/(x, x) £ l ₁(C^*C)((Hy, y)/(y, y)). Taking max over k-dimensional subspace W_k’s of min over x Î W_k, we get the inequality: l _n(C^*C)l _k(H) £ l _k(C^*HC) £ l ₁(C^*C)l _k(H), called Ostrowsky's quantitative formulation of the Sylvester’s inertia theorem. Since C is non-singular, C^*C > 0 (i.e., p.d.) and so has positive eigenvalues. Hence l _k(H) and l _k(C^*HC) have the same sign for all k from which the Sylvestor’s inertia theorem follows. #

Exercise. Prove that Sylvester's inertia theorem is equivalent to each of the following statements:

(a) If P > 0 and H is hermitian then In (PH) = In (H).

(b) If AH > 0 and H is hermitian then IN A = in H.

Generalization of Haynsworth Inertia Sum Formula: If H = (H_ij)_{1£ i,j£ 2} is a partitioned hermitian matrix with H₁₁ non-singular, In H = In H₁₁ + In (H₂₂ –H₁₂^*(H₁₁)^-1H₁₂), which is known as Haynsworth inertia sum formula. If H is possibly singular but the column space M (H₁₁) É M (H₁₂), we have the generalization: In H = In H₁₁ + In (H₂₂ –H₁₂^*(H₁₁)^-H₁₂), for any choice of g-inverse (H₁₁)^-.

Proof: If M (H₁₁) É M (H₁₂), for any choice of H₁₁^-, H₁₂ = H₁₁(H₁₁)^-H₁₂. By Sylvester's inertia theorem

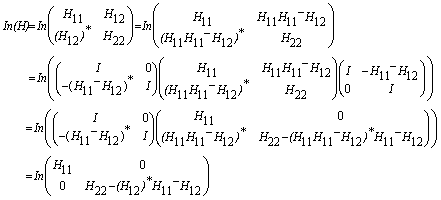
and the result follows. #

Remark. If H₁₁ is non-singular then M (H₁₁) É M (H₁₂), so that the Haynsworth inertia sum formula is a special case of the above result. Moreover, when M (H₁₁) É M (H₁₂), H₁₂ = H₁₁C for some C and then In H = In H₁₁ + In (H₂₂ –C^*H₁₁C).

Given's Method for a Hermitian Matrix

In this method for A real-symmetric (hermitian) matrix, we use a succession of similarity transformations based on the Jacobi planar rotations to first turn the matrix into a tri-diagonal real-symmetric (hermitian) matrix similar to the given one. The procedure ia a variant of the iterative Jacobi method and is based on the rows and columns

(2, 3), (2, 4), ... , (2, n),

(3, 4), ... , (3, n),

………...,

(n-1, n),

to turn the elements in the following positions to zero

(1, 3), (1, 4), ... , (1, n),

(2, 4), ... , (2, n),

……......,

(n-2, n).

In this sequence the earlier created zeros continue to remain zeros and at the end of the process after atmost (n² -3n+2))/2 similarity transformations the real-symmetric (hermitian) matrix A is turned into a tri-diagonal real-symmetric (hermitian) matrix. Subsequently, the method of Sturm sequences is used to locate the eigenvalues of the matrix.

Note that the iterative Jacobi method is based on (i, j)-th rows and columns to turn (i, j) and (j, i)-th entries to zero, whereas here in the Given’s method the same effect is produced by using (i+1, j)-th rows and columns. The advantage is that the previously created zeros do not revive and the process terminates in n-2 steps; the disadvantage is that one ends up with a tri-diagonal, rather than a diagonal matrix.

One could also use Householder reflections for the tri-diagonalization: in which for 1 £ i £ n-2, for the i-th column one reflects the (n-i)-component column vector of bottom (n-i)-entries in the direction of the first unit vector in K ^n-I, along with the corresponding conjugate row operations on the last (n-i)-entries of the i-th row. At the i-th stage the earlier processed i-1 rows and columns remain unchanged.

Eigenvalues of a Tridiagonal Hermitian Matrix

.

We consider the non-degenerate case where each c_j is non-zero. If any c_j is zero the eigenvalues of A are the eigenvaues of the j-th principal submatrix A_j and the (n-j)´ (n-j) submatrix of A obtained by deleting the first j-rows and the first j-columns of A, to which the method can be applied separately. Putting f₀(x) = 1 and f_k(x) = |xI-A_k|, 1 £ k £ n, we have f_k+1(x) = (x-b_k+1)f_k(x) - |c|²f_k-1(x), 1 £ k £ n-1. From this it follows that at a zero of f_k(x), i.e., at an eigenvalue x of A_k, f_k(x) and f_k+1(x) have opposite signs. This implies that the eigenvalues of A_k+1 strictly interlace the eigenvalues of A_k. If f_k(x) and f_k+1(x) have opposite signs, it signifies that A_k+1 has one more eigenvalue on the right of x than A_k. Hence the number N(x) of sign changes of the sequence {f₀(x), f₁(x), f₂(x), … , f₃(x), ... ,f_n(x)}, equals the number of eigenvalues of A on the right to x, which is the number of eigenvalues of A lying in the open interval (x, ¥ ). It follows that: N(a)-N(b) equals the number of eigenvalues of A lying in the interval (a,b]. If f (b) ¹ 0, it equals the number of eigenvalues in (a,b). If f_n(a) ¹ 0, it equals the number of eigenvalues in [a,b]. Thus using different a’s and b’s all the eigenvalues of A could be located.