Chapter 10

INEQUALITIES IN MATRIX THEORY

The Volume of an m-Dimensional Parallelepiped

For an m-dimensional rectangular parallelepiped in R ^m , the lengths of whose mutually perpendicular sides are l₁, l₂, ... , l_m, the volume (for m = 3, area for m = 2 and the so-called hyper-volume for m > 3) is defined to be P _{1£ i£ m} l_i. Here the length is the Euclidean length of a vector side. If the vectors defining concurrent sides of a rectangular parallelepiped are the unit vectors e_i , i = 1, 2, ... , m, obviously the volume equals 1 = |det (e₁ | e₂ | ... | e_m)| and if the vectors are c_ie_i , it equals |c₁c₂…c_m| | = |det (c₁e₁ | c₂e₂ | ... | c_me_m)|. This formula remains valid even if the vectors are not orthogonal, i.e., if the concurrent sides are v₁, v₂, ... , v_m, the volume of the parallelepiped is given by V = |det (v₁ | v₂ | ... | v_m)|, for, if P_i is the orthogonal projection on the orthogonal complement of span {v₁, v₂, ... , v_m}, then det (v₁, v₂, ... , v_m) = det (v₁, P₁v₂, P₂v₃, ... , P_m-1v_m) and the column vectors on the r.h.s. are concurrent sides of a rectangular parallelepiped of the same volume as that of the original parallelepiped. (Two volumes corresponding to the same base and the same height are equal!)

Another useful formula for the volume which may be derived from the above is

V² = det [(v_i, v_j)]₁£ i,j£ m = det [(v₁ | v₂ | ... | v_m)^*( v₁ | v₂ | ... | v_m)],

where (v_i, v_j) is the inner product of v_i and v_j. The formula

V² = det [(a_i, a_j)]₁£ i,j£ m,

where a₁, a₂, ... , a_k are the concurrent side vectors of a parallelepiped in any inner product space (real or complex) and V is the volume of this k-dimensional parallelepiped and where the dimension of the space need not be k or even finite, is a generalized version of the above formula. The proof is analogous to that of the first formula for

det [(a_i, a_j)]₁£ i,j£ k = det [(P_i-1a_i, P_j-1a_j)]₁£ i,j£ k = det [diag [(P_i-1a_i, P_i-1a_i)]₁£ i£ k],

and the last expression is the product of squares of sides of a rectangular parallelepiped of the same volume as the original parallelepiped.

Change of Variables in Multiple Integrals

Let x, y Î K ^m. Consider ò _Dy f(y) dV_y where y ranges over the volume of an n-dimensional region D_y. Let the vector variable y be related with x according to y = y(x), where y is a continuously differentiable vector function of x. Let the Jacobian of the transformation be denoted by

.

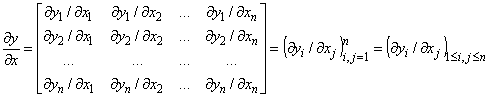As y ranges over D_y, let x run over D_x. An infinitesimal parallelepiped in the region D_x with concurrent sides (du₁, du₂, ... , du_n) corresponds to an infinitesimal parallelepiped in the region D_y with concurrent sides given by (dv₁, dv₂, ... , dv_n) = ((¶ y/¶ x)du₁, (¶ y/¶ x)du₁, ... , (¶ y/¶ x)du_n) = (¶ y/¶ x)(du₁, du₂, ... , du_n). Thus ò _Dy f(y) dV_y = ò _Dy f(y) |det (dv₁, dv₂, ... ,dv_n)| = ò _Dx f(y(x)) |det (¶ y/¶ x)| |det (du₁, du₂, ... ,du_n)|. Hence

ò _Dy f(y) dV_y = ò _Dy f(y(x)) |det(¶ y/¶ x)| dV_x is the required change of variable formula in multiple integrals.

In the sequel, while considering surfaces and volumes, unless otherwise stated the matrices under consideration are real.

Surface and Volume of a Hyper-Sphere

Let |A| ¹ 0 and consider the multiple integral . If we put y = Ax, then, x = A^-1y, and so

.

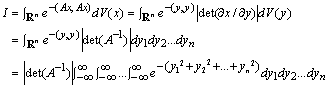But as , it follows that

I = p ^n/2/|det A| = p ^n/2/|l ₁(A) l ₂(A) ... l _n(A)|,

where l _i(A), i = 1, 2, ... , n are the n eigenvalues of A. Hence

.

Corollary 1. Let B be positive definite. Then

.

Proof: Let A = Ö B. Then, (Bx, x) = (Ax, Ax) and l _i(A) = Ö l _i(B), i = 1 (1) n. #

Corollary 2. Let A_n(r ) denote the surface area of the n-dimensional sphere S_n(r ) of radius r . Then

A_n(r ) = 2p ^n/2r n-1/G (n/2).

Proof: Taking B = I, the identity matrix

.

Thus, A_n(1) = 2p ^n/2/G (n/2). Since A_n(r ) = r ^n-1A_n(1), the result follows. #

Remark: Note that A₂(r) = 2p r, the circumference of a circle with radius r, A₃(r) = 2p ^3/2r² /[(1/2)p ^1/2] = 4p r², the area of the surface of sphere of radius r, which are the familiar formulae. Note that A₁(r) = 2, the number of the end points of the line segment [-r, r]!

Corollary 3. The volume V_n(r ) of the n-sphere of radius r is given by

.

Proof: V_n(r) = ò _0¥ A_n(r)dr = ò _0¥ [2p ^n/2r^n-1/G (n/2)] dr = 2p ^{n/2r n}/[nG (n/2)] = [p ^n/2/G (n/2 + 1)] r ⁿ. #

Remark: V₁(r) = (Ö p /(Ö p /2))r = 2r, the volume of 1-sphere of radius one (i.e., the length of the interval {x : |x| < r}), V₂(r) = (p /G (2))r² = p r², area inside a circle of radius r, and V₃(r) = p Ö p /((3/2)(1/2)Ö p )r³ = (4/3)p r³, the familiar formula for the volume of a sphere of radius r.

Corollary 4. Let A and B be positive definite and 0 < q < 1. Then, |q A + (1-q )B| > |A|q |B|^1-q .

Proof: By Corollary 1, and using Holder's inequality with 1/p = l , 1/q = 1-l , we have

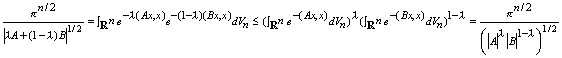
from which the desired inequality follows. #

The Volume of an n-Dimensional Ellipsoid

Let the ellipsoid be (Ax, x) < 1, where A is n´ n positive definite. Let A = UDU^*. Let dx stand for the

infinitesimal volume element in R ⁿ. Then the volume of the ellipsoid is

V_A = ò _(Ax,x)<1 dx = ò _(Dy,y)<1 dy = ò ₍Ö Dy,Ö Dy)<1 dy = |D|^-1/2ò _(z,z)<1 dz = p ^n/2|D|^-1/2/G + 1) = p ^n/2|A|^-1/2/G (n/2+ 1) = p ^n/2|l ₁(A)l ₂(A) … l _n(A)|^-1/2/G (n/2 + 1) = [G (n/2 + 1)]^-1ò R _n e^-(Ax,x)dx.

The restriction of the ellipsoid (Ax, x) < 1, to the orthogonal complement of a set of k-linearly independent vectors u₁, u₂, ... , u_k is given by the conditions: (Ax, x) < 1, (x, u_i) = 0, 1 £ i £ k and constitutes an n-k dimensional ellipsoid. For, without loss of generality we may assume u_i, 1 £ i £ k, orthogonal, and complete these to an orthonormal basis u_i, 1 £ i £ n. Let U = (u₁ | u₂ | ... | u_n), a column partitioned form. Then x = UU^*x and with V = (u_k+1 | u_k+2 | ... | u_n) for y Î < u₁, u₂, ... , u_k > ^ , y = VV^*y and so the above restriction conditions are equivalent to y Î < u₁, u₂, ... , u_k > ^ , 1 > (AVV^*y, VV^*y) = ((V^*AV)V^*y, V^*y) and V being of rank n-k, z = V^*y runs over an n-k dimensional space as y has form y = Vt, t running over R ^n-k and moreover V^*AV is an (n-k)´ (n-k) positive definite matrix.

The volume of the largest m-dimensional section of an ellipse is to be obtained in the sequel.

Principal Semi-Axes of a Section of an Ellipsoid

The lengths of principal semi-axes of the ellipsoid E _n : (Ax, x) < 1 are 1/Ö l _n(A), 1/Ö l _n-1(A), ... , 1/Ö l ₁(A), written in non-increasing order of magnitude. For, letting A = Udiag(l _n(A), l _n-1(A), ... , 1/l ₁(A))U^*, the unitary transformation y = U^*x transforms the ellipsoid to (diag (l _n(A), l _n-1(A), ... , 1/l ₁(A)) y, y) < 1, i.e.,

.

Moreover, the volume of the ellipsoid is given by

.

Let V_n-m be an n-m dimensional subspace of R ⁿ and let E _m denote the restriction of E _n to the orthogonal complement of V_n-m . Then E _m is described by {(Ax, x) < 1 : x ^ V_n-m}. Let the lengths of the principal semi-axes of E _m be denoted, in non-decreasing order of magnitude, by 1/Ö m _m(A), 1/Ö m _m-1(A), ... , 1/Ö m ₁(A). Let X_m = V_n-m^ . By the Courant-Fischer min-max characterization:

l _k = min_Wn-k+1max₀¹ xÎ Wn-k+1x^*Ax/x^*x £ min_Wn-k+1Ì Xmmax₀¹ xÎ Wn-k+1x^*Ax/x^*x = m _m+1-(n-k+1) = m _m-n+k.

Hence m _m-n+k ³ l _k, so that 1/Ö m _m £ 1/Ö l _n, 1/Ö m _m-1 £ 1/Ö l _n-1, … , 1/Ö m ₁ £ 1/Ö l _n-m+1, implying thereby that the lengths of semi-axles of restriction of an ellipse are never larger than the corresponding lengths of the original ellipse. The max-min characterization, on the other hand gives:

m _k(A) = max_WkÌ Xm min₀¹ xÎ Wk x^*Ax/x^*x £ max_Wk min₀¹ xÎ Wk x^*Ax/x^*x = l _k(A),

i.e., 1/Ö m _k(A) ³ 1/Ö l _k(A). These inequalities lead us to:

V_m £ p ^m/2 /[Ö (l _n-m+1 …l _n-1l n)G (m/2 + 1)],

V_m ³ p ^m/2 /[Ö (l _ml m-1…l ₁)G (m/2 + 1)].

Corollary: The largest and the smallest volumes of m-dimensional sections of an ellipse (Ax,x) < 1 are, respectively, given by:

maxE _m V_m = p ^m/2 /[Ö (l _n-m+1 …l _n-1l n)G (m/2 + 1)],

minE _m V_m = p ^m/2 /[Ö (l _ml m-1…l ₁)G (m/2 + 1)].

Proof: The foregoing implies that the r.h.s.’s in the above give, respectively, an upper bound and a lower bound. But these bounds are attained for the m-dimensional sections, respectively, given by:

º { x ^ u_m+1, u_m+2, ... , u_n | x^*Ax < 1}

& º { x ^ u₁, u₂, ... , u_n-m | x^*Ax < 1}. #

For A positive definite, let us define |A|_k = l _{nl n-1} ... l _n-k+1, which is the product of the k smallest eigenvalues of A.

Theorem. Let V_k denote a k-dimensional subspace of R ⁿ. Then for a real positive definite matrix A,

,

where ‘dx’ stands for the infinitesimal volume element in V_k (i.e., is the restricted Lebesgue measure) and the ‘max’ is over the class of all k-dimensional subspaces.

Proof: Let the ellipsoid E_k(r ; V_k) = {x : (Ax, x) < r , x Î V_k} have volume V_k(r ) = r ^k/2V_k(1). Then, as

,

the result follows from the expressions for the maximum and the minimum volumes of a k-dimensional section of an ellipse in the previous corollary. #

Corollary (Ky Fan). If A, B are real p.d. matrices, |q A+(1-q )B|_k > (|A|_k)q (|B|_k)^1-q , 0 £ q £ 1, 1 £ k £ m.

Proof: Using Holder's inequality with 1/p = q , 1/q = 1-q , the result follows from previous theorem. #

Corollary (Ky Fan). For a real symmetric (hermitian) matrix A, let S_k(A) denote the sum of the smallest n-k+1 eigen values of A: S_k(A) = l _n(A) + l _n-1 (A) + ... + l _k(A). Then

S_k(q A + (1-q )B) ³ q S_k(A) + (1-q )S_k(B), 1 £ k £ n, 0 £ q £ 1.

Proof: For all e > 0 sufficiently small, I + e A and I + e B are p.d. and l _i(I + e A) = 1 + e l _i(A), l _i(I + e B) = 1 + e l _i(B) and l _i(q (I + e A) + (1-q )(I + e B)) = 1 + e l _i(q A + (1-q )B), as e being positive the non-increasing order of the eigenvalues is preserved. By the previous corollary applied to I + e A and I + e B, we have: P _i=n(-1)k (1 + e l _i(q A + (1-q )B)) ³ (P _i=n(-1)k (1 + e l _i(A)))q (P _i=n(-1)k (1 + e l _i (B)))^1-q . It follows that: 1 + e S _i=n(-1)k l _i(q A + (1-q )B)) ³ 1 + e q S _i=n(-1)k l _i(A) + e (1-q )S _i=n(-1)k l _i (B) + O(e ²). Canceling 1, dividing by e (>0) and taking limit as e ® 0, the result follows. #

Corollary (Ky Fan). If T_k(A) = l ₁(A) + l ₂(A) + ... + l _k(A) and A, B are real symmetric (Hermitian)

T_k(q A + (1-q )B) £ q T_k(A) + (1-q ) T_k(B), 1 £ k £ n, 0 £ q £ 1.

Proof: S_k(-A) = -(l ₁(A) + l ₂(A) + ... + l _n-k+1(A) = -T_n-k+1(A), and the result follows from the previous corollary. #

Aliter: Tr(A) is the sum of all the eigenvalues of A and Tr(q A + (1-q )B) = q Tr(A) + (1-q )Tr(B). The result follows after subtracting the inequality in the previous corollary from this equality. #

Theorem (Ky Fan). Let A be p.d. and R = {(z₁, z₂, ... , z_n-k+1)} : (z_i, z_j) = d _ij , 1 £ i, j £ n-k+1}, the collection of all (n-k+1)-ples of orthonormal vectors. Then: l _{1l 2} ... l _n-k+1 = maxR det ((z_i, Az_j))_{1£ i,j£ n-k+1}, and l _{nl n-1} ... l _k = minR det ((z_i, Az_j))_{1£ i,j£ n-k+1}. (The proof is valid for complex p.d. matrices.)

Proof: First note that the max on the right hand side is attained when z_i is taken as an eigen vector corresponding to the eigen value l _i , 1 £ i £ n-k+1, in a unitary diagonalization of A. Similarly, the min on the right hand side is attained when z_i is taken as the eigen vector corresponding to the eigen value l _n-i+1, 1 £ i £ n-k+1. Next, ((z_i, Az_j))' = ((Az_j, z_i)) = (z₁ | z₂ | ... | z_n-k+1)^*A(z₁ | z₂ | ... | z_n-k+1) = B^*AB, say, where the column partitioned matrix B = (z₁ | z₂ | ... | z_n-k+1) is sub-unitary. Hence by the Poincaré separation theorem l _i(B^*AB) £ l _i(A), 1 £ i £ n-k+1, and l _n-k+1-j(B^*AB) ³ l _n-j(A), 0 £ j £ n-k. Hence, with D = det((z_i, Az_j)) = det(B^*AB) = l ₁(B^*AB)l ₂(B^*AB) ... l _n-k+1(B^*AB), as the eigenvalues of B^*AB and A are positive, we have D £ l ₁(A)l ₂(A) … l _n-k+1(A) and D ³ l _n(A)l _n-1(A) … l _k(A) proving thereby that maxR _D £ l ₁(A)l ₂(A) … l _n-k+1(A) and minR _D ³ l _n(A)l _n-1(A) … l _k(A), which, since the right hand expressions are attained, proves the theorem. #

Theorem. If A is positive definite, then |A| £ a₁₁ a₂₂ ... a_nn. (The result is valid also for the complex case, as the second proof will show.)

Proof: p ^n/2/Ö |A| = ò R _n e^-(Ax,x) dx = ò R _n exp [-S _{1£ i,j£ n} a_ijx_jx_i] dx = ò R _n exp [-S _{1£ i,j£ n} s _{is j}a_ijx_jx_i] dx, by changing the variable x to -x , where s _k = 1 if k ¹ 1 and s _k = -1 if k = 1. Taking the arithmetic mean (A.M.)of the last two integrals and using A.M. ³ G.M., the geometric mean, we have

p ^n/2/Ö |A| ³ ò R _n exp [-a₁₁x₁² -S ₂£ i,j£ n a_ijx_jx_i] dx.

Similarly, replacing x₂ by –x₂, and so on upto x_n-1 by –x_n-1 and at each stage proceeding analogously we end up with p ^n/2/Ö |A| ³ ò R _n exp [-S _{1£ i£ n} a_iix_i²] dx = p ^n/2/Ö ( a₁₁ a₂₂ ... a_nn), from which the result follows. #

Aliter: We can write: 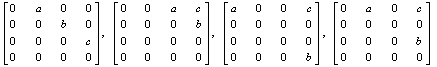, say. Then B is positive definite and so B^-1 is positive definite and hence the matrix (B_ij) of co-factors of B is also positive definite. If M_ji denotes the (j, i)-th minor of A, expanding by the 1^st column

,

as (B_ij) is positive definite. Hence

,

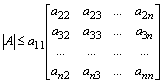and the result follows by induction over n. #

Note: This proof is valid also when A is complex p.d. matrix (or even p.s.d. when, of course, the result is trivial).

Corollary. Let B be a real square matrix. Then: |B| < P _{1£ i£ n} (S _{1£ k£ n} b_ik²). (Hadamard's inequality)

Proof: |B| = |BB'| and (BB')_ii = S _{1£ k£ n} b_ik² , 1 £ i £ n. #

Application of Poincare Separation Theorem to Ellipsoids

An m-dimensional section of an n-dimensional ellipsoid E _n = {x Î R ⁿ : (Ax, x) = 1}, obtained by restricting its hyper surface to an m-dimensional subspace W_m is given by E _m = {x Î W_m : (Ax, x) = 1}. Let {u₁, u₂, ... ,u_m} be an orthonormal basis of W_m. Then if x Î W_m, x = a ₁u₁ + ... + a _mu_m for some vector a = (a ₁, ... , a _m) Î R ^m. Thus, x = (u₁ | u₂ | ... | u_m)a = Ua , say. Note that for the n´ m U we have U^*U = I, i.e., U is sub-unitary. Thus E _m = {a Î R ^m : (AUa , Ua ) = 1} = {a Î R ^m : (U^*AUa , a ) = 1}. Hence the k-th principal semi-axis of E _m is given by a_k^(m) = (l _m-k+1(U^*AU))^-1/2. By the Poincaré separation theorem, therefore a_k^(m) £ a_k⁽ⁿ⁾ and a_m-k+1^(m) £ a_n-k+1⁽ⁿ⁾ i.e., a_n-k+1^(m) £ a_m-k+1^(m) £ a_m-k+1⁽ⁿ⁾, providing an easier approach than before. #