Chapter 11
PERRON-FROBENIUS THEORY OF NON-NEGATIVE MATRICES
Non-Negative Matrices and Vectors
A real m´ n matrix A = (aij) is called a non-negative matrix if its entries are non-negative (i.e., aij > 0) and it is called a positive matrix if aij > 0, 1 £ i £ m, 1 £ j £ n. If n or m equal one we have the case of vectors. Thus the zero and the identity matrices and the standard unit vectors are examples of non-negative matrices. A Hilbert matrix is a positive matrix. For any m´ n complex matrix A, |A| denotes the matrix whose entries are the magnitudes of the corresponding entries in A. Thus |A| is a non-negative matrix and similarly |x| is a non-negative vector. To denote that A is a non-negative matrix we write A ³ 0. If A is a positive matrix we write A > 0. If B-A ³ 0, we write B ³ A, and if B-A > 0 that B > A. One should not confuse a posistive matrix with a positive definite, and a non-negative matrix with a non-negative definite (positive semi-definite) matrix.
PROBLEMS
1. Prove that A ³ 0 iff whenever x ³ y, Ax ³ Ay.
2. Prove that A ³ 0 iff whenever x ³ 0, Ax ³ 0.
3. If A ³ 0 is n´ n and S1£ i£ n aij < 1, 1 £ j £ n, or, S1£ j£ n aij < 1, 1 £ i £ n, show that I-A is invertible with its inverse is non-negative. If, in addition A > 0 prove that (I-A)-1 > 0.
4. If 1 > aij > 0, S 1£ i£ n aij £ 1 for all j, with strict inequality for at least one j, show that B = A2 satisfies: S 1£ i£ n bij < 1, for all j and hence that (I-A)-1 > 0.
5. If A > 0 and l > r (A), show that |l I-A| > 0.
6. The inverse of a positive definite matrix is positive definite. Contrast it with the fact that the inverse of a positive matrix can never be positive, unless the matrix is 1´ 1.
7. Let y be fixed. Prove that x ³ y implies Ax ³ y for all x iff A ³ 0 and Ay ³ y.
8. Prove that Ay ³ y for every y iff A = I.
9. Find n if the square of each real n´ n matrix is to be non-negative.
10. If Am ³ 0, m ³ 2 and A is real, is it a must that A ³ 0?
11. Do A ³ 0 and 0 ³ A2 imply that A = 0?
12. Prove that every non-negative matrix is unstable.
13. If Am > 0, for all m ³ 2, is it necessary that A > 0?
14. Let A > 0. Prove that {Am}m³ 1 converges iff r (A) < 1.
Perron's Theorem on Positive Matrices
Theorem (Perron). If A > 0, (i) the spectral radius r (A) of A is positive and is a simple eigenvalue of A, (ii) r (A) is associated with a positive eigenvector, (iii) no eigenvalue of A, other than r (A), is associated with an eigenvector x ³ 0, (iv) if B ³ A and B ¹ A, then r (B) > r (A) and (v) no other eigenvalue of A is of magnitude r (A).
Proof: Define r = sup l ³ 0 : Ax ³ l x, for some 0 ¹ x ³ 0}. It is clear that r > 0 and that there is a vector 0 ¹ x > 0, say, such that Ax ³ rx . If Ax ¹ rx , 0 ¹ y = Ax - rx ³ 0, so that Ay > 0. Hence Ay ³ e Ax for some e > 0. Putting z = Ax , Az > (r+e )z, contradicting the definition of r. Hence Ax = rx . Since Ax > 0 we have x > 0. Thus r is an eigenvalue of A and x is an associated positive eigenvector.
If (l , x) is an eigen-pair of A, |l ||x| £ A|x| and so |l | £ r. It follows that r = r (A) so that r (A) is positive and is an eigenvalue of A. Further, if |l | = r (A), we have r (A)|x| £ A|x|, and if r (A)|x| ¹ A|x|, applying A to the difference vector, again we get a contradiction to the maximality of r = r (A). Hence r (A)|x| = A|x| > 0. It follows that |x| > 0 and x = eif z, for some z > 0 so that l z = Az = r (A)z, implying that l = r (A). Hence l (A) is the only eigenvalue of A of modulus r (A) and an associated eigenvector has to be a scalar multiple of a positive vector.
If r (A) does not have its algebraic multiplicity equal to its geometric multiplicity, using the Jordan canonical form of the matrix C = A/r (A), it follows that Ck is unbounded as k ® ¥ and hence so is Ckx = x , a contradiction. Hence the algebraic multiplicity of the eigenvalue r (A) equals the number of linearly independent eigenvectors associated with it.
We have already seen that any eigenvector associated with r (A) is a scalar multiple of a positive vector. Hence if the geometric multiplicity of r (A) exceeds 1, it has another positive eigenvector z which is not a scalar multiple of x. Let b = min { x j/z j : 1 £ j £ n}. Then h = x - b z ¹ 0 is a non-negative eigenvector associated with r (A) which has at least one component zero, a contradiction. Hence the geometric multiplicity of r (A) is one.It follows that r (A) is a simple eigenvalue of A (i.e., r (A) is an eigenvalue of algebraic multiplicity one) and that it corresponds to a positive eigenvector.
Next, let x ³ 0 be an eigenvector of A. With the vector x as before, let a = min { xj/x j : 1 £ j £ n}. Then xp = a x p, for some p. If l is the eigenvalue associated with x, we have l x = Ax ³ a Ax = a r (A)x , from which, as Ax > 0, there follow l > 0, x > 0, a > 0 and moreover, comparing the p-th components on the two sides of the inequality l xp ³ a r (A)x p = r (A)xp, so that l ³ r (A). It follows that no eigenvalue of A other than r (A) is associated with a non-negative eigenvector.
Finally, let B denote a matrix obtained from A by increasing some of its entries. Then Bx > r (A)x , with strict inequality in at least one component so that as before, from B(Bx ) > r (A)Bx , we conclude that r (B) > r (A). This completes the proof of the theorem. #
Corollary. If A > 0, 0 ¹ x ³ 0 and Ax ³ |l |x, then |l | £ r (A) and if |l | = r (A) then x > 0 and Ax = r (A)x.
Proof: From the definition of r in the proof of Perron's theorem, we have |l | £ r (A). If |l | = r (A) and Ax ¹ |l |x, the maximality of r is contradicted by one more application of A. Hence |l |x = Ax and the positivity of x follows. #
PROBLEMS
1. Let A > 0. Let T(A) denote the set of positive l for which there exists a positive vector x such that Ax £ l x and let S(A) denote the set of non-negative l for which there exists a non-negative vector x such that Ax ³ l x. Prove that r (A) = max S(A) = min T(A).
2. Prove that r (A) ³ r (B) if A ³ B ³ 0.
3. If A is a real matrix and A2 > 0, prove that A has a unique eigenvalue l of the magnitude r (A) and that l is real. Is the result true if Am > 0 for some m > 2.
4. Let A > 0 be n´ n. If {e1, e2, ... , en} is the standard ordered basis of Rn, prove that r (A) = max {min {(ei'Ax)/(ei'x) : 1 £ i £ n} : 0 ¹ x ³ 0}, and also that r (A) = min {max {(ei'Ax)/(ei'x) : 1 £ i £ n} : 0 ¹ x ³ 0}.
5. If A is a real n´ n matrix with positive off diagonal elements, prove that ed A > 0 for all d > 0. Hence for such an A, deduce that the eigenvalue l of A with largest real part is real and simple and is associated with a positive eigenvector. Moreover, it also has the following variational characterizations:
l
= max {min {(ei'Ax)/(ei'x) : 1 £ i £ n} : 0 ¹ x ³ 0} = min {max {(ei'Ax)/(ei'x) : 1 £ i £ n} : 0 ¹ x > 0}.6. Find a matrix A such that |A| > 0, but r (A) = 0 and r (A) is a multiple eigenvalue of A associated with a positive eigenvector.
7. Find the eigenvalues and eigenvectors of A = ![]() and |A|.
and |A|.
Irreducible Matrices and Directed Graphs
One may enquire as to what happens if in the statement of the Perron's theorem the hypothesis A > 0 is replaced by A ³ 0. The following examples illustrate the various situations: Of the matrices
A = ![]() , B =
, B =![]() , C =
, C = ![]() , D =
, D = ![]() , E =
, E = ![]() , F = diag (A, B, C, D).
, F = diag (A, B, C, D).
(a) A violates (ii) and (v) since r (A) = 1 is a double eigenvalue and increasing (1,2)-th element does not increase r (A). (b) B violates (i), (ii), (iii) and (v) as r (A) = 0 and is a double eigenvalue not associated with any positive eigenvector and increasing (1,2)-th entry does not change r (A). (c) C violates (iii)-(v). (d) D violates (vi) only, as the eigenvalues of A are -1 and 1. (e) E does not violates any of (i)-(vi). (f) The block diagonal matrix F whose diagonal blocks are the matrices in (a)-(d) fails to satisfy (i)-(vi).
The way out of the confusion and an insight into the eigen-structure of non-negative matrices is provided by a notion of reducibility through similarity transformations by permutation matrices obtained by permuting the order of the unit vectors in the standard ordered basis {e1, e2, ... , en}: Let A be an n´ n square matrix. One of the simplest similarity transformations on A is of type PAP', where P is a permutation matrix, i.e., each row, as well as column, of A contains precisely one non-zero entry and this entry is 1. If pi s (i) = 1 and pij = 0 if j ¹ i, 1 £ i £ n, (i.e., pij = d s (i) j ) s is a permutation on the set of indices {1, 2, ... , n}. Pre-multiplication by P brings s (i)-th row in the place of i-th row and post-multiplication by P takes j-th column to the position of s (j)-th column, 1 £ i, j £ n. Similarly, pre-multiplication by P' takes i-th row to the position s (i)-th row and post-multiplication by P' brings s (j)-th column to the position of the j-th column, 1 < i, j < n. Since any permutation can be written as a product of transpositions, an interchange of two columns of a matrix followed by an interchange of the corresponding rows of the matrix constitutes such a similarity transformation and any similarity transformation by a permutation matrix can be affected by a sequence of such interchange operations.
It may also be noted that if A is the matrix of a linear operator T with respect to the standard ordered basis B = {e1, e2, ... , en} and if B (s ) = {es (1), es (2), ... , es (n)}, then [T]B (s ) = [B]B (s ) [T]B [B(s )]B = PAP', with P as in the above. Thus PAP' is the matrix of T with respect to the permuted standard ordered basis whose members are the respective columns of the matrix P'.
A square matrix A is called reducible if there exists a permutation matrix P such that
PAP' = ![]() ,
,
where 0 is a null matrix (i.e., with all entries zero) and E and G are square. The problem of determining the eigen- values of a reducible A then simplifies to that of determining the eigenvalues of the lower order matrices E and G. A matrix that is not reducible is said to be an irreducible matrix.
For an n´ n A, taking n distinct points G1, G2, ... , Gn (called nodes) in the plane (say) and connecting Gi with Gj by a one-way path (called a loop if i = j, and a directed edge if i ¹ j, both of which may be termed as paths of unit length, or more appropriately, unit steps) with an arrow on it directed from Gi to Gj if aij ¹ 0, 1 £ i, j £ n, one gets the so-called directed graph G = G(A) of the matrix A. G is said to be strongly connected if it is possible to travel from any node to any node strictly along the one-way paths in G. (Note that jumping from a node to another is prohibited and looping about a node is of no consequence unless n = 1!). Since the effect of a permutation transformation PAP' is just to permute the nodes, G(A) is strongly connected iff G(PAP') is strongly connected. (Note that if P = Ps is a permutation matrix, as (i)s (j) is the (i,j)-th element of PAP'.)
Lemma. A is irreducible iff G(A) is strongly connected.
Proof: If A is reducible PAP' =![]() , for a permutation matrix P. Let E be m´ m. Then, for i > m, the graph G(PAP') has no path from the i-th node Gi to the node Gj for j £ m. Hence G(PAP') is not strongly connected. Consequently, so is G(A).
, for a permutation matrix P. Let E be m´ m. Then, for i > m, the graph G(PAP') has no path from the i-th node Gi to the node Gj for j £ m. Hence G(PAP') is not strongly connected. Consequently, so is G(A).
Conversely, if G(A) is not strongly connected for some pair (i, j) there is no path from the node Gi to the node Gj. Consider the set S of all indices k such that there is no path from Gi to Gk. If S has m elements, take a permutation P that maps S onto {1, 2, ... , m}. Then PAP' has the form PAP' =![]() , where E is m´ m, so that A is reducible. #
, where E is m´ m, so that A is reducible. #
Lemma. A n´ n non-negative (n ³ 2) is irreducible iff (I+A)n-1 > 0.
Proof: Consider the graph G(A). We note that an (i, j)-th element of the l-th power Al of A is positive iff there is a path of length l connecting the node Gi with the node Gj (i.e., there exist indices k(1) , k(2) , ... , k(l-1) such that aik(1), ak(1)k(2), ... , ak(l-1)j > 0). Since (I+A)n-1 = S 0£ l£ n-1 n-1ClAl, the result follows from the previous lemma. #
Corollary. If A ³ 0 is irreducible, 0 ¹ x ³ 0 and Ax ³ |l |x, then |l | £ r (A) and if |l | = r (A) then x > 0 and Ax = r (A)x.
Proof: With C = (I+A)n-1 , where A is n´ n, we have C > 0, and moreover Cx ³ (1+|l |)n-1x. Hence the result is clear from the corollary to the Perron's theorem.
PROBLEMS
1. If A-B is diagonal, prove that A is irreducible iff B is.
2. If A, B ³ 0, show that A+B is irreducible if A or B is.
3. A real matrix A is called monotone if Ax ³ 0 Þ x ³ 0. If A-1 exists and is real, prove that A is monotone iff A-1 ³ 0.
4. If an irreducible A has aij £ 0, i ¹ j and S 1£ j£ n aij ³ 0, for all i, where in the latter strict inequality holds for at least one i, prove that A is monotone.
5. A square matrix A is called diagonally dominant if for all i, |aii| ³ S j¹ i |aij|. If A is real, irreducible, diagonally dominant and has positive diagonal and non-positive off-diagonal elements, show that A-1 exists and is positive.
6. Prove that a monotone matrix is invertible.
7. If A is diagonally dominant with |aii| > S j¹ i |aij| for at least one i, prove that r (D-1(A-D)), r ((A-U)-1U) < 1, where D is the diagonal and U the strictly upper-triangular part of A, provided that A is irreducible. (The result may be interpreted as saying that the Jacobi and the Gauss-Seidel iterative methods for solving Ax = b, defined respectively by Dx(k+1) = -(A-D)x(k) +b and (A-U)x(k+1) = -Ux(k) +b, (k ³ 0) converge for such an A for any b and any initial vector x(0).)
8. Which of the following matrices are irreducible:
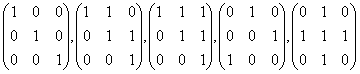 ?
?
The Perron-Frobenius Theorem
Theorem (Perron-Frobenius). If A ³ 0 is irreducible, (i) the spectral radius r (A) of A is positive and is a simple eigenvalue of A, (ii) r (A) is associated with a positive eigenvector, (iii) no eigenvalue of A, other than r (A), is associated with a non-negative eigenvector, and (iv) if B ³ A and B ¹ A, then r (B) > r (A).
Proof: If A is 1´ 1, the Perron's Theorem applies. Hence let n ³ 2 and let A be n´ n and U denote the n´ n matrix whose every entry is 1. Then for e > 0, Ae = A+e U > 0 and to it we can apply Perron's theorem. Let x e be the positive eigenvector of Ae of unit norm corresponding to the eigenvalue r (Ae ). Passing to the limit as e ® 0, it follows that r (A) = lime ® 0 r (Ae ) is an eigen value of A. Let x denote a limit point of the sequence {x e } as e ® 0. Then x is an associated eigenvector of norm 1 and x ³ 0. Let C = (I+A)n-1 . Then C is positive and x ³ 0 is an eigenvector of C. Hence, by Perron's theorem, x > 0 (and is associated with the eigenvalue r (C). By the irreducibility, at least one entry in A is non-zero, so that Ax = r (A)x implies that r (A) > 0. Let l 1, l 2, ... , l n = r (A) be the eigenvalues of A, repeated according to algebraic multiplicities. Then, via triangulization, fC(x) = P 1£ i£ n (x-(1+l i)n-1) = (x-(1+r (A)n-1)P 1£ i£ n-1 (x-(1+l i)n-1). Since the spectral radius r (C) = (1+r (A))n-1 is to be a simple eigenvalue of C, it follows that l i ¹ r (A), 1 £ i £ n-1. Hence r (A) is a simple eigenvalue of A. If x ³ 0 is an eigenvector of A, x is also an eigenvector of C and by Perron's theorem it is a multiple of x . Hence x is associated with the very eigenvalue r (A) of A. Finally, with A £ B ¹ A, C £ (I+B)n-1 ¹ C. By Perron's theorem (1+r (A))n-1 = r (C) < r ((I+B)n-1) = (1+r (B))n-1 , so that r (A) < r (B), completing the proof. #
Theorem. Let A ³ 0 be irreducible and B a complex matrix such that |B| £ A. Then r (B) £ r (A) and l = r (A)eif , (0 £ f < 2p ), is an eigenvalue of B iff there exists a unitary diagonal matrix D, such that B = eif DAD-1.
Proof: If (l , x) is an eigen-pair of B, using triangle inequality, |l ||x| = |Bx| £ |B||x| £ A|x|. By the corollary to Perron's theorem |l | £ r (A). Hence r (B) £ r (A). Next, if (l , x) is an eigenpair of B such that |l | = r (A), then r (A)|x| = |l ||x| £ |B||x| £ A|x|. By the last corollary, |x| > 0 and A|x| = r (A)|x| so that |l x| = |Bx| = |B||x| = A|x|. It follows that |B| = A and with f j denoting the argument of xj, if bkj ¹ 0, arg bkj + f j = arg l + f k(mod 2p ), (1 £ j, k £ n). Hence, if f = arg l , bkj = akj exp[i(f + f k - f j)], 1 £ j, k £ n, from which the result follows. #
Corollary 1. If A ³ 0 is irreducible, then (i) every eigenvalue of A of modulus r (A) is simple, (ii) if A has a total of k eigenvalues of magnitude r (A), these are r (A)e2p ij/k, 0 £ j < k and, moreover, for each eigenvalue l of A, l e2p ij/k, 0 < j < k, are also eigenvalues of A.
Proof: Applying the above theorem with B = A, if r (A)eif is an eigenvalue of A then A = eif Df ADf -1, say. From this, since r (A) is a simple eigenvalue of A, it follows that r (A)eif is also simple. Hence if eif r (A) and r (A)eiy are eigenvalues of A we have, say, A = ei(f ± y )(Df Dy ± 1)A(Df Dy ± 1)-1 = ei(f ± y )Df ± y ADf ± y -1. It follows that if l is an eigenvalue of A, l ei(f ± y ) is also an eigenvalue of A. Hence if the k eigenvalues of A of modulus r (A) are r (A)eif (j), 0 £ j < k, and 0 £ f (0) < f (1) < ... < f (k-1) < 2p , the set S = {eif (j) | 0 £ j £ k-1} under the usual multiplication, constitutes a subgroup of order k of the circle group G = {z | |z| = 1}. Since the only such subgroup is {1, w , w 2, ... , w k-1}, where w is the k-th root ei2p /k of unity, it follows that f (j) = 2p j/k, 0 £ j < k. The last assertion of the corollary is clear from this, completing the proof. #
Corollary 2. If A ³ 0 and B is a complex matrix such that |B| £ A, then r (B) £ r (A). In particular r (B) £ r (|B|).
Proof: If A is irreducible or 0 there is nothing to prove. If A is reducible we can find a permutation P such that PAPT is block upper-triangular with the square diagonal blocks irreducible. Since |B| £ A, PBPT has the same form as PAPT and the result follows from the previous theorem applied to the digonal blocks. #
PROBLEMS
1. Let A ³ 0 be irreducible with r (A) = 1. If A has a total of k eigenvalues of magnitude r (A), prove that the limit points of the sequence {Am}m³ 1 equal the distinct divisors of k in number. Deduce that {Am} is convergent iff k = 1.
2. Prove that a permutation matrix P such that pij = d s (i) j is irreducible iff s is a cyclic permutation. Also show that the multiplicity of the eigenvalue 1 of P equals the largest number of disjoint cycles the product of which equals the permutation s .
3. If A ³ 0 and Am is irreducible, where m ³ 2 is an integer, show that A is irreducible. Is the converse true?
4. Prove that A is irreducible iff |A|m is so for some m ³ 1.
5. Let ![]() and
and ![]() .
.
Find r (A), r (B), and directly verify that r (B) £ r (A). Does there exist a relation of type B = eif DAD-1? If so, find f and D.
6. Find an n´ n A of highest r (A) such that |aij| £ 1, 1 £ i, j £ n. Is A unique? What is r (A)?
The Structure of Cyclic Matrices
An irreducible A ³ 0 is called primitive if there is no eigen value of A of magnitude r (A), other than r (A) itself. If A ³ 0 is irreducible but is not primitive, it is called imprimitive, or, cyclic. If A is cyclic and has k > 1 eigenvalues of magnitude r (A), it is called cyclic of index k. This k is also known as the index of imprimitivity of A.
The structure of cyclic matrices is described in the following:
Theorem. Let A ³ 0. Then: (i) A is primitive iff Am > 0, for some m ³ 1, and (ii) A is cyclic of index k > 1 iff there exists a permutation Q such that in a block partitioned form
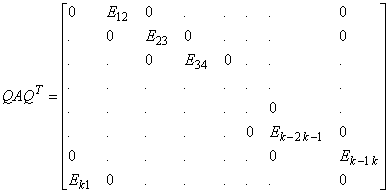
where the diagonal blocks are square and each of the k cyclic products B1 = E12E23E34 ... Ek-1 kEk1, B2 = E23E34 ... Ek-1 k Ek1E12, … , Bk = Ek1E12E23 ... Ek-1 k is primitive.
Consequently, if the first diagonal block 0 is p
´ p, the characteristic polynomial of A is given byfA(x) = xn-kp|xkI-B| = xn-kp
P 1£ j£ p (xk-m j) = xn-kpfB(xk),where
m j's are the p eigenvalues of B º B1 . The matrix A has at least n-kp zero eigenvalues, precisely k simple eigenvalues of magnitude r (A), namely, r (A), w r (A), w 2r (A), ... , w k-1r (A), where w = exp[2p i/k]), and a rotation of the complex plane by integral multiples of the angle 2p /k maps the entire set of eigenvalues of A (repeated according to algebraic multiplicities) onto itself.Proof: If, say, Am > 0 and k is any positive integer, Amk > 0 so that by Perron's theorem (
r (A))mk is a simple eigenvalue of Amk and that there is no other eigenvalue of this magnitude. Since the eigenvalues of Amk are precisely {l 1mk, l 2mk, ... , l nmk}, where the eigenvalues of A are {l 1, l 2, ... , l n} repeated according to their algebraic multiplicities), if A is not primitive we are immediately led to a contradiction by the Corollary 1 above.Conversely, let A be primitive. Using the irreducibility of A for each 1
£ j £ n, there is a path in G(A) of length lj, say, connecting Gj with itself. Here, as stated before, the length of a loop is taken to be 1. Then, using the non-negativity of A, the j-th diagonal element in the lj-th power of A is positive. It follows that Al , where l = P 1£ j£ n lj, has all positive diagonal elements. It is next to be shown that Al is irreducible. If not, there is a permutation matrix P such that in the block-partitioned formPAlPT = ![]() .
.
If
x , z > 0 are respectively the eigenvectors of A and AT corresponding to the eigenvalue r(A), writingPx = [x y]¢ , and Pz = [z t]¢ , one has My = (r (A))ly and KTz = (r (A))lz. It follows that (r (A))l is an eigenvalue of both M and K so that it is at least a double eigenvalue of Al, contradicting the primitivity of A. Thus Al must be irreducible. Due to the positivity of its diagonal elements we can write Al = m I + C, where m > 0 and G(C) is strongly connected, so that C is irreducible. It follows that Al(n-1) > 0, proving that some (positive integral) power of A is positive.Next let A be cyclic of index k. Then
r (A)exp(2p i/k) is an eigenvalue of A and using |A| £ A there exists a unitary diagonal matrix D such that A = exp(2p i/k) DAD-1. Let the distinct diagonal entries in D be exp(id j), 1 £ j £ s. Then s ³ 2 and since a scalar multiplication of D does not affect the expression DAD-1, we can assume that 0 = d 1 < d 2 < ... < d s < 2p . Let Q denote a permutation matrix that regroups the diagonal elements in D so that D = QDQT = diag [exp(id 1)I1, exp(id 2)I2, ... , exp(id s)Is] where Ij is an identity matrix of size sj´ sj, 1 £ j £ s. LetE = QAQT = 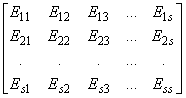 ,
,
where the (p, q)-th block Epq is of size sp
´ sq , so that comparing the (p, q)-th blocks in E = exp(2p i/k) D E(D )-1, we have Epq = exp(i{(2p /k) + d p - d q})Epq, (1 £ p, q £ s). Since E is irreducible as A is, no row-block in E can be entirely zero and since |d r - d q| < 2p , (1 £ r, q £ s), it follows that for each p there is precisely one q such that (2p /k) + d p - d q = 0 (mod 2p), and Epq ¹ 0. Putting q = s (p), from the irreducibility of A, it follows that s must be a cyclic permutation on the set {1, 2, ... , s} and hence that the separation between any two dp's is a multiple of 2p /k. Moreover, summing over all 1 £ p £ s, (2p s/k) + S d p - S d s (p) = 2p s/k = 0 (mod 2p ), which shows that s is a multiple of k. Now, from 2p = (2p +d 1 - d s) + (d s - d s-1) + ... + (d 2 - d 1) ³ (2p /k)s, it follows that s = k, d p+1 = (2p /k) + d p, 1 £ p < s, and hence that d p = 2p (p-1)/k and s (p) = p+1, 1 £ p < s, and s (s) = 1. Thus QAQT has the desired canonical form. The required form of the characteristic polynomial of A is obtained by evaluating the determinant below by adding x-1Ej-1, j times the j-th row-block to the (j-1)-th, j = k, k-1, ... , 2, so as to get a block lower triangular matrix: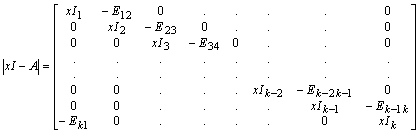
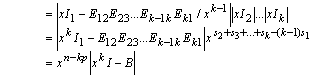
which also implies that A has at least n-kp zero eigenvalues, just k simple eigenvalues
r (A), w r (A), w 2r (A), … , w k-1 r (A) of magnitude r (A), and that a rotation of the complex plane by integral multiples of the angle 2p /k maps the entire set of eigenvalues of A, repeated according to their algebraic multiplicities, onto itself.Note that (QAQT)k = diag (E12 ...Ek1 , E23 ...E12 , ... , Ek1 ...Ek-1 k) = diag (B1, B2, ... , Bk). Since B1 = B has (
r (A))k as a simple eigenvalue and since the factors in B1, B2, ... , Bk are the same, but cyclically permuted, each of B1, B2, ... , Bk have the same non-zero eigenvalues upto their algebraic multiplicities and hence each Bj has ((r (A))k = r (Bj) as a simple eigenvalue. Moreover, each Bj is non-negative. To establish their primitiveness it remains to show that each Bj is irreducible.Using the Perron-Frobenius theorem, as A is irreducible, let
x denote a positive eigenvector of A associated with its eigenvalue r (A). If some Bj is not irreducible, let P be a permutation matrix such thatPBjPT = ![]() .
.
Let Q
x = (x 1T, x 2T, ... , x kT) , where x i is si´ 1. Further put Px = [xT | yT]T, where if F is s´ s then x is s´ 1. It follows that![]() .
.
Since y > 0, it is an eigenvector of H associated with the eigenvalue (r (A))k .
Similarly, let h > 0 be an eigenvector of AT associtaed with the eigenvalue r (A) and put Qh = (h 1T, h 2T, ... , h kT)T and Ph = [uT | vT]T, so that
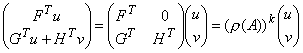 ,
,
implying that u is an eigenvalue of FT associated with its eigenvector (r (A))k . It follows that Bj has (r (A))k at least as a double eigenvalue. This contradicts the already proven simplicity of the eigenvalue (r (A))k of Bj. Thus each Bj must be irreducible.Conversely, if A has such a structure with each of the Bj primitive: via (QAQT)k , in the graph of QAQT each node of each row block is connected with all the rest and hence in it at least one node of each row block must be connected with with at least one node of the cyclically next row block. It follows that G(QAQT) is connected and so A is irreducible, which, as fA(x) = |xkI-B|xn-pk and B is primitive, implies that A is k-cyclic. #
PROBLEMS
1
. Find all 1´ 1, 2´ 2, 3´ 3 and 4´ 4 matrices with entries 0 and 1 only which are: (a) reducible, (b) irreducible, (c) primitive, (d) cyclic of index k, where k = 1, 2, 3, 4, and, 5.2. Find a permutation P such that PAP' for the following matrix A is block upper triangular with the square diagonal blocks irreducible. Also determine which of the diagonal blocks are primitve and compute the index of imprimitivity of the rest.
 .
.
3. If A ³ 0 is irreducible and aii ¹ 0 for some i, show that Am > 0 for some m.
4. Prove that A ³ 0 is primitive iff all but a finite number of positive integral powers of A are positive.
5. If A ³ 0 and Aj is primitive, what can you say about Am?
6. If A ³ 0 and Aj is k-cyclic, what can you say about Am?