Chapter 12

STABILITY OF A MATRIX

An matrix A Î C ⁿ´ n is called stable if the initial value problem (IVP): dx/dt = Ax, x(0) = x₀, has a solution x(t) ® 0, as t ® ¥ , for any choice of the initial vector x₀, whatsoever. Note that the solution of the IVP is given by x(t) = e^tA x₀, where e^At º e^tA = I+tA+(t²/2!)A²+...+(tⁿ/n!)Aⁿ+... . Hence, a necessary and sufficient condition for the stability is e^At ® 0, as t ® ¥ . This is equivalent to r (e^A) < 1, where r (B) denotes the spectral radius of the matrix B and is the largest magnitude of the eigenvalues of B. The condition is equivalent to e^{Rl (}l ) < 1 Û Rl (l ) < 0, for each eigenvalue l = l (A) of A. Hence A is stable iff all the eigenvalues of A lie in the open left half plane {z : Rl z < 0} or using the notion of inertia that In (A) = (0,n,0).

PROBLEMS

.

2. Show that A is stable iff A* is stable iff A¢ is stable.

5. Prove that an n´ n complex matrix A is stable if it satisfies Rl a_ii > S _j¹ i |a_ij | > 0, 1 £ i £ n.

6. Prove that a real 2´ 2 symmetric matrix

8. If In A = (p ,n ,d ), show that for the matrix

In B = (p ,n ,p +n +2d ). Deduce that B-cI is stable for all complex c with Re c > 0 iff A is stable.

Lyapunov’s Stability Theorem

As such the notion of stability of a matrix involves a knowledge of the eigenvalues of the matrix. We know that a determination of the eigenvalues of a general matrix is a transcendental process in the sense that it involves an infinity of arithmetic operations. Thus, first determining the eigenvalues (even if by an approximate numerical method, and then checking if their real parts are all negative is not the right way of establishing the stability of a matrix. In this context, the celebrated Lyapunov’s stability theorem enables a theoretical determination of the stability of a matrix by using only a finite number of arithmetic operations in solving a linear system and then determining if a certain matrix is positive definite or not.

Lyapunov’s Stability Theorem. If A is stable and C is a positive definite matrix there exists an X p.d. such that AX+XA^* = -C. Conversely, if X, C are p.d. and the above equation is satisfied, then A is stable.

Proof: If the equation is satisfied with X, C p.d. let (l , y) be an e.p. (eigen pair) of A^*, i.e., y ¹ 0 and Ay = l y. Pre-and post-multiplying the equation by y^* and y, respectively, we have –y^*Cy = (A^*y)^*Xy+y^*XA^*y = (l ^*+l )y^*Xy. Since y^*Cy, y^*Xy > 0 Þ l ^*+l < 0, i.e., Rl l < 0, showing that A is stable.

Conversely, let A be stable. Then s (A)Ç s (-A^*) = f and so the system AX+XA^* = -C has a unique solution X for every C. If C is positive definite, *-ing the equation (i.e., taking the adjoint or the conjugate transpose on both sides) we have -C = X^*A^*+AX^* = AX^*+X^*A . It follows from the uniqueness of the solution that X = X^*, i.e., X is hermitian.

Since A is stable so is A^* and so both e^At and e^{A* t} ® 0, as t ® ¥ . Hence e^AtC e^{A* t} ® 0, t ® ¥ . But (d/dt)( e^AtC e^{A* t}) = Ae^AtC e^A*t+e^AtC e^{A* t} A^*, i.e., (d/dt)Z(t) = AZ(t)+Z(t)A^*, where Z(t) = e^AtCe^A*t.Integrating w.r.t. t from 0 to ¥ , we therefore have

-C = Z(¥ ) – Z(0) = = AX+XA^*, X = .

Note that the existence of the integral is guaranteed by the fact that A is stable. If s = max{Rl l : l an e.v. of A} < 0, r (e^A ) = es . Consequently, there is a matrix norm ||.||₁ s.t. ||e^A||₁ < es ^+d < 1, for a d sufficiently small so that s +d < 0. Similarly, ||e^A*||₂ < es ^+d < 1. Hence ||e^AtC e^{A* t}|| £ ||e^At|| ||C|| ||e^{A* t}|| £ C₁ ||e^At ||₁ ||C||C₂||e^{A* t}||₂. But for any matrix norm ||× ||, ||e^Bt || £ ||e^B[t]|| ||e^B(t-[t]) || £ ||e^B||^[t] e^||B||(t-[t]) £ ||e^B||^t e^||B||/ ||e^B||, if ||e^B|| < 1. Put e^-a = max {||e^A||₁, ||e^A*||₂} < 1, i.e., a > 0. Then ||e^AtC e^A*t|| £ C₁C₂CQe^{-2a t}, where

Choosing the matrix norm ||× || to be ||X|| = n´ max{|X_ij| : 1 £ i, j £ n}, the integral converges by the Lebesgue’s dominated convergence theorem.

Finally, to show that X is p.d., let z ¹ 0. Then z^*Xz = > 0, the integrand being positive for all t > 0, as C is positive definite. Hence, z^*Xz > 0 Þ X is p.d., completing the proof of the Lyapunov’s stability theorem. #

PROBLEMS

1. Is it true that AX+XA^* is necessarily negative define if A is stable and X is positive definite? If so give a proof? If not, produce a counter example.

2. The left hand side of AX+XA^* = -C, is a linear vector function in the n²-variables x_ij‘s. Produce a matrix B and a vectror c such that Bx = c, where x = vec (X) is defined by x_i+(j-1)n = (X)_ij for all 1 £ i, j £ n.

3. Check the stability of the following matrices:

.

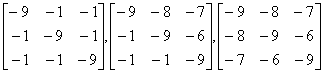4. Let the hermitian part H of a complex matrix A be defined by H = (A+A^*)/2 and the skew hermitian part S by S = (A-A^*)/2. If the hermitian part H of A is negative definite prove that A is stable. Is the converse also true?

Equivalent Formulations of Sylvester’s Inertia Theorem

Recall that the inertia of a matrix A is defined as the triple In(A) = (p (A), n (A), d (A)), where the entries respectively denote the number of eigenvalues with positive, negative and zero real parts. Thus an n´ n matrix A being stable is equivalent to In(A) = (0, n, 0). The following equivalents of Sylvester’s inertia theorem are sometimes useful in determining stability of certain matrices:

Theorem. Let H_n denote the class of all n´ n hermitian matrices and B > 0 mean that B is p.d. The following statements are equivalent: (a) If H Î H_n and S is non-singular, In(S^*HS) = In(H) (Sylvester’s law of inertia). (b) If P > 0 and H Î H_n, In(PH) = In(H). (c) If AH > 0 and H Î H_n Þ In A = In H.

Proof: Note that In (S^*HS) = In (S^-1((SS^*)H)S) = In ((SS^*)H) and that In ((AH)^-1H) = In (H^-1A^-1H) = In (A^-1) = In A. Hence, taking P = SS^*, (a) Ü (b). Taking S to be such that SS* = P (e.g., LL*-decomposition, or S = Ö P), (b) Ü (a). Hence (a) Û (b). Taking P = (AH)^-1, (b) Þ (c). Finally, assume (c). If H is non-singular, choosing A = P^-1H^-1, so that P = (AH)^-1, In (PH) = In (HP) = In (HP)^-1 = In A = In H. Thus (c) Þ (b) for H non-singular, which by the above proof of (b) Þ (a) shows that (a) holds for non-singular H. Hence (c) Þ (a) in the non-singular case and to complete the proof it is sufficient to show that (a) in the non-singular case implies (a) in the singular case. This we do below:

If H is singular, let H(d ) denote the matrix obtained from the unitary diagonalization of H by replacing the zero diagonal entries by d . Let d > 0 and sufficiently small. Then H(d ) and S^*H(d )S have the same number of negative eigen values as H. Passing to the limit as d ® 0, we find that H and S^*HS have the same number of negative eigen values (since a positive eigen value could at best tend to zero). Replacing H by -H it follows that they have the same number of positive eigen values and therefore also the same naumber of zero eigen values. This completes the proof. #

PROBLEMS

1. Prove that for a complex matrix A there holds A = PH, where P is positive definite and H is hermitian iff p_A(x) = P _{1£ j£ k} (x-c_j), where c_j‘s are real and distinct.

2. Is it true that a hermitian H is stable iff -H is p.d.? [Give two reasonings, one of which uses Lyapunov’s theorem].

3. If H is hermitian an non-singular, H(-H)+(-H)H = -2H² and 2H² is positive definite. What do you conclude?

Some Equivlaent Criteria of Stability

Theorem. For an n´ n complex matrix A, the following statements are equivalent:

(1) A is stable (i.e., s (A) Ì {z: Rl z < 0}.

(2) All solutions of the system dx/dt = Ax approach zero as t ® ¥ .

(3) lim_t® ¥ e^At = 0.

(4) For a > 0, A-a I is non-singular and the spectral radius of B = (A-a I)^-1(A+a I) is less than unity.

(5) For a > 0, A-a I is non-singular and H = (A-a I)^-1(A+a I) is convergent (i.e., H^k ® 0 as k ® ¥ .

(6) For a > 0, A-a I is non-singular and the sequence {x_k} defined by (A-a I)x_k+1 = -(A+a I)x_k+2b, converges to the solution of the linear system Ax = b, for any initial guess x₀.

(9) There exists H p.d. such that Rl (x^*AHx) < 0, for all non-zero x Î C ⁿ.

(13) For C n.d., the matrix equation A^*H+HA = C has a solution and 0 ¹ AY+YA^* p.s.d. implies tr (Y) < 0.

(14) For a > 0, A-a I is non-singular and for every negative definite C there exists H p.d. such that BHB^*-H = C, where B = (A-a I)^-1(A+a I).

(15) For a > 0, A-a I is non-singular and there exists H p.d. such that BHB^*-H is n.d., where B = (A-a I)^-1 (A+a I).

Proof: The implications (1) Û (3) Û (2) have already been proved above. Next, A-a I is non-singular and |l ((A-a I)^-1 (A+a I))|² = |(l (A)+a )/(l (A)-a )|² = {(Rl l (A)+a )²+(Im l (A))²}/{(Rl l (A)-a )²+(Im l (A))²} < 1, iff Rl l (A) < 0. Hence (1) Û (4) Û (5) Û (6).(1) Þ (7) has been proved before and clearly (7) Þ (8). Also (8) Þ (1) is proved before. Thus (1) Þ (7) Þ (8) Þ (1).

With H as in (8), if x Î C ⁿ is non-zero then 0 > x^*(AH+HA^*)x = 2 Rl (x^*AHx). Hence (8) Þ (9). Converlely, if there is H p.d. such that Rl (x^*AHx) < 0 for x Î C ⁿ not zero, it follows that AH+HA is n.d. Hence (9) Þ (8). Consequently (9) Û (8).

Noting that W(AH) = {x^*AHx : x^*x = 1}, W(AH) Ì {z : Rl z < 0} Û Rl x^*AHx < 0, x ¹ 0. Hence (9) Û (10).

To prove that (11) Þ (1), we have to show that (via similarity) that the sum of a skew-hermitian K and a negative definite Q is stable. For this, if x ¹ 0, (x^*Kx)^* = x^*K^*x = - x^*Kx Þ Rl x^*Kx = 0. Hence, as I is p.d., for every x ¹ 0, Rl (x^*(K+Q)Ix) = Rl (x^*Qx) = x^*Qx < 0. By (9) Þ (1), K+Q is stable. Thus (11) Þ (1).

Conversely, if (1) holds and E_m = (1/m)J_m , m = 1, 2, ... , where J_m is the Jordan canonical form of mA, E_m is simialr to A. If m is suficiently large, -(1/2)(E_m+E_m^*) = Q is a tridiagonal matrix which is real, symmetric, strictly diagonally dominant with positive diagonal entries (negatives of real parts of e.v.’s of A) and hence is p.d. (|-l (Q)+Rl l (A)| < 2/m Þ -Rl l (A) -2/m £ -l (Q) £ -Rl l (A)+2/m Þ l (Q) > 0 : Gershgorin circle theorem). Hence E_m = (E_m+E_m^* )/2+(E_m-E_m^*)/2 = Q+K, where Q is n.d. and K is skew-hermitian. Hence by the similarity of A and E we have (1) Þ (11).

Thus (1) Û (11).

Assuming (12), i.e., A = (S+Q₁) H, H p.d., Q₁ n.d. and S skew-hermitian, we have A = (Ö H)^-1(Ö H(S+Q₁)Ö H)Ö H = (Ö H)^-1(K+Q)Ö H, where K is skew-hermitian and Q is n.d. Thus (12) Þ (11).

Conversely, if A = C^-1(K+Q)C, K skew hermitian, Q n.d., we have A = C^-1(K+Q)(C^-1)^*(C^*C) = (S+Q₁)H, where S = C^-1K(C^-1)^* skew-hermitian, Q₁ = C^-1Q(C^-1)^* n.d. and H = C^*C p.d. Hence (11) Þ (12) and so (11) Û (12).

To prove (1) Þ (13), by (1) Þ (7), for n.d. C, A^* being stable as A is, A^*H+HA = C has a p.d. solution H. Also, if 0 ¹ AY+YA^* = G is p.s.d., since Y is unique (s (A)Ç s (-A ) = f ), for each xÎ C ⁿ,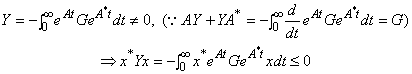

Consequently Y is n.s.d. and as Y ¹ 0, tr Y < 0. Hence (1) Þ (13).

Conversely, let (13) hold. Let (l , y) be an e.p. of A. Let Y₁ = (y | y | ... | y). Then with Y = Y₁Y₁^*, if Rl l > 0, AY+YA^* = A Y₁Y₁^*+Y₁(AY₁)^* = (l +l ^*)Y₁Y₁^* ¹ 0 is p.s.d. but tr Y = tr (Y₁Y₁^*) > 0, #, a contradiction. Hence Rl l < 0. Then, since for n.d. C, A^*H+HA = C has a solution H and as also A^*H^*+H^*A = C, w.l.g., H can be assumed to be hermitian (else take (H+H^*)/2 as solution). Then 0 > y^*Cy = y^*A^*Hy+y^*HAy = (l ^*+l )y^*Hy Þ l ^*+l = 2 Rl l ¹ 0. Hence Rl l < 0 for every e.v. l of A. Consequently A is stable. Thus (13) Þ (1). Hence (1) Û (13).

Next, assume (4). Then r (B) < 1. Let C = -E be n.d. If X-BXB^* = 0, we have X = B^mX(B^m)^* ® 0, m ® ¥ . Hence X = 0, and so the homogeneous system X-BXB = 0, has only trivial solution. Consequently, the system H - BHB = E has a solution H (unique all the more) for every E and so for the present p.d. E. Define H_m = E + BH_m-1B , m = 1, 2, ... . Then, for an arbitrary H₀ , since r (B) < 1, H_m-H = B(H_m-1 -H)B* = B^m(H₀ - H)(B^*) ® 0, m ® ¥ . Hence H = lim_m® ¥ H_m. With H₀ = I, H_m = E + BEB^* + ... + B^m-1 E(B^m-1)^*+B^m(B^m)^* and so x^*H_mx ³ x^*Ex > 0, for all x ¹ 0. Taking limit as m ® ¥ , x^*Hx ³ x^*Ex > 0, for all x ¹ 0. Hence H is p.d. Thus (4) Þ (14). Taking H as in (14) we have (14) Þ (15).

If (15) holds, H is p.d. and H –BHB^* is also p.d. Let (l , u) be an e.p. of B^*. Then 0 < u^*Hu –u^*BHB^*u = (1 -|l |²)u^*Hu. Hence 1 -|l |² > 0, i.e., |l | < 1. Hence r (B) = r (B^*) < 1. Thus (15) Þ (4). Hence (4) Þ (14) Þ (15) Þ (4).

Summarizing, we have proved the implications:

 from which the equivalence of (1)-(16) follows. #