A crystal is an array of atoms packed together in a regular pattern. A unit cell of a pattern is a piece of the pattern which, when repeated through space without rotation and without gaps or overlaps, reconstructs the pattern to infinity. For filling space without holes, a unit cell must be either a parallelogram (in 2D) or a parallelepiped (in 3D).
The symmetries of a pattern determine the shape of the unit cell. For example, mirror symmetry requires a rectangular (in 2D) or tetragonal (in 3D) unit cell. There is an infinite number of possible unit cells for any pattern (e. g., a given unit cell can generate a family of unit cells by repeated doublings in size). By custom, the unit cell is chosen to be the smallest one that reveals the special geometry characteristic of the symmetry. Thus, although an oblique parallelogram can be used for a pattern with 4-fold symmetry in 2D, a square is preferred.
When a unit cell is repeatedly translated to fill all of 2D or 3D space, the vertices of all the unit cells in the filled space constitute a lattice. A lattice is an infinite array of regularly-spaced points. All points in the lattice have identical "environments" --- the view from every point in the lattice is identical to that from any other point in the lattice. The absolute positions of the points of a lattice, and hence the unit cell, are arbitrary with respect to a pattern.
Not all lattice points need coincide with unit cell vertices. Primitive unit cells use every lattice point as a unit cell vertex. Non-primitive unit cells, however, contain extra lattice points not at the corners.
A primitive unit cell contains exactly one lattice point. For example in 2D, each primitive unit cell joins four lattice points, each of which counts for 1/4 because every lattice point is shared among four unit cells. In 2D, a non-primitive unit cell has one additional lattice point exactly centered within it and is called a body-centered non-primitive unit cell. In 3D, non-primitive cells are of three kinds:
Although primitive unit cells are simpler than non-primitive unit cells, the non-primitive unit cell is preferred when its geometry is more favorable (simpler). For instance, a rectangular non-primitive cell would be chosen over a rhomboid primitive cell. In general, the unit cell used is the smallest one with the most regular geometry.
A lattice may be specified by two non-coincident vectors in 2D, and by three non-coplanar vectors in 3D. The vectors lie along the edges of the unit cell, and are labeled a, b, and (in 3D) c. The magnitude of the vectors is given by the dimensions of the unit cell in the real crystal under study.
The faces of the unit cell are labeled as follows:
Similarly, the inter-facial angles of the unit cell are defined to be:
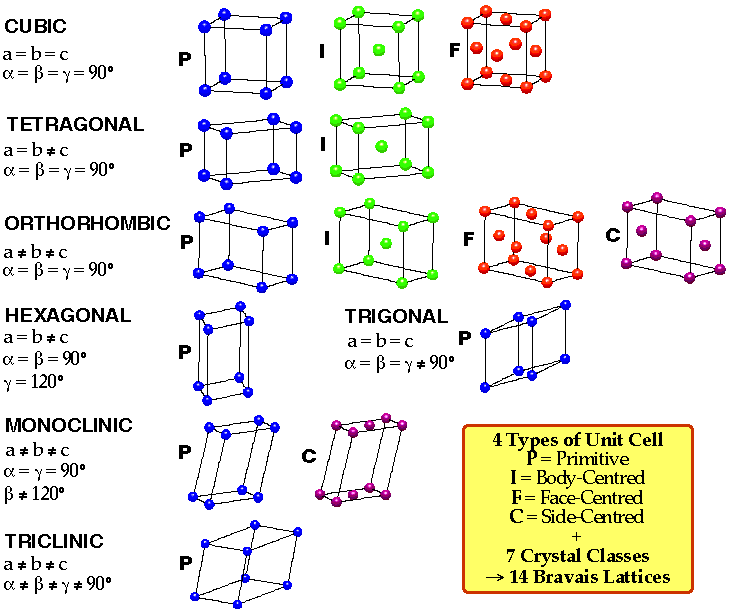
Lattices can be classified into "systems", each system being characterized by the shape of its associated unit cell. In three dimensions, the lattices are categorized into seven crystal lattice "systems". Within several of these, lattices supporting non-primitive unit cells can be defined. The classification scheme yields a total of 14 possible lattices (called Bravais lattices).
The lattice symbols used for classification are as follows:
| System | # of lattices in system | Lattice symbols |
|---|---|---|
In two dimensions, there are only four possible unit cell shapes and two possible lattice symbols:
| Cell shape | Lattice symbol |
|---|---|
| General parallelogram (rhomboid) | p |
| Rectangle | p, c |
| Square | p |
| Rhombus with 60 degree angle | p |
