LECTURE 14

Enthalpy of a compressed liquid

Determine the enthalpy of water at 100^o C and 15 MPa (a) by using compressed liquid tables, (b) by approximating it as a saturated liquid, and (c) by using the correction factor.

At 100^oC, the saturation pressure of water is 101.35 kPa, and since P>P_sat, the water exists as a compressed liquid at the specified state.

(a) from the compressed liquid tables,

P = 15 Mpa, T = 100^oC, h = 430.28 kJ/kg

This is the exact value.

(b) Approximating the compresses liquid as a saturated liquid at 100^oC, as is commonly done, we obtain

h = h_{f@100 C} = 419.04 kJ/kg

This value is in error by about 2.6 percent.

(c) From equation

h_{@ P,T} = h_f@T + v_f@T (P – P_sat)

= 419.04 + 0.001(15000 – 101.35) kJ/kg

= 434.60 kJ/kg

Problem # 1 (Nozzle)

Nitrogen gas flows into a convergent nozzle at 200 kPa, 400 K and very low velocity. It flows out of the nozzle at 100 kPa, 330 K. If the nozzle is insulated, find the exit velocity.

V_i = 0

Adiabatic nozzle

The SSSF equation:

V_e²/2 = (h_i – h_e) = C_p(T_i – T_e)

= {gR_u/M(g-1)} (T_i – T_e)

= {1.4 * 8314/(28*0.4)}(400-330)

= 72747.5 m²/s²

We get, V_e = 381.44 m/s

Problem # 2 (Diffuser)

Air at 10^o C and 80 kPa enters the diffuser of a jet engine steadily with a velocity of 200 m/s. The inlet area of the diffuser is 0.4 m². The air leaves the diffuser with a velocity that is very small compared with the inlet velocity. Determine (a) the mass flow rate of the air and (b) the temperature of the air leaving the diffuser.

Solution:

Assumptions: This is a steady flow process. Air is an ideal gas. The potential energy change is zero. Kinetic energy at diffuser exit is negligible. There are no work interactions. Heat transfer is negligible.

To determine the mass flow rate, we need the specific volume of air.

v₁ = RT₁/ P₁ = 0.287 * 283 / 80 = 1.015 m³/kg

m = 1/v₁(V₁A₁) = (200 * 0.4)/ 1.015 = 78.8 kg/s

For steady flow, mass flow through the diffuser is constant.

(b) (h₁ + V₁²/2) = (h₂ + V₂²/2) (since Q = 0, W = 0, and DPE = 0)

h₂ = h₁ – (V₂²- V₁²)/2

The exit velocity of a diffuser is very small and therefore neglected.

h₂ = h₁ + V₁²/2

T₂ = T₁ + V₁²/2C_p

T₂ = 283 + 200²/(2*1004)

= 302.92 K

Compressing air by a compressor

Air at 100 kPa and 280 K is compressed steadily to 600 kPa and 400 K. The mass flow rate of air is 0.02 kg/s and a heat loss of 16 kJ/kg occurs during the process. Assuming the changes in KE and PE are negligible, determine the necessary power input to the compressor.

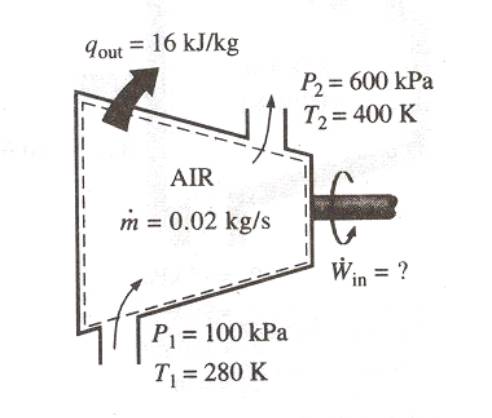
We take the compressor as the system. This is a control volume since the mass crosses the system boundary during the process. Heat is lost from the system and work is supplied to the system.

With similar assumptions as in the diffuser problem,

w = q + (h₂ – h₁)

The input power = m (q + (h₂ – h₁))

= 0.02 (16 + (1.004*(400 – 280)))

= 2.73 kW

Power generation by a steam turbine

The power output of an adiabatic steam turbine is 5 MW, and the inlet and exit conditions of the steam are as indicated in the figure.

(a) Compare the magnitude of Dh, DKE, and DPE

(b) Determine the work done per unit mass of the steam flowing through the turbine

(c) Calculate the mass flow rate of the steam.

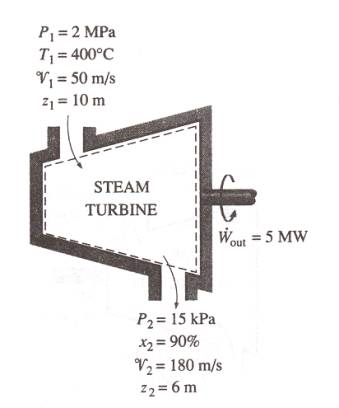
We take the turbine as a system. The control volume is shown in the figure. The system, the inlet and exit velocities do work and elevations are given and thus the kinetic and potential energies are to be considered.

At the inlet, the steam is in superheated vapor state.

h₁ = 3247.6 kJ/kg.

At the turbine exit, we have a saturated liquid-vapor mixture at 15 kPa pressure. The enthalpy at this state is

h₂ = h_f + x₂h_fg

= 225.94 + 0.9 * 2373.1

= 2361.73 kJ/kg

Dh = h₂ – h₁

= 2361.73 – 3247.6 = -885.87 kJ/kg

Dke = (V₂²- V₁²)/2 = (180²-50²)/2*1000

= 14.95 kJ/kg

DPe = g(Z₂-Z₁) = 9.807 * (6 –10)/1000

= -0.04 kJ/kg

w_out = -[( h₂ – h₁) +(V₂²- V₁²)/2 + g(Z₂-Z₁)]

= -[-885.87 + 14.95 – 0.04]

= 870.96 kJ/kg

(d) The required mass flow rate for a 5MW power output is 5000/870.96 = 5.74 kg/s