Thermodynamic Temperature Scale
To define a temperature scale that does not depend on the thermometric property of a substance, Carnot principle can be used since the Carnot engine efficiency does not depend on the working fluid. It depends on the temperatures of the reservoirs between which it operates.

Consider the operation of three reversible engines 1, 2 and 3. The engine 1 absorbs energy Q1 as heat from the reservoir at T1, does work W1 and rejects energy Q2 as heat to the reservoir at T2.
Let the engine 2 absorb energy Q2 as heat from the reservoir at T2 and does work W2 and rejects energy Q3 as heat to the reservoir at T3.
The third reversible engine 3, absorbs energy Q1as heat from the reservoir at T1, does work W3 and rejects energy Q3 as heat to the reservoir at T3.
h1 = W1 / Q1 = 1- Q2/Q1 = f(T1,T2)
or, Q1/Q2 = F(T1,T2)
h2 = 1- Q3/Q2 = f(T2,T3)
or, T2/T3 = F(T2,T3)
h3 = 1- Q3/Q1 = f(T1,T3)
T1/T3 = F(T1,T3)
Then , Q1/Q2 = (Q1/Q3)/(Q2/Q3)
Or, F(T1,T2) = F(T1,T3) /F(T2,T3)
Since T3 does not appear on the left side, on the RHS also T3 should cancel out. This is possible if the function F can be written as
F(T1, T2) = f(T1) y (T2)
f(T1) y (T2) = {f(T1) y (T3)} / {f(T2) y (T3)}
= f(T1) y (T2)
Therefore, y (T2) = 1 / f(T2)
Hence, Q1 / Q2 = F(T1,T2) = f(T1)/ f(T2)
Now, there are several functional relations that will satisfy this equation. For the thermodynamic scale of temperature, Kelvin selected the relation
Q1/Q2 = T1/T2
That is, the ratio of energy absorbed to the energy rejected as heat by a reversible engine is equal to the ratio of the temperatures of the source and the sink.
The equation can be used to determine the temperature of any reservoir by operating a reversible engine between that reservoir and another easily reproducible reservoir and by measuring efficiency (heat interactions). The temperature of easily reproducible thermal reservoir can be arbitrarily assigned a numerical value (the reproducible reservoir can be at triple point of water and the temperature value assigned 273.16 K).
The efficiency of a Carnot engine operating between two thermal reservoirs the temperatures of which are measured on the thermodynamic temperature scale, is given by
h1 = 1- Q2/Q1 = 1 – T2/T1
The efficiency of a Carnot engine, using an ideal gas as the working medium and the temperature measured on the ideal gas temperature scale is also given by a similar expression.
(COP)R = QL /(QH – QL) = TL / (TH – TL)
(COP)HP= QH /(QH – QL) = TH / (TH – TL)
Clausius Inequality
For a Carnot cycle
Q1/Q2=T1/T2
Or Q1/T1-Q2/T2=0 for a reversible engine.
With the usual sign convention, that is, heat flow into a system taken as positive and heat outflow of the system taken as negative
Q1/T1+Q2/T2=0 or SQi/Ti=0
For an irreversible engine absorbing Q1 amount of heat from a reservoir at T1 and rejecting Q21 to a reservoir at T2, then
1-Q21/Q1<1-Q2/Q1
or 1-Q21/Q1<1-T2/T1
or Q21/Q1>T2/T1
or Q21/T2>Q1/T1
making use of the sign convention, we get
Q21/T2+Q1/T1<0
Or SQ/T<0 for an irreversible engine
Replacement of a Reversible process by an equivalent process
Let us consider cyclic changes in a system other than heat engines. If the cycle can be split up into a large number of heat engine cycles then the above observation can be made use of in relating the heat interactions with the absolute temperatures.
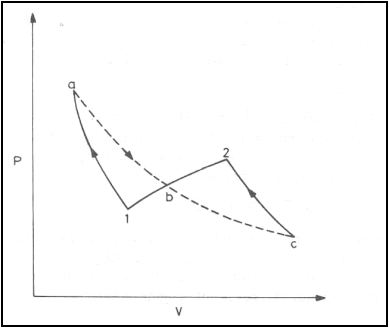
Any reversible process can be approximated by a series of reversible, isothermal and reversible, adiabatic processes.
Consider a reversible process 1-2. The same change of a state can be achieved by process 1-a (reversible adiabatic process), isothermal process a-b-c and a reversible adiabatic process c-2. The areas 1-a-b and b-c-2 are equal. From the first law
U2-U1=Q1-a-b-c-2-W1-a-b-c-2
Consider the cycle 1-a-b-c-2-b-1. The net work of the cycle is zero. Then
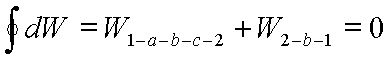
or
![]()
the heat interaction along the path 1-a-b-c-2 is
Q1-a-b-c-2=Q1-a+Qa-b-c+Qc-2=Qa-b-c
Since 1-a and c-2 are reversible adiabatic paths. Hence
U2-U1=Qa-b-c-W1-b-2
Application of the first law of the thermodynamics to the process 1-b-2 gives
U2-U1=Q1-b-2-W1-b-2
Comparing the two equations
Qa-b-c=Q1-b-2
The heat interaction along the reversible path 1-b-2 is equal to that along the isothermal path a-b-c. Therefore a reversible process can be replaced by a series of reversible adiabatic and reversible isothermal processes.
Clausius Inequality
A given cycle may be subdivided by drawing a family of reversible, adiabatic lines. Every two adjacent adiabatic lines may be joined by two reversible isotherms.
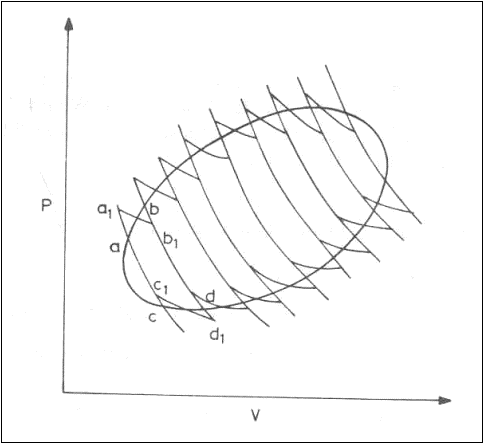
The heat interaction along the reversible path is equal to the heat interaction along the reversible isothermal path.
The work interaction along the reversible path is equal to the work interaction along the reversible adiabatic and the reversible isothermal path.
That is,
Qa-b=Qa1-b1 and Qc-d=Qc1-d1
a1-b1-d1-c1 is a Carnot cycle.
The original reversible cycle thus is a split into a family of Carnot cycles. For every Carnot cycle
![]() . Therefore for the
given reversible cycle,
. Therefore for the
given reversible cycle,
![]()
If the original cycle is irreversible
![]()
so the generalized observation is
![]()
Whenever a system undergoes a cyclic change, however complex the cycle may be( as long as it involves heat and work interactions), the algebraic sum of all the heat interactions divided by the absolute temperature at which heat interactions are taking place considered over the entire cycle is less than or equal to zero (for a reversible cycle).