Entropy

1. 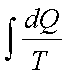has the same value irrespective of path as long as path is reversible

2. 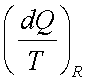is an exact differential of some function which is identical as entropy

3.

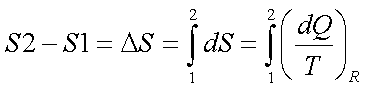
4. 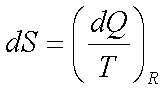for reversible process only

Calculation of Entropy change

1. Entropy is a state function. The entropy change is determined by its initial and final states only

2. In analyzing irreversible process, it is not necessary to make a direct analysis of actual reversible process.

Substitute actual process by an imaginary reversible process. The entropy change for imaginary reversible process is same as that of an irreversible process between given final and initial states.

(a) Absorption of energy by a constant temperature reservoir

Energy can be added reversibly or irreversibly as heat or by performing work.

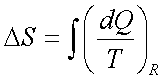
Example:-

The contents of a large constant-temperature reservoir maintained at 500 K are continuously stirred by a paddle wheel driven by an electric motor. Estimate the entropy change of the reservoir if the paddle wheel is operated for two hours by a 250W motor.

Paddle wheel work converted into internal energy- an irreversible process. Imagine a reversible process with identical energy addition

(b) Heating or cooling of matter

for constant volume heating

for constant pressure heating

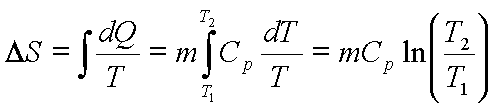
, for constant pressure

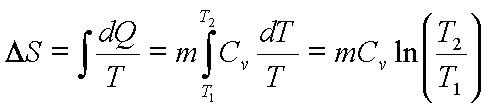
, for constant volume process

Example: -

Calculate entropy change if 1kg of water at 30⁰ C is heated to 80⁰C at 1 bar pressure. The specific heat of water is 4.2kJ/kg-K

(c) Phase change at constant temperature and pressure

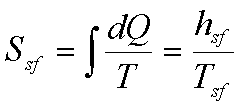
Example:-

Ice melts at 0⁰C with latent heat of fusion= 339.92 kJ/kg. Water boils at atmospheric pressure at 100⁰C with h_fg= 2257 kJ/kg.

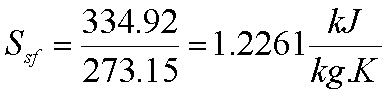
(d) Adiabatic mixing

Example:-

A lump of steel of mass 30kg at 427⁰ C is dropped in 100kg oil at 27⁰C.The specific heats of steel and oil is 0.5kJ/kg-K and 3.0 kJ/kg-K respectively. Calculate entropy change of steel, oil and universe.

T= final equilibrium temperature.

or T=319K

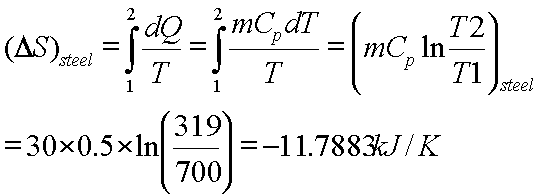
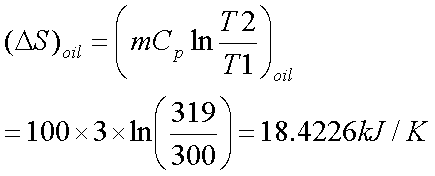
Tds relations

From the definition of entropy,

dQ = Tds

From the first law of thermodynamics,

dW = PdV

Therefore,

TdS = dU + PdV

Or, Tds = du + Pdv

This is known as the first Tds or, Gibbs equation.

The second Tds equation is obtained by eliminating du from the above equation using the definition of enthalpy.

h = u + Pv à dh = du + vdP

Therefore, Tds = dh – vdP

The two equations can be rearranged as

ds = (du/T) + (Pdv/T)

ds = (dh/T) – (vdP/T)

Change of state for an ideal gas

If an ideal gas undergoes a change from P₁, v₁, T₁ to P₂, v₂, T₂ the change in entropy can be calculated by devising a reversible path connecting the two given states.

Let us consider two paths by which a gas can be taken from the initial state, 1 to the final state, 2.

The gas in state 1 is heated at constant pressure till the temperature T₂ is attained and then it is brought reversibly and isothermally to the final pressure P₂.

Path 1-a: reversible, constant-pressure process.

Path a-2: reversible, isothermal path

Ds_1-a = òdq/T = òC_p dT/T = C_p ln(T₂/T₁)

Ds_a-2 = òdq/T = ò(du+Pdv)/T = ò(Pdv)/T = Rln(v₂/v_a)

(Since du = 0 for an isothermal process)

Since P₂v₂ = P_av_a = P₁v_a

Or, v₂/v_a = P₁/P₂

Or, Ds_a-2 = -Rln(P₂/P₁)

Therefore, Ds = Ds_1-a + Ds_a-2

= C_p ln(T₂/T₁) – Rln(P₂/P₁)

Path 1-b-2: The gas initially in state 1 is heated at constant volume to the final temperature T₂ and then it is reversibly and isothermally changed to the final pressure P₂.

1-b: reversible, constant volume process

b-2: reversible, isothermal process

Ds_1-b = C_v ln(T₂/T₁)

Ds_b-2 =Rln(v₂/v₁)

or, Ds = C_v ln(T₂/T₁)+ Rln(v₂/v₁)

The above equation for Ds can also be deduced in the following manner:

ds = (dq/T)_R = (du + Pdv)/T = (dh – vdP)/T

or,