Thermodynamic relations
Gibbs Function and Helmoltz Function
Gibbs equation is
du = Tds - Pdv
The enthalpy h can be differentiated,
dh = du + pdv + vdP
Combining the two results in
dh = Tds + vdP
The coefficients T and v are
partial derivative of h(s,P),
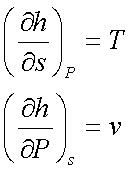
Since v > 0, an
isentropic increase in pressure will result in an increase in enthalpy.
We introduce Helmholtz
function
a = u – Ts
Combine Gibbs equation with
the differential of a,
da = -Pdv – sdT
The coefficient –P and –s
are the partial derivatives of f(v,T), so
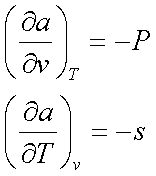
Similarly, using the Gibbs
function
g = h – Ts
dg = vdP – sdT
Consequently,
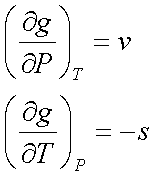
Note:
1. The decrease in Helmholtz function of a system sets an upper limit to the work done in any process between two equilibrium states at the same temperature during which the system exchanges heat only with a single reservoir at this temperature. Since the decrease in the Helmholtz potential represents the potential to do work by the system, it is also a thermodynamic potential.
2. The decrease in Gibbs function of a system sets an upper limit to the work, exclusive of “pdv” work in any process between two states at the same temperature and pressure, provided the system exchanges heat only with a single reservoir at this temperature and that the surroundings are at a constant pressure equal to that in the end states of the pressure.
The maximum work is done
when the process is isothermal isobaric. Gibbs function is also called Chemical
Potential.
Some important property relations
dz(x,y) = Mdx + Ndy
where, M = 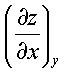 N =
N = 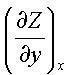
Mathematically, we would say
that dz is an exact differential, which simply means that z is a
continuous function of the two independent variables x and y. Since the order
in which a second partial derivative is taken is unimportant, it follows that,
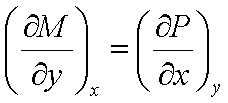
Maxwell’s
relations:
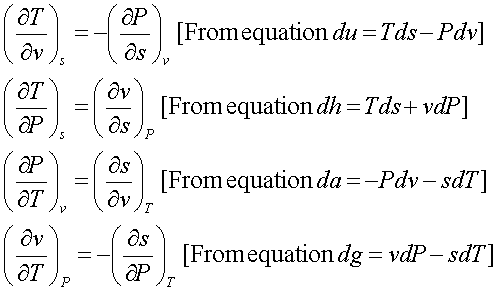
Mnemonic Diagram
The differential expressions for the thermodynamic potentials and Maxwell relations can be remembered conveniently in terms of a thermodynamic Mnemonic diagram.
The diagram consists of a
square with two diagonal arrows pointing upwards and the thermodynamic
potentials in alphabetical order clockwise on the sides as shown in figure. The
natural variables associated with each potential are placed in the corners.

Diagonal arrows indicate the
coefficients associated with the natural variables in the differential
expression of the potential. The sign of the coefficient depends on whether the
arrow is pointing towards (- ve) or away from the natural variable (+ ve).
For example,
du =
(sign)(coeff.) ds + (sign)(coeff.) dv
du = (sign)Tds +
(sign)Pdv
du = +Tds - Pdv
To write the Maxwell
relations we need to concentrate on the direction of the arrows and the natural
variables only.
If both the arrows pointing
in the same direction, there is no need to change the sign, otherwise the
equation should carry a negative sign.
The internal energy
u = u(T,v)
For a simple compressible
substance,

Taking entropy as a function of temperature and volume,
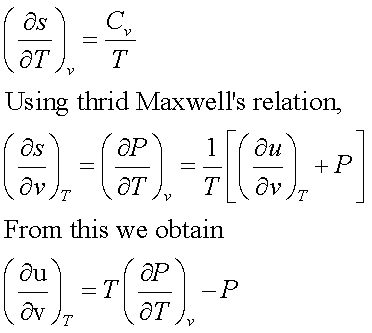
This important equation expresses the dependence of the internal energy on the volume at fixed temperature solely in terms of measurable T, P and v. This is helpful in construction of tables for u in terms of measured T, P and v.
For a perfect gas,
Pv = RT
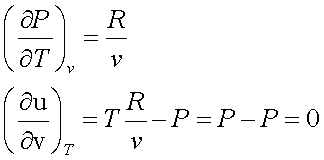
This implies that, for a perfect gas, internal energy is independent of density and depends only on T.
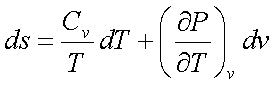
Similarly it can be shown using Fourth Maxwell’s relation that
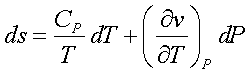
Using the above two equations and solving for dP,
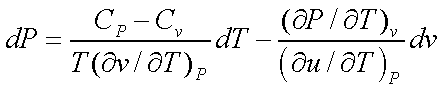
Considering P as a function of T and v, we see that
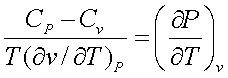
Two thermodynamic properties
can be defined at this stage,
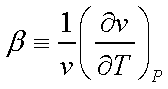
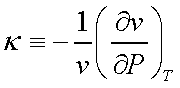
b is called the isobaric
compressibility and k is called the isothermal compressibility.
From calculus, it can be
shown that,
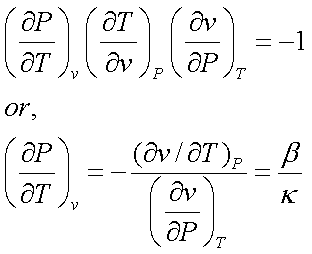
Therefore,
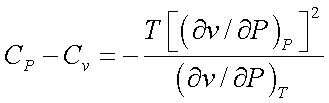
Since ![]() is always negative for all stable substances, CP
is always greater that Cv
is always negative for all stable substances, CP
is always greater that Cv