Available and
Unavailable Energy
The second law of
thermodynamics tells us that it is not possible to convert all the heat
absorbed by a system into work.
Suppose a certain quantity
of energy Q as heat can be received from a body at temperature T.
The maximum work can be
obtained by operating a Carnot engine (reversible engine) using the body at T
as the source and the ambient atmosphere at T0 as the sink.
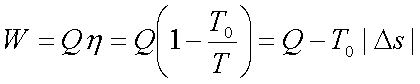
Where Ds is the entropy of the body
supplying the energy as heat.
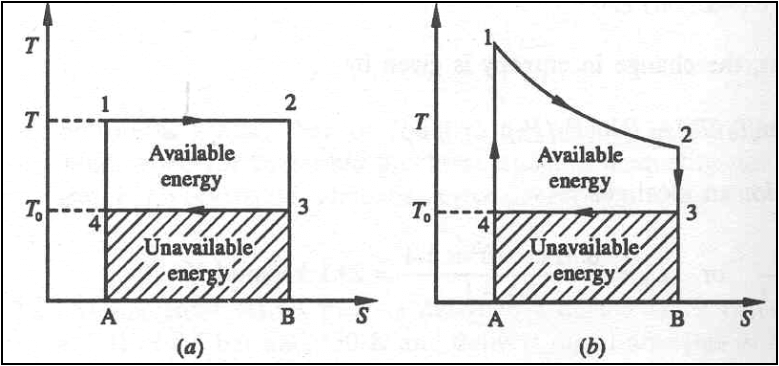
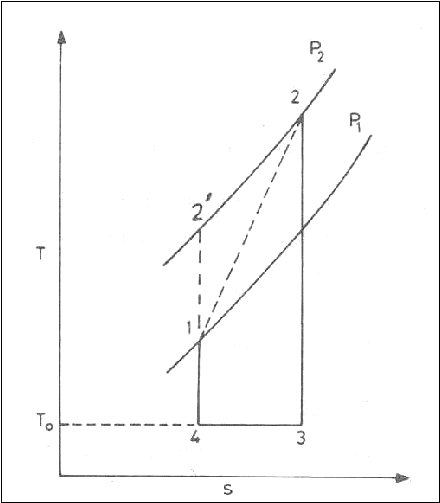
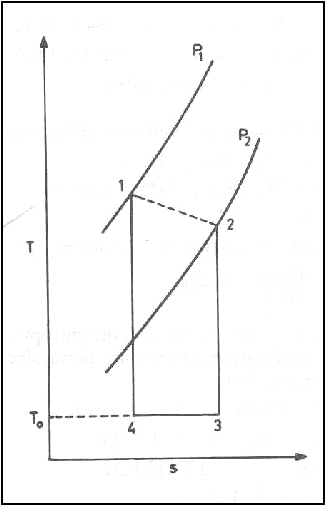
The Carnot cycle and the
available energy is shown in figure.
The area 1-2-3-4 represents
the available energy.
The shaded area 4-3-B-A
represents the energy, which is discarded to the ambient atmosphere, and this
quantity of energy cannot be converted into work and is called Unavailable
energy.
Suppose a finite body is
used as a source. Let a large number of differential Carnot engines be used
with the given body as the source.
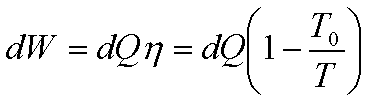
If the initial and final
temperatures of the source are T1 and T2 respectively,
the total work done or the available energy is given by
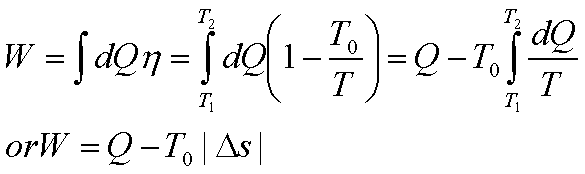
Loss in Available Energy
Suppose a certain quantity
of energy Q is transferred from a body at constant temperature T1 to
another body at constant temperature T2 (T2<T1).
Initial available energy,
with the body at T1,
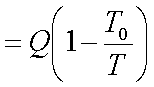
Final available energy, with
the body at T2,

Loss in available energy
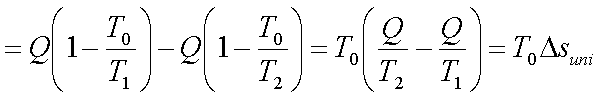
where Dsuni is the
change in the entropy of the universe.
Availability Function
The availability of a given
system is defined as the maximum useful work that can be obtained in a
process in which the system comes to equilibrium with the surroundings or
attains the dead state.
(a) Availability Function
for Non-Flow process:-
Let P0 be the
ambient pressure, V1 and V0 be the initial and final
volumes of the system respectively.
If in a process, the system
comes into equilibrium with the surroundings, the work done in pushing back the
ambient atmosphere is P0(V0-V1).
Availability= Wuseful=Wmax-P0(V0-V1)
Consider a system which
interacts with the ambient at T0. Then,
Wmax=(U1-U0)-T0(S1-S0)
Availability= Wuseful=Wmax-P0(V0-V1)
= ( U1-T0 S1)- ( U0-T0
S0)- P0(V0-V1)
= ( U1+ P0V1-T0
S1)- ( U0+P0V0-T0 S0)
= f1-f0
where f=U+P0V-T0S
is called the availability function for the non-flow process. Thus, the
availability: f1-f0
If a system undergoes a
change of state from the initial state 1 (where the availability is (f1-f0) to the final
state 2 (where the availability is (f2-f0), the change in
the availability or the change in maximum useful work associated with the
process, is f1-f2.
(b) Availability Function
for Flow process:-
The maximum power that can
be obtained in a steady flow process while the control volume exchanges energy
as heat with the ambient at T0, is given by:
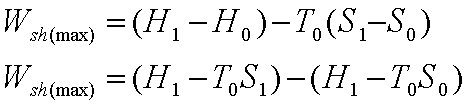
Sometimes the availability
for a flow process is written as:

which is called the Darrieus
Function.
Second Law Efficiency
The second law efficiency (h2) of a process,
h2=Change in the
available energy of the system
------------------------------------------------------
Change in the available energy of the source
 (a) Compressors
and Pumps:-
(a) Compressors
and Pumps:-
Change in the availability
of the system is given by:

where T0 is the
ambient temperature
The second law efficiency of
a compressor or pump is given by,

(b) Turbines and Expanders:-
The change in the available
energy of the system=W
The change in the available
energy of the source=Wrev=B1-B2
The second law efficiency of
the turbine h2T/E is given by,
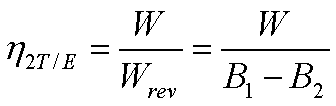
Work Potential Associated with Internal Energy
The total useful work
delivered as the system undergoes a reversible process from the given state to
the dead state (that is when a system is in thermodynamic equilibrium with the
environment), which is Work potential by definition.
Work Potential = Wuseful=
Wmax- P0(V0-V1)
= ( U1-T0 S1)- ( U0-T0
S0)- P0(V0-V1)
= ( U1+ P0V1-T0
S1)- ( U0+P0V0-T0 S0)
= f1-f0
The work potential of
internal energy (or a closed system) is either positive or zero. It is never
negative.
Work Potential Associated with Enthalpy,h
The work potential
associated with enthalpy is simply the sum of the energies of its components.
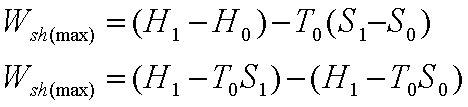
The useful work potential of
Enthalpy can be expressed on a unit mass basis as:
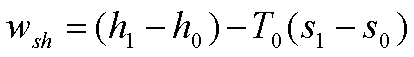
here h0 and s0
are the enthalpy and entropy of the fluid at the dead state. The work potential
of enthalpy can be negative at sub atmospheric pressures.