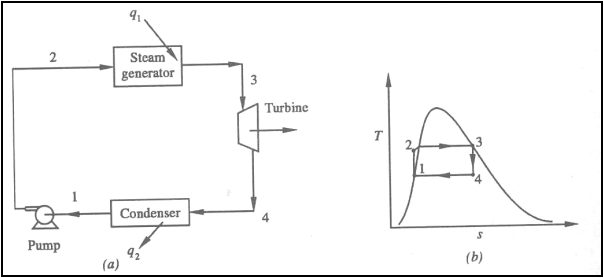
Ideal Rankine Cycle
(a) Schematic representation
of an ideal Rankine cycle (b) T-s diagram of an ideal Rankine cycle
Application of the First law
of thermodynamics to the control volume (pump, steam generator, turbine and
condenser), gives
Work done on pump, per kg of
water, WP= h2-h1
Energy added in steam
generator, q1= h3-h2
Work delivered by turbine, WT= h3-h4
Energy rejected in the
condenser, q2= h4-h1
The thermal efficiency of
the Rankine cycle is given by,
h= Net work done
----------------------
Energy absorbed
Practical Rankine cycle
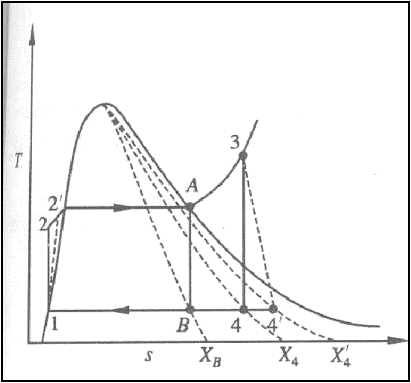
Pump and Turbine do not
operate isentropically in practice.
The practical Rankine cycle
is shown as 1-2’-3-4’-1.
In the actual turbine, the
work delivered is less than the isentropic turbine. Similarly, the work
consumed by an actual pump is greater than the work consumed by an isentropic
pump.
That is,
h3-h4’
< h3-h4
h2’-h1
> h2-h1
Thermal efficiency of a
practical Rankine cycle,
The performance of an actual
turbine or pump is usually expressed in terms of isentropic efficiency.
Isentropic efficiency of
turbine (hT) is defined as
the ratio of ‘Work delivered by actual turbine’ to ‘Work delivered by an
isentropic turbine’.
Isentropic efficiency of
pump (hP) is defined as
the ratio of ‘Work required by
isentropic pump’ to ‘Work required by actual pump’
Methods to increase the efficiency of the Rankine cycle
Basic idea: Increase the average temperature at which heat is transferred to the working fluid in the boiler, or decrease the average temperature at which heat is rejected from the working fluid in the condenser.
1. Lowering the condenser
Pressure:-
Lowering the operating
pressure of the condenser lowers the temperature at which heat is rejected. The
overall effect of lowering the condenser pressure is an increase in the thermal
efficiency of the cycle.
2. Superheating the steam
to high temperatures:-
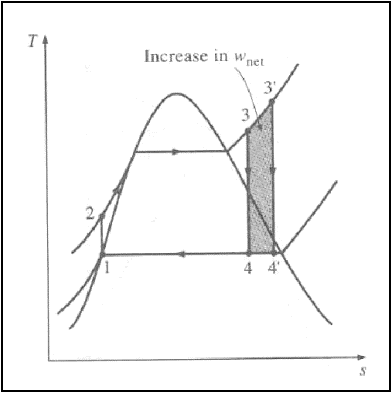
The average temperature at
which heat is added to the steam can be increased without increasing the boiler
pressure by superheating the steam to high temperatures.
Superheating the steam to
higher temperatures has another very desirable effect: It decreases the
moisture content of the steam at the turbine exit.
3. Increasing the Boiler
pressure:-
Increasing the operating
pressure of the boiler, automatically raises the temperature at which boiling
takes place.
This raises the average temperature
at which heat is added to the steam and thus raises the thermal efficiency of
the cycle..
Reheat Rankine Cycle
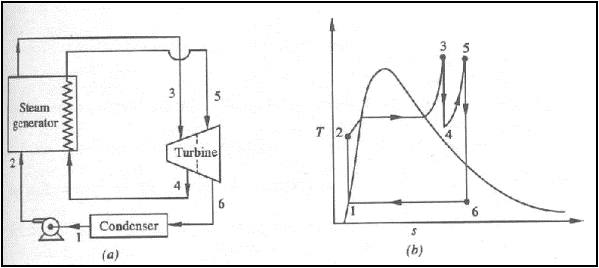
(a) schematic representation
of a reheat Rankine cycle (b) T-s diagram of a reheat Rankine cycle
The energy added ( per unit
mass of steam ) in the steam generator is given by,
The energy rejected in the
condenser,
The thermal efficiency,
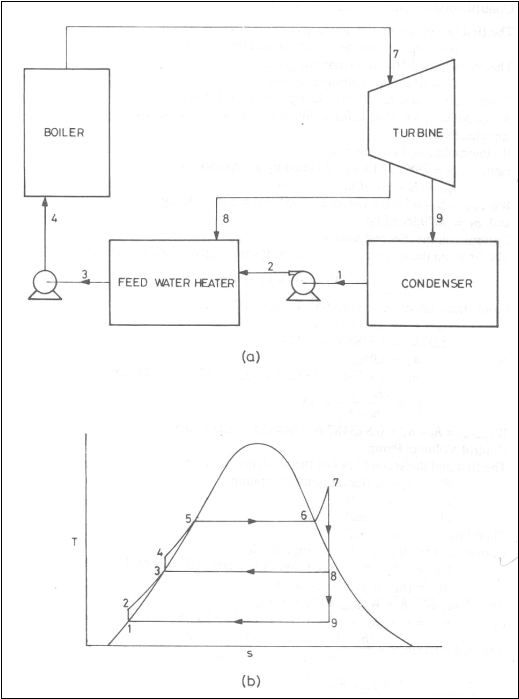Regenerative Cycle
(a)
schematic diagram (b) T-s diagram
Consider the feed water
heater as the control volume and apply the first law of thermodynamics to
obtain,
and 
or 
or 
Let, 
=Y’= the fraction of steam extracted
from the turbine for preheating
Energy added in the boiler
per unit mass of the working fluid,
Energy rejected in the
condenser,
Thermal efficiency,
The work output of the
turbines =
Work spent on the pumps =
Air standard Otto Cycle
Air standard Otto
cycle on (a) P-v diagram (b) T-s diagram
Processes: -
0-1: a fresh mixture of
fuel-air is drawn into the cylinder at constant pressure
1-2: isentropic compression
2-3: energy addition at
constant volume
3-4: isentropic expansion
4-1: combustion products
leave the cylinder
1-0: the piston pushes out
the remaining combustion products at constant pressure
Since the net work done in
processes 0-1 and 1-0 is zero, for thermodynamic analysis, we consider the
1-2-3-4 only.
The thermal efficiency of
the cycle is given by
where Q1 and Q2
denote the energy absorbed and rejected as heat respectively.
For a constant volume
process Q=DU. If ‘m’ is the
mass of the air which is undergoing the cyclic process,
Energy is absorbed during
the process 2-3
Energy is rejected during
the process 4-1
Hence,
For an ideal gas undergoing
an isentropic process (process 1-2 and 3-4),
= constant
Hence,
and 
But v1=v4
and v2=v3. Hence we get,
or 
or 
Hence, 
Where the
compression ratio r0 is defined as
Sometimes it is
convenient to express the performance of an engine in terms of Mean
effective Pressure, Pm, defined as the ratio of “Net work done”
to “Displacement volume”
Thermal efficiency of the ideal Otto cycle as a function of compression ratio (g=1.4)
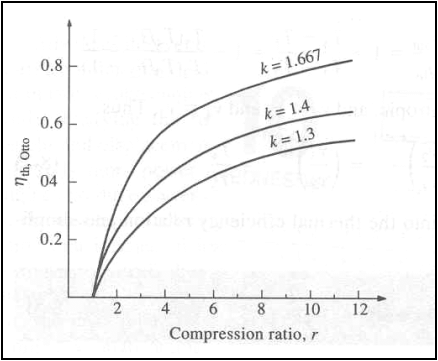
The thermal efficiency of the Otto cycle increases with the specific
heat ratio, g of the working
fluid.
Air standard Diesel cycle
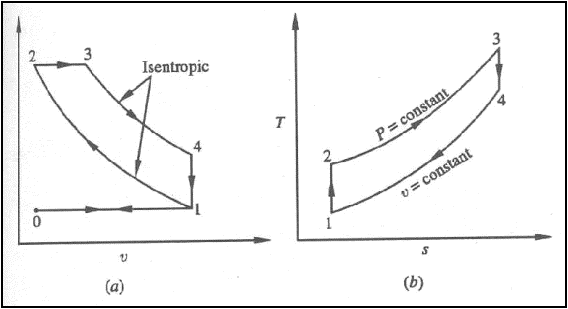
Diesel cycle on (a) P-v
diagram (b) T-s diagram
Processes: -
0-1: fresh air is drawn into
the cylinder
1-2: isentropic compression
2-3: constant pressure
energy addition
3-4: isentropic expansion
4-1: combustion products
leave the cylinder
1-0: remaining combustion
products are exhausted at constant pressure
Defining cutoff ratio, rc
as,
For a constant pressure
process (2-3),
Q=DH.
Hence, the energy addition
during process 2-3,
where ‘m’ is the mass of gas
undergoing the cyclic change.
The energy rejection during
the process 4-1,
The thermal efficiency, h is given by
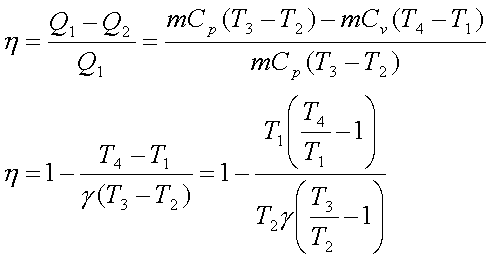
Since the process 1-2 is
isentropic,
Since the process 4-1 is a
constant volume process,
since P2=P3
The processes 1-2 and 3-4
are isentropic. Hence,
and 
Hence we get,
For the constant pressure
process,
Hence the efficiency
becomes,
The mean effective pressure
of an air standard diesel cycle is given by,
Thermal efficiency of the
ideal diesel cycle as a function of compression and cutoff ratios (g=1.4)
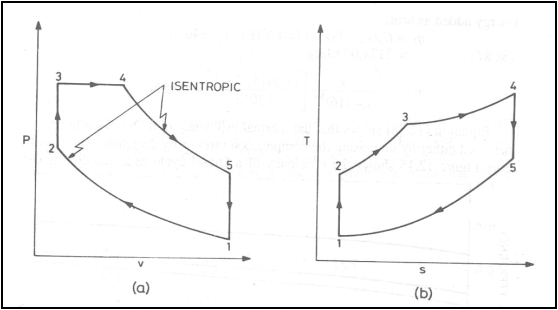Air standard Dual cycle
Dual cycle on (a) P-v
diagram (b) T-s diagram
Energy addition is in two
stages: Part of energy is added at constant volume and part of the energy is
added at constant pressure
Energy added, q1
Energy rejected, q2
Thermal efficiency, h
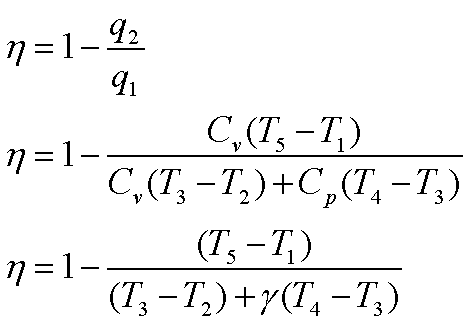
The efficiency can be
expressed also in terms of,
Compression ratio, r0 = V1/V2
Cut-off ratio, rc = V4/V3
Constant volume pressure
ratio, rvp= P3/P2