(b) Conservation of Energy applied to a Control Volume
Let 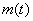 = total mass inside the CV at time = total mass inside the CV at time 
 total mass inside the CV at time total mass inside the CV at time 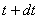
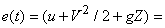 specific energy of matter inside the control volume at time t specific energy of matter inside the control volume at time t
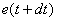 = specific energy of matter inside the control volume at time = specific energy of matter inside the control volume at time 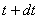
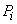 and and 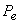 = Pressure at the inlet and exit ports respectively = Pressure at the inlet and exit ports respectively
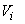 and and 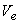 = Flow velocity at the inlet and exit ports respectively = Flow velocity at the inlet and exit ports respectively
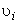 and and 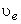 = specific volumes at the inlet and exit ports respectively = specific volumes at the inlet and exit ports respectively
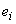 and and 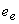 = specific energy of the material at the inlet and exit ports respectively = specific energy of the material at the inlet and exit ports respectively
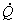 = Rate energy flow as heat into the control volume = Rate energy flow as heat into the control volume
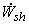 = Rate of shaft work done by the control volume = Rate of shaft work done by the control volume
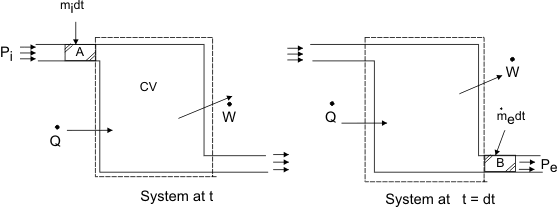
The mass contained in the region A which enters the control volume during the time interval 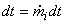
The mass contained in the region B which leaves the control volume during the time interval 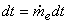
From the mass balance, we can write
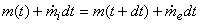 |
(12.6) |
where 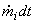 is the mass entering the control volume during the differential time is the mass entering the control volume during the differential time  . To accommodate this, the mass inside the control volume has to be compressed such that its volume decreases by the amount . To accommodate this, the mass inside the control volume has to be compressed such that its volume decreases by the amount 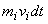 . This is accomplished by the pressure . This is accomplished by the pressure 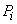 acting on the material entering the control volume. Therefore, the work done = acting on the material entering the control volume. Therefore, the work done = 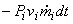
Since the mass 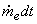 has to leave the control volume at the exit port, the work done = has to leave the control volume at the exit port, the work done = 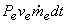 , ,
Energy of the system at time 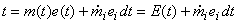
Energy of the system at time 
During the time interval  We may account for the following We may account for the following
Energy transferred as heat to the system = 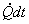
Shaft work done by the system 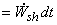
Energy flow as heat into the control volume and the shaft work delivered by the control volume are taken as positive. By applying the first law of thermodynamics, we get
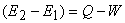 |
(12.7) |
or,
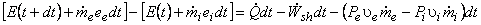 |
(12.8) |
or,
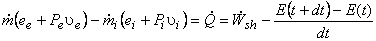 |
(12.9) |
In the limiting case, 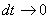
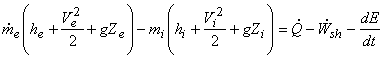 |
(12.10) |
Where,
 and and 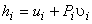 |
|
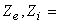 elevation of the exit and inlet ports above the datum level. The above expression can now be rearranged as elevation of the exit and inlet ports above the datum level. The above expression can now be rearranged as
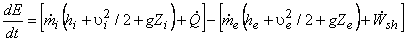 |
(12.11) |
Rate of energy accumulation = Rate of energy inflow - Rate of energy outflow
|