Charging of a Cylinder (control Volume Analysis)
While charging the cylinder from the supply mains, no gas leaves the control volume, and 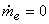 . No shaft work is done; . No shaft work is done;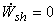 . Let us ignore the changes in the kinetic energy and potential energy of the gas during charging operation. Then it is possible to write from the equation (15.1) . Let us ignore the changes in the kinetic energy and potential energy of the gas during charging operation. Then it is possible to write from the equation (15.1)
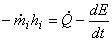 |
(15.2) |
or,
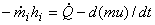 |
(15.3) |
Where, 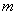 denotes the mass of the gas in the control volume and denotes the specific internal energy of the gas inside the control volume at time denotes the mass of the gas in the control volume and denotes the specific internal energy of the gas inside the control volume at time 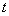 . It is assumed that the state of the gas at any instant of time inside the control volume is uniform. The expression above can be integrated from the start of the charging operation . It is assumed that the state of the gas at any instant of time inside the control volume is uniform. The expression above can be integrated from the start of the charging operation 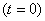 to the end of the charging operation to the end of the charging operation 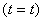 , to obtain , to obtain
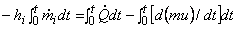 |
(15.4) |
The principles of conservation of mass for the charging process reduces to:
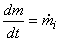 |
(15.5) |
Rate of increase of mass in 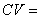 Rate of mass entry Rate of mass entry
Integration of the above equation over time 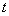 gives the change of mass in the control volume during the charging operation gives the change of mass in the control volume during the charging operation
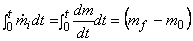 |
(15.6) |
Now in the energy (15.4), the last term on the RHS can be evaluated as
 |
(15.7) |
and
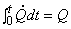 |
(15.8) |
Substituting (15.6), (15.7), and (15.8) in (15.4) we get
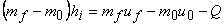 |
(15.9) |
If the cylinder is initially empty and the filling operation is carried out under adiabatic conditions the first law expression reduces to
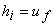 |
(15.10) |
If the gas is treated as ideal 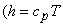 and and 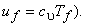
Then,
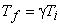 |
(15.11) |
Where, 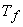 is the final temperature of the gas in the cylinder and is the final temperature of the gas in the cylinder and 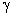 is the ratio of the specific heats. is the ratio of the specific heats. 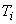 is the temperature of the supply mains. is the temperature of the supply mains.
|