Case of an Ideal Gas
Consider a small amount of gas in the cylinder (confined in an imaginary envelope) in the cylinder as a system.
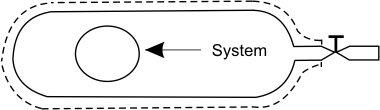
Figure 15.3
Imagine a situation when gas escapes the cylinder.
The boundary of the system changes continuously and eventually occupies the entire volume of the cylinder. The gas which is left in the cylinder does not exchange energy in the form of heat with the surroundings. It undergoes an adiabatic expansion. We can prove that the gas undergoes a reversible adiabatic expansion.
The general expression is:
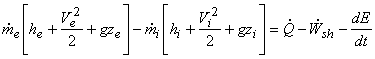 |
(15.21) |
We can change the basis of analysis from a control mass to a control volume based analysis. Under such a situation, Let us consider the cylinder volume as the volume of interest.
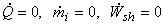 , and ignore the change in KE and PE , and ignore the change in KE and PE
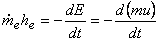 |
(15.22) |
From the principle of conservation of mass
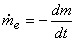 |
(15.23) |
Therefore
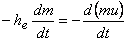 |
(15.24) |
For a perfect gas, 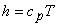 and and 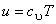
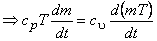 |
(15.25) |
or,
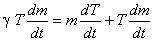 |
(15.26) |
or,
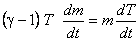 |
(15.27) |
or,
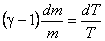 |
(15.28) |
By integration between final state and initial state
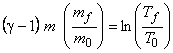 |
(15.29) |
As
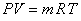 |
(15.30) |
or,
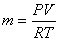 |
(15.31) |
Where 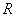 is the characteristics gas constant is the characteristics gas constant
So,
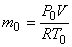 |
(15.32) |
and
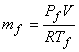 |
(15.33) |
Invoking these relations, we gas
 |
(15.34) |
or,
The gas that remains in the tank can be considered to have undergone a reversible adiabatic expansion from the initial pressure 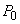 to the final pressure to the final pressure  . .
|