Research
My work is focused on numerical simulation of turbulent flows. As part of my research, I developed an open-source finite-difference solver, SARAS. The solver is presently being used to simulate turbulence in Rayleigh-Bénard convection (RBC), and rotating flows. Moreover, a Large-Eddy Simulation (LES) model was also implemented as an additional module in SARAS.
Rayleigh Bénard Convection
Rayleigh-Bénard convection (RBC) uses a deceptively simple setup to demonstrate a rich kaleidoscope of fluid phenomena. From steady laminar flows, to oscillating rolls, to wildly chaotic turbulence, the whole gamut of fluid dynamics can be captured in RBC. Here, the fluid is confined between two plates - hot plate at the bottom and cold plate at the top. Buoyancy is the engine that drives the flow - the force of gravity pulls the denser, colder fluid from the top, while the warmer, lighter fluid displaced from the bottom plate rise as plumes.
The non-dimensional parameter, Rayleigh number, is used to quantify the strength of buoyancy. Increasing the Rayleigh number tends to drive the convection faster, and thereby make the flow more turbulent.
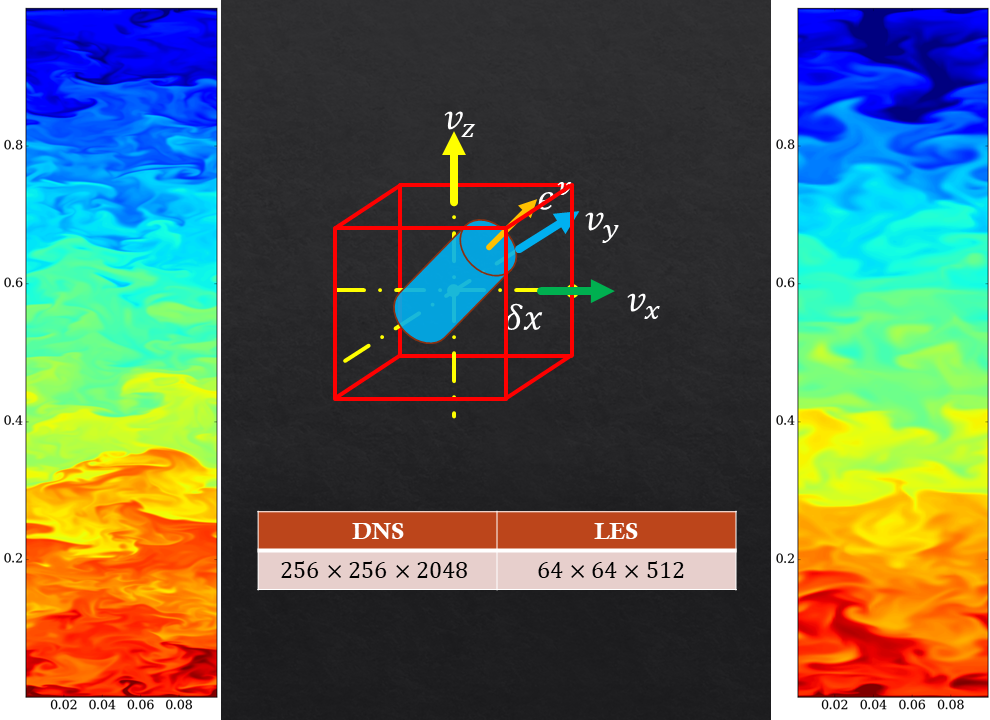
To the right is a plot of the temperature field along a vertical cross-section of an RBC simulation. The flow is evolving at a high Ra of \(4.0 \times 10^9\). The simulation was performed using SARAS on a 10243 grid. The solver used 4096 cores of the Shaheen II supercomputer at the King Abdullah University of Science (KAUST), Saudi Arabia, to generate this solution.
We can easily notice the plumes of hot fluid rising from the bottom, as jets of cold fluid simultaneously fall from the top wall. The domain is periodic along both the horizontal directions.

Large Eddy Simulation
Perhaps the most enduring aspect of turbulence is its multi-scale nature. In fully turbulent flows, the fluid swirls around in eddies of a wide range of sizes. As a result, direct simulations of such flows require very fine grids with millions of grid points. Large Eddy Simulations relieve this constraint by limiting the finest resolved scales and relying on mathematical models to predict what happens at the sub-grid scales.
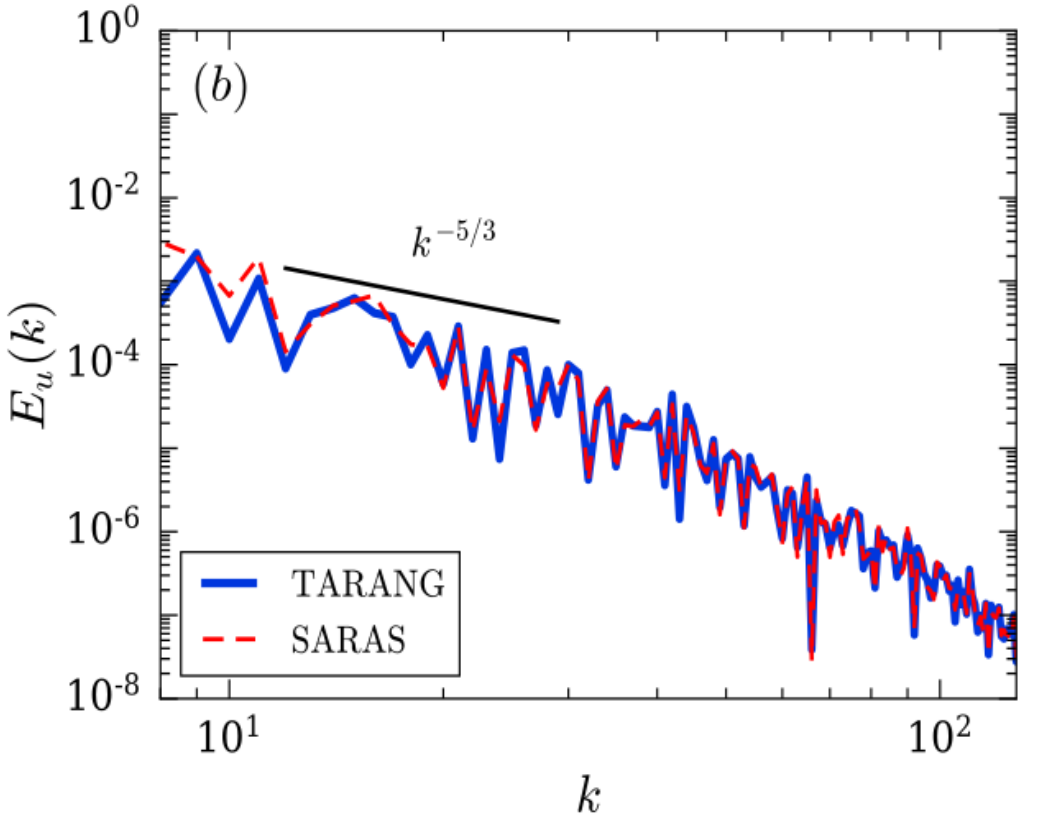
One method of predicting the effect of unresolved scales is to use an additional turbulent viscosity. There exists a wide variety of models to calculate this additional viscosity, and one such method is to use renormalization group theory to compute a renormalized viscosity. This method was implemented in the pseudo-spectral code, TARANG, and used to simulate both hydrodynamic and convective turbulence.
Presently I am using the stretched-spiral vortex model to compute the sub-grid stress. This method was used to simulate RBC at very high Rayleigh numbers.
SARAS
SARAS is an open-source finite-difference fluid solver written in C++. The solver is parallelized using MPI and is capable of solving hydrodynamic and convective turbulence. Thanks to its modular structure, which makes use of object oriented design, the solver can be readily adapted to use custom boundary conditions, initial conditions, and forcing terms.
The solver offers 2nd order and 4th order explicit finite-difference stencils to calculate derivatives. Moreover, there is the option to choose from 2nd order Crank-Nicholson scheme or 3rd order low-storage Runge-Kutta scheme for integration of PDEs. The stretched spiral vortex LES model described above is also an add-on to SARAS.
The solver is available for download on GitHub, and a brief description of its capabilities is available in this paper at the Journal of Open Source Software.
Compressible Flow Solver
During my stint as Project Scientist at the High Performance Computing Lab (HPCL) at the Department of Aerospace Engineering, IIT-Kanpur, I developed an MPI-parallelized 3D compressible flow solver in FORTRAN. The solver uses the Optimized Upwind Compact Scheme-3 (OUCS3) to compute spatial derivatives, and an optimized three-stage Runge-Kutta scheme for time-integration.
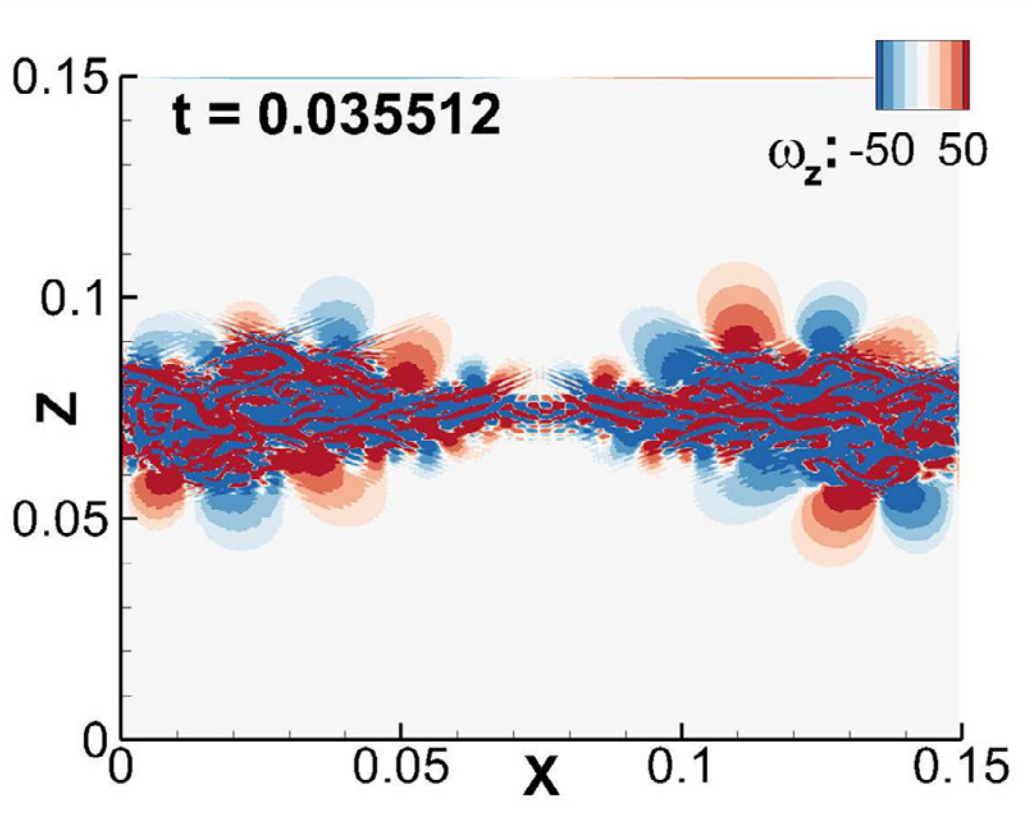
Although the solver was originally written for a generalized curvilinear coordinate system to simulate flow around a bluff body, it was subsequently modified to simulate Rayleigh Taylor Instability (RTI) in a much simpler cubic domain.
RTI starts off in an unstable configuration with a dense (cold) fluid at the top and a light (warm) fluid at the bottom, separated by a sharp interface. Subsequently, a difference in alignment of pressure and density gradients (baroclinic term) propagates and amplifies the instability, leading to the mixing of the two fluids. Here, the evolution of vorticity at the interface of two fluids is shown.
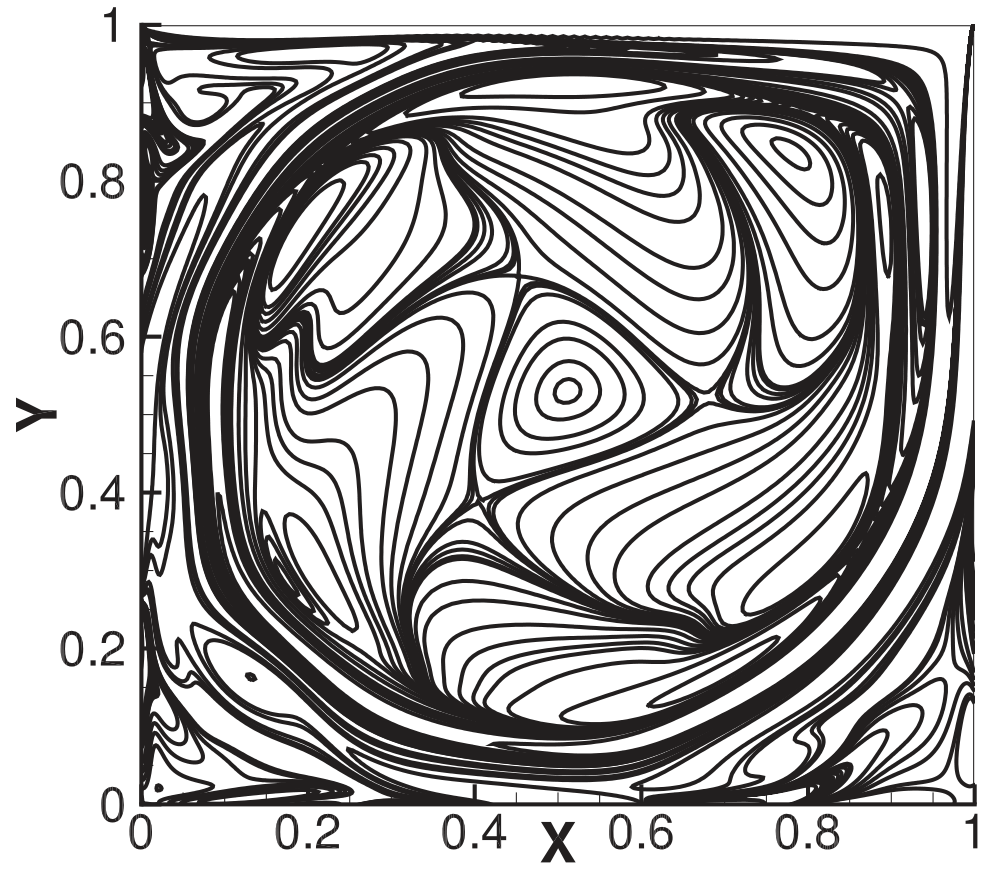
Compact Schemes
Compact schemes are finite-difference schemes that offer very high, spectral-like accuracy. In numerical simulations of fluid flows, we often have one of more variables (velocity, temperature, pressure, etc.) whose derivative must be computed. To do so, we first discretize the variable, say \(f\), on a grid, such that at the point \(i\) on the grid, its value is \(f_i\). Then we can use any finite-difference technique to get its derivatives, \(f_i'\). When we have a uniform grid such that \(x_{i+1} - x_i = \Delta x\), using compact schemes, we can write
$$ \alpha f'_{i-1} + \beta f'_i + \gamma f'_{i+1} = \frac{1}{\Delta x}\left(a f_{i-1} + b f_i + c f_{i+1}\right). $$When written for all \(i\), we get a system of linear equations, which can be written as a tridiagonal matrix. This matrix can be solved very quickly using Thomas algorithm. I worked on the implementation and testing of a similar compact scheme for non-uniform grids, called NUC6. Here, we see a snapshot of vorticity contours in lid-driven cavity (LDC) computed using NUC6 at a Reynolds number of 10,000.