If an optical field is deterministic, the interference caused by it has perfect visibility. However, fields produced by real sources are more or less random. The reason for this is that a real, physical source consists of infinitely many emitters all of which emit in a statistically independent manner. As a result the total field emitted by the source becomes random, in which case the interference occurs to the extent that the fields at two different space-time points are mutually correlated. The nature and the degree of this correlation is described through what is known as the coherence function, and the equation that dictates the dynamics of a coherence function is known as the Wolf equation. Coherence as a requirement for interference remains the same both in classical and quantum descriptions. This means that the two interfering field-amplitudes in the classical theory and the two interfering wave-functions in the quantum theory need to be mutually coherent for the interference to take place. Within quantum theory, the concept of coherence can also be cast in terms of the indistinguishability arguments. It says that if a photon in two separate interfering alternatives remain indistinguishable, that is, if there is no way of figuring out which particular interfering alternative a photon took then the two alternatives become mutually coherent and interference takes place between the two alternatives. We develop tools and techniques for characterizing and quantifying the coherence properties of classical and quantum light fields in various degrees of freedom.
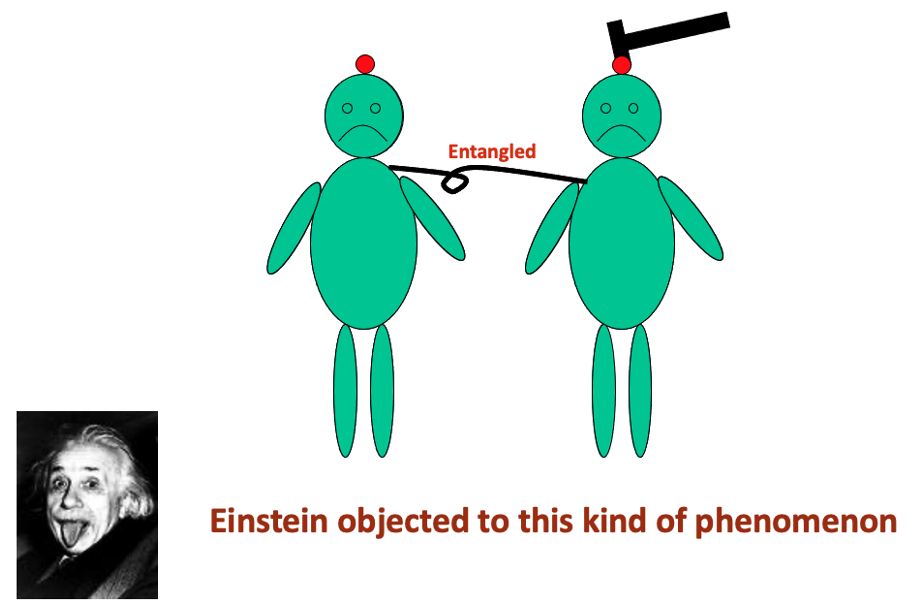
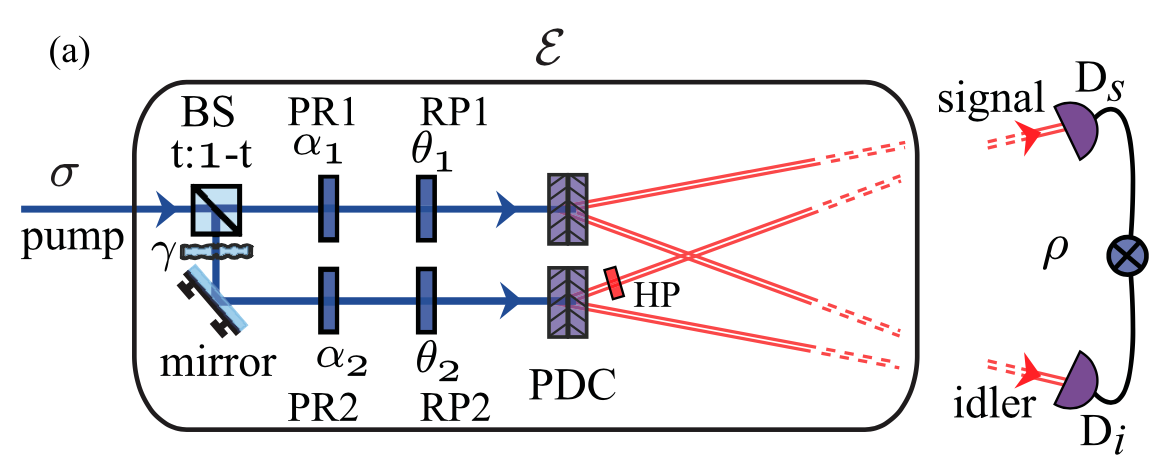
In 1935 A. Einstein, B. Podolsky, and N. Rosen recognized a spooky feature in the quantum description of physical reality. This feature, now known as entanglement, was originally called by Schrodinger “Verschrankung,” which implies the existence of global states of a composite system that cannot be described as a product of the states of the individual subsystems. Einstein, Podolsky and Rosen were explicitly considering a system of two entangled particles, which had once interacted in the past but had no interactions thereafter. They showed that in such a system, by measuring either the position or the momentum of one of the particles, either the position or the momentum of the other particle can be predicted with complete certainty without in any way disturbing the other particle. But, since position and momentum are non-commuting observables, they cannot be measured simultaneously and thus cannot be regarded as simultaneous elements of reality of a system. So they concluded that in entangled two-particles systems, the reality of position and momentum of the second system depend upon the process of measurement carried out on the first system, which does not disturb the second system in any way. On noting this apparent non-locality in the quantum theory, Einstein, Podolsky and Rosen argued that the quantum-mechanical description of physical reality is not complete and that it should be supplemented by postulating the existence of “hidden variables,” the specifications of which will predetermine the result of measuring any observable of the system. EPR’s inherent belief was that the predictions of quantum mechanics are correct but only as a consequence of the statistical distribution of hidden variables. Until mid 1990s, studies related to entanglement were mostly centered at probing the foundations of quantum mechanics. However, in recent years entanglement is beginning to be seen as a resource that could also be used for many useful applications. Some of these proposed applications include quantum cryptography, quantum dense coding, quantum teleportation, entanglement swapping, and quantum lithography. We study the generation and manifestation of entanglement and its intimate connections with coherence. For our experimental studies, we use entangled photons produced by the nonlinear optical process of parametric down-conversion [phase matching].
Reconstruction of a general quantum state is referred to as the quantum state tomography and is in general a very difficult experimental problem. This difficulty increases exponentially as the dimensionality of the unknown state increases. As a result, the experimental techniques employed for measuring a general quantum state are in general very inefficient. However, for certain classes of states, one can have relatively efficient measurement techniques. We have developed efficient measurement techniques for several classes of quantum states. Our approach of quantum state reconstruction is through the measurement of the coherence function. For example, we have shown that the quantum state reconstruction of states in the high-dimensional orbital angular momentum (OAM) basis can be efficiently carried out by measuring the angular coherence function of the field in an interferometer. This way, we have developed a very efficient method for measuring quantum state that have a diagonal density matrix representation. [Single-shot measurement of OAM, Angular Schmidt spectrum]. More recently, we have extended this approach for measuring the pure state in the OAM basis [Measurement of pure state]. Furthermore, we have used this approach for obtaining the states in the transverse momentum basis by measuring the spatial coherence function of the field [two-shot measurement of spatial coherence]. We are currently working on developing efficient schemes for measuring more generic class of quantum states in the high-dimensional bases.
Fields having partial spatial coherence have been extensively studied in the past few decades and have found a wide range of applications including wide-field optical coherence tomography (OCT) imaging through turbulence, optical communication, particle trapping, atomic optics, laser scanning, plasma instability suppression, photographic noise reduction, optical scattering, and second-harmonic generation. The existing experimental techniques for producing spatially partially coherent fields use a laser as the primary source, which, to begin with, is spatially a completely correlated source. One then tries to make the field emanating from such a source spatially partially coherent by introducing randomness in the field path by using either an acousto-optic cell, or a rotating ground glass plate (RGGP) or a spatial light modulator (SLM). We have been studying methods for producing spatially partially coherent field without having to introduce randomness from outside. In the context, we have demonstrated a technique for generating propagating-invariant spatially partially coherent field using a planar, spatially-completely-uncorrelated light-emitting diode (LED) placed at the back focal plane of a converging lens. By controlling the shape of the LED and adjusting the focal length of the lens, one can produce any desired propagating-invariant field [efficient generation]. We next demonstrated a technique that is based on the coherent mode decomposition of a partially coherent field. The coherent mode decomposition is a unique way of representing a partially coherent field as a mixture of the fully coherent modes. In our technique, we experimentally demonstrated generating Gaussian Schell-model field by mixing fully coherent Hermite-Gaussian modes [Generation of a GSM field]. In the context of generating partially coherent fields, the advantage of not introducing randomness from outside is that it provides a greater deal of control for generating fields customized for a given application.
Imaging through scattering media is a very important area of research due to its implications for a wide range of real-world applications. For example, imaging of objects at different transverse planes through atmospheric fog is inevitable in daily life scenarios such as railways, defence, and road trans- ports. Imaging through scattering media has been an important research problem since 1960s, and even today this a very active area of research. The difficulties in imaging through scattering media arise due to the inhomogeneities in such media which introduce random phase variations at different spatial locations in the light field passing through it. If the light field is spatially coherent, these random phase variations result in a random interference pattern known as the speckle pattern. As a consequence, what gets recorded is the image of the object superimposed with the speckle pattern at the imaging plane. Thus the recorded image gets corrupted and the image quality gets severely affected. Nonetheless, the speckle effect gets reduced if the light is spatially only partially coherent. By controlling the spatial coherence of the imaging field, we have developed various techniques for enhanced imaging capabilities in the presence of scattering and turbulent media [controlling propagation of spatial coherence]. Furthermore, we have shown that the structured spatially partially coherent fields are quite useful for communication in the presence of scattering and turbulent medium [structural robustness]. We are currently working on exploring partially coherent entangled two-photon fields for quantum metrology and quantum communication applications.
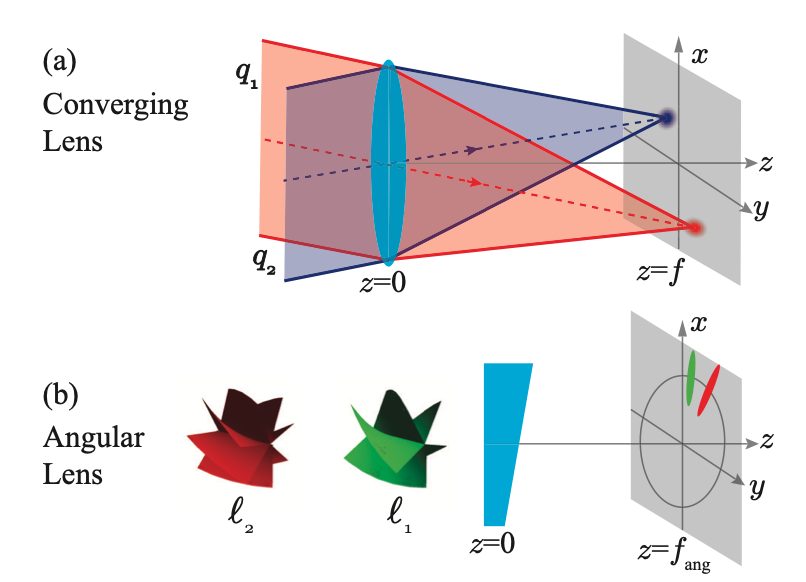
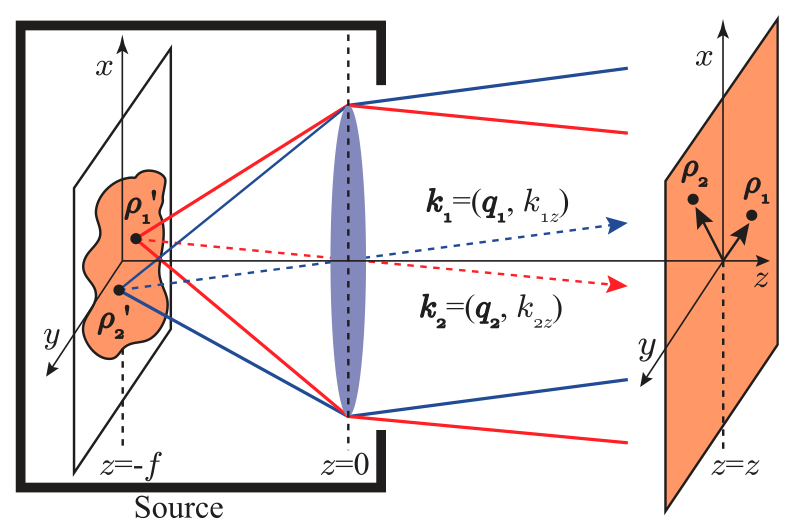
It is known that the tansverse position and the transverse wave-vector bases form a two-dimensional Fourier transform pair and that a converging lens is a phase-only optical element that performs this Fourier transformation. Owing to this transformation property of a lens, optical modes characterized by different transverse wave-vectors get mapped onto separated localized spots on a transverse plane after passing through a lens. When the aperture-size of the lens is infinite, the localized spots take the form of two-dimensional Dirac-delta functions and the wave-vector separation is said to be perfect. However, with a finite aperture-size lens, this separation is imperfect and its degree characterizes the resolving power of the lens. In a recent work, we have proposed and demonstrated a single phase-only optical element that separates out OAM modes into localized spots in much the same way as a converging lens separates out transverse wave-vector modes. We refer to this element as an “angular lens” and have shows that it provides a natural way of separating out OAM modes and can not only work with a large number of incoming modes but also at the single-photon level [angular lens]. An OAM-sorter based on only one phase-only element could be extremely useful for several OAM-based applications. We are currently working on improving the resolving power of our OAM sorter. We are further exploring the design of phase-only elements that could not only separate the OAM modes but also the entire two-dimensional set of transverse modes. With efficient sorter and detecors for orbital anguar momentum, we aim to explore high-dimensional OAM entanglement for quantum metrology applications.
The wave-particle duality, that is, the simultaneous existence of both particle and wave properties, is the most distinguishing feature of a quantum system. A quantum system is characterized in terms of physical quantities such as energy, momentum, etc., as well as in terms of correlations, the degree of which can be measured in terms of the contrast with which a system produces interference patterns. In the context of quantum systems consisting of more than one particle, the wave-particle duality can manifest as entanglement. Quantum entanglement refers to intrinsic multiparticle correlations in a system and is quite often referred to as the quintessential feature of quantum systems. There are many processes in which a quantum system gets annihilated to produce a new quantum system consisting of either equal or more number of particles. An example is the nonlinear optical process of parametric down-conversion (PDC), in which an input pump photon gets annihilated to produce two entangled photons called the signal and idler photons. However, it is not very well understood as to how in such processes the intrinsic correlations in the annihilated quantum system get transferred to the generated new quantum system. One of the main difficulties in addressing such questions is the lack of a mathematical framework for quantifying correlations in multidimensional systems in terms of a single scalar quantity, although more recently there have been a lot of research efforts with the aim of quantifying coherence. We have been studying how to quantify coherence in higher-dimensional system and find connections between the coherence and entanglement of high-dimensional systems. We have established a basis-independent definition for the degree of coherence for higher dimensional system. We refer to this as the intrinsic degree of coherence and it works for both discrete and continuous-variable bases [intrinsic degree of coherence]. We then extended this work for defining the intrinsic degree of coherence of a two-qubit state, which is a two-particle system, in which each particle lives in a two-dimensional Hilbert space [two-qubit intrinsic degree]. In this work, we also looked at how two-qubit coherence is connected to the two-qubit entanglement measures. In the context of parametric down-conversion, we have studied how the temporal coherence properties of the pump photon gets transferred and then manifest as the temporal coherence of the entangled two-photon field [transfer]. Furthermore, we have also investigated, how the degree of polarization of the pump photon puts an upper bound on the polarization entanglement of the generated two-qubit states [intrinsic upper bound]. Currently, we are working on connections between coherence and entanglement of multi-particle high-dimensional quantum states. We are also developing techniques for measuring the entanglement of multi-particle quantum states through coherence function measurements.