Interval Algebra
The concept of interval - algebra is borrowed
from the paper on Qualitative Reasoning of documents by Mukerjee
and Fujihara . The relative position of one point a point
with respect to another can be expressed as - , 0 , + , which distinguish
respectively precedence, coincidence and post-occurence. If one entity
is an interval and the other a point then one can define five zones : b
(coincide with back) , i (inside) , f (coincide with front ) , as well
as + and -. Relations between two intervals A and B can now be defined
as the 2-tuple of relations for the two endpoints of A with respect to
B.
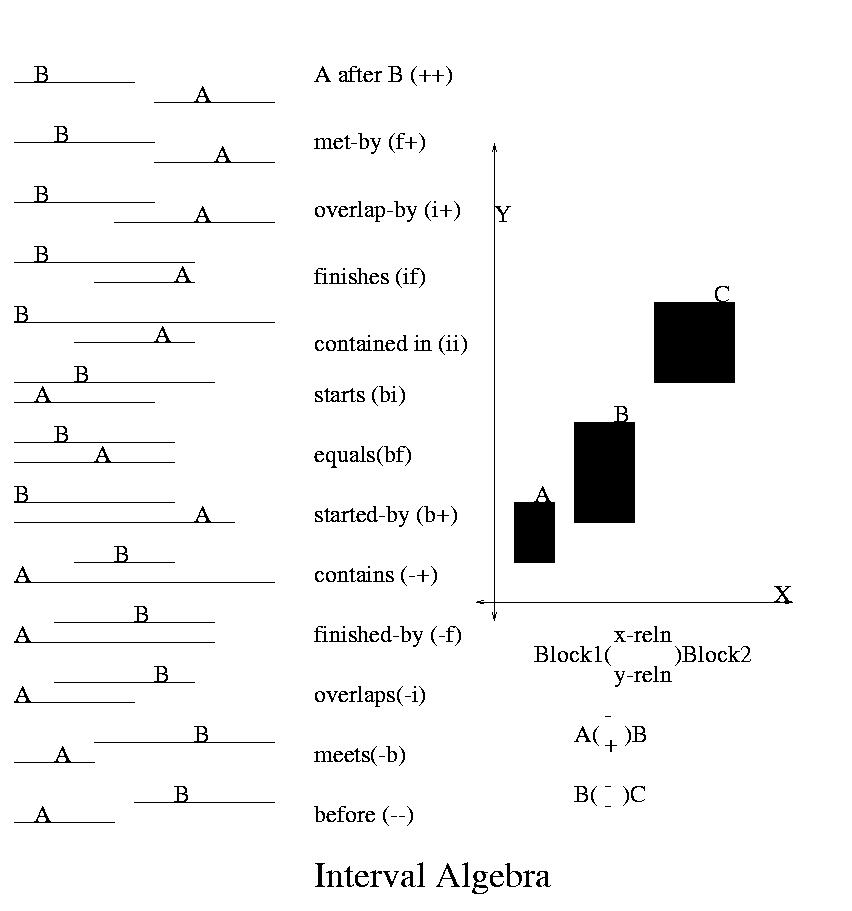
Figure 1 : Interval Algebra in 2-Dimensions
In the above figure the example shows that along
the y-axis the relation between A and B is '-i' i.e with respect
to B the start point of A is '-' and the endpoint is 'i'.

