Van der Waal's equation of state:
The gases at low pressure and high temperatures follow ideal gas law. Gases that do not follow ideal gas law are required to be represented by a similar set of mathematical relations. The first effort was from clausius.
Clausius Proposed
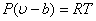 |
(9.5) |
Van der Waals, by applying the laws of mechanics to individual molecules, introduced two correction terms in the equation of ideal gas. Van der Waals equation of state is given by.
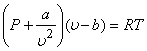 |
(9.6) |
The term 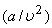 accounts for the intermolecular forces and b accounts for the volume occupied by the gas molecules. accounts for the intermolecular forces and b accounts for the volume occupied by the gas molecules.
Since Van der Waal's equation takes into account the inter-molecular forces, it is expected to hold good for liquid phase also. Now a days, the Van der Waal's equation is used to predict the phase equilibrium data. The constants 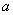 and b are determined from experimental and b are determined from experimental  data. However, rearranging the Van der Waal's equation, we get data. However, rearranging the Van der Waal's equation, we get
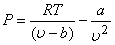 |
(9.7) |
Therefore, a plot of P versus T at constant volume gives a straight line with a slope  and an intercept and an intercept  . An interesting feature can be obtained from the following form . An interesting feature can be obtained from the following form
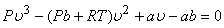 |
(9.8) |
For low temperature, three positive real roots exist for a certain range of pressure. As the temperature increases, the three real roots approach one another and at the critical temperature they become equal.
For 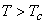 only one real value of only one real value of  exists. exists. 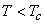 three real values of three real values of  exists, where exists, where 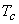 is the critical temperature of the gas. is the critical temperature of the gas.
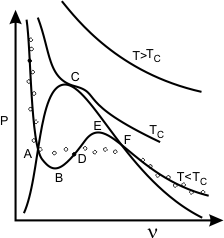
Figure 9.2
Refer to Fig 9.2. The curve ABDEF is predicted by the Van der Waals equation of state. The curve ABDEF is practically not realizable. The physically feasible curve is the straight line path from A to F. It can be shown that the straight line AF is such that the area ABDA is exactly equal to the area DEFD for a stable system.
|