The only difference to the original formulation give by Meter (1994) is that the absolute value of the strain rate, 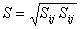, is now used in the definition of the eddy viscosity instead of the vorticity in order to increase the generality of the method beyond aerodynamic applications. In addition, the limiter in the production rate is used with a limiting value of c_l = 10 in all SST model simulations. This eliminates the build-up of turbulence in stagnation regions of airfoils or turbine blades etc. Note that there is a strong similarity between the production limiter used in the SST model and the realizability constraint imposed in the v2f model.

The v2f limiter reads:

It can be re-formulated as follows:

For boundary layer flows. This has to be compared with the re-written production limiter of the SST model:

which is only used in the production term of the k-equation. It is clear that the v2f limiter is much more restrictive and can have a significant effect on the performance of the underlying turbulence model, particularly for adverse pressure gradient flows where ε /P_k can be much smaller than 1.15. The limiter can therefore be activated in regions where realizability is not at stake. It serves therefore a similar purpose as the SST limiter given by Equation (28.11).

In analogy to the modelling of the turbulent stress tensor, the turbulent heat flux vector is modeled with the help of a turbulent diffusivity:

(29.1)

In the absence of source terms and under constant property assumptions, the temperature equation is therefore written as:

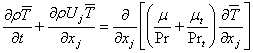(29.2)

The Pradtl number, Pr, is a fluid property, and the turbulent Prandtl number, P_rt, is set to a constant value, assuming an analogy between turbulent heat and mass transfer. Experiments and analysis, place the turbulent Prandtl number in the range of 0.9, which is also used in the present formulation.