The advantage of the SST over the k - ε model can be seen for adverse pressure gradient conditions. In order to appreciate the excellent predictions under adverse pressure gradient one may like to refer to the results of Menter (1994) and Bardina et al. (1997). A similar performance has been reported for the v2f model

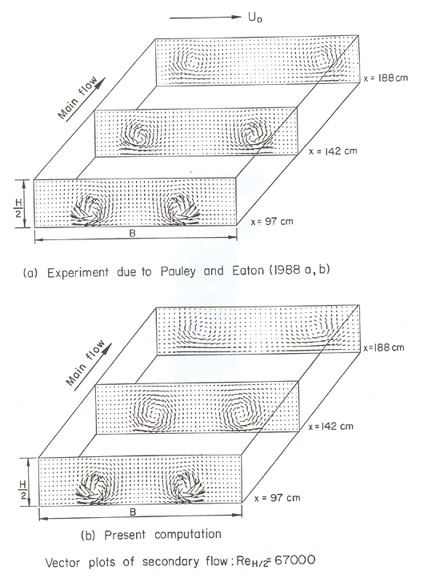
Figure 29.1: Vector plots of secondary flow in a channel with built-in delta winglet pair, Re _H/2 = 67000.

Discussions on Applicability

Over and above, in k - ε family of models the non-local property of turbulence is accounted usually by one turbulent length scale that is dictated by a model equation which is derived on the basis of closure assumptions for most parts of the governing processes. Such models need several empirical coefficients and for obvious reasons such coefficients cannot be universal constants. Despite these limitations, many times, k - ε family of eddy viscosity models have produced fairly acceptable results in predicting flows which have predominantly small scale turbulence structures and which can be considered to be interpolates of basic experiments for which the coefficients have been derived. Deb, Biswas and Mitra (1995) have computed three-dimensional turbulent flows with longitudinal vortices embedded in the boundary layer on a channel wall. Although the behaviour of k - ε model is not known for such highly vortical flows, comparison between the measurements due to Pauley and Eaton (1988) and the computed results shows that the interaction of the longitudinal vortices with boundary layer within a turbulent channel flow is captured reasonably well by the numerical simulation. A sample comparison has been shown in Figure (29.1).