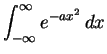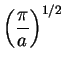SET I: PRELIMINARY

1.

Using the result

$$\int_{- \infty}^{\infty} e^{- ax^2} \,dx \left(\frac{\pi}{a}\right)^{1/2}$$ = (1)

(a)

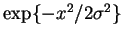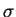Normalize the gaussian function $\exp\{-x^2 / 2 \sigma^2\}$ where $\sigma$ is the variance.

(b)

Evaluate $\int_{- \infty}^{\infty} x^2 e^{-ax^2} \,dx$ .

2.

Matter wave-packet : The wave-number distribution of a matter wave-packet is

$$g(k) = A^{\prime} e^{- (k - k_0)^2 / 2 (\Delta k)^2}$$

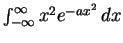where $A^{\prime}$ is a constant.

(a)

Obtain the matter wave pulse shape f(x) where

$$\frac{1}{\sqrt{2 \pi}} \int_{- \infty}^{\infty} g(k) e^{i k x} \,dx$$ f(x) =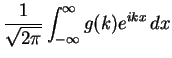

(b)

Show that the width of the pulse (r.m.s. value) is proportional to $1/\Delta k$

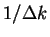
(c)

Obtain the momentum-position uncertainty relation.

3.

OPTIONAL Derive the re;lation between the group velocity v_g and the phase velocity v_p

$$v_g = v_p \mid_{k_0} + k \frac{d v_p}{d k} \mid_{k_0}$$

where k₀ is the central wave-number of the many waves present in the wave-packet.

©Vijay A. Singh