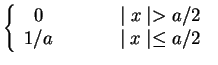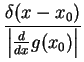Next: About this document ...
Up: No Title
Previous: SET I: PRELIMINARY
- 1.
- Consider the function f(x),
| f(x) |
= |
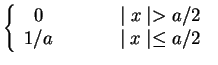 |
(1) |
- (a)
- Plot f(x) for a = 1 and a = 1/2.
- (b)
- Evaluate
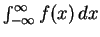 .
.
- 2.
- The Dirac delta-function
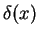 is defined as
is defined as
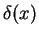 |
= |
 |
(2) |
where f(x) is defined in problem ![[*]](/home/vranjan/bin/latex2html/icons.gif/cross_ref_motif.gif) above. Obviously
above. Obviously
 is undefined. Evaluate
is undefined. Evaluate
- (a)
-
 .
.
- (b)
-
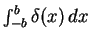 ,
where b is a real positive constant.
,
where b is a real positive constant.
- (c)
-
 ,
where b is a real positive constant.
,
where b is a real positive constant.
- (d)
-
 ,
where b and c are real
positive constants.
,
where b and c are real
positive constants.
- 3.
- Let g (x) be a smooth function, and `b' be a real constant. Show that
- (a)
-
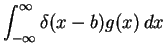 |
= |
g(b) |
(3) |
- (b)
-
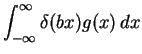 |
= |
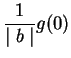 |
(4) |
- 4.
- OPTIONAL : If g(x) is a smooth function with the zero
given by g(x0) = 0, show that
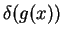 |
= |
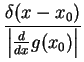 |
(5) |
Using Eqn (![[*]](/home/vranjan/bin/latex2html/icons.gif/cross_ref_motif.gif) ) show that
) show that
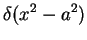 |
= |
![$\displaystyle \frac{1}{2 \vert a\vert} [\delta (x - a) + \delta (x - a)]$](img27.gif) |
(6) |
©Vijay A. Singh



Next: About this document ...
Up: No Title
Previous: SET I: PRELIMINARY
Vivek Ranjan
2000-08-07
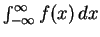 .
.
 .
.
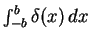 ,
where b is a real positive constant.
,
where b is a real positive constant.
 ,
where b is a real positive constant.
,
where b is a real positive constant.
 ,
where b and c are real
positive constants.
,
where b and c are real
positive constants.
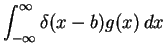
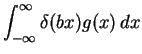
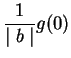
![$\displaystyle \frac{1}{2 \vert a\vert} [\delta (x - a) + \delta (x - a)]$](img27.gif)