
 Go To Review Page
Go To Nano Page
Go To Review Page
Go To Nano Page
Next:A
``Prehistoric'' Piece ofUp:No
TitlePrevious:Pioneering
Effort I: Al.
Pioneering Effort II:
L. E. Brus, J. Chem. Phys., 79, 5566 - 5571, (1983)
The title of this pioneering effort is ``A simple model for the ionization
potential, electron affinity, and aqueous redox potentials of small semiconductor
crystallites''. The author at the outset admits that he will analyze
``an elementary quantum mechanical model'' for crystallites. Specifically
the author employs (a) the effective mass approximation (EMA), (b) an electrostatic
potential for dielectric polarization, and (c) penetration of carrier outside
the crystallite in cases of small effective mass. The Hamiltonian for a
the neutral system is
| H |
= |
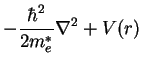 |
|
V(r) = 0 for r<R
V(r) = Vo for r>R
Vo = EA - Polarization term (see paragraph preceding
section C on page 5569)
The issue of polarization is not often brought up in current works.
However the case of small effective mass first invoked by the author is
(and ought to be) of relevance in any study. Ben Daniel and Duke method
is used for this case. Recently, Singh et al. [M. Singh, V. Ranjan, and
Vijay A. Singh, Intnl. J. Mod. Phys. B 14, 1753 - 1765] have carried
out an asymptotic analysis to elucidate Brus' suggestion that small effective
mass may lead to large surface charge densities and to enhanced tunneling.
The author admits that S/V is large, but chooses to ignore the following
surface related effects:
-
1.
-
sep -0.2cm
-
2.
-
Surface shape may change with size.
-
3.
-
Rearrangement of atoms on the surface (surface relaxation).
-
4.
-
Dangling bonds on the surface.
-
5.
-
Foreign atoms (Hydrogen, Oxygen, etc.) on the surface.
The author suggests a heuristic scale to judge if the crystallite is small
or large. The carrier is described by a range of wavevectors and its de
Broglie wavelength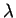 is given by
is given by
for m* = m the bare electron mass , T =
300 K. For sizes less than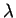 the system maybe considered as small.
the system maybe considered as small.


Next:A
``Prehistoric'' Piece ofUp:No
TitlePrevious:Pioneering
Effort I: Al.
Vijay Singh
1999-01-04
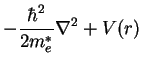
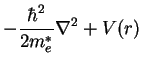
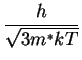
![]() the system maybe considered as small.
the system maybe considered as small.