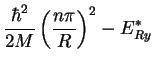
 Go To Review Page
Go To Nano Page
Go To Review Page
Go To Nano Page
Next:Pioneering
Effort II: L.Up:No
TitlePrevious:Is
this the work
Pioneering Effort I:
Al. L. Efros and A. L. Efros, Sov. Phys. Semicond., 16, 772 - 775
(1982)
This pioneering effort begins with a humble disclaimer that ``a very simple
model'' is being used to study light absorption in a semiconductor sphere.
The paper is suitably titled: ``Interband Absorption of Light in a Semiconductor
Sphere''. The motivation for this work is experimental studies by Ekimov
et al. in the erstwhile Soviet Union. However, no comparison of theory
with experiment is attempted.
Instead the authors identify three size regimes on the basis of quantum
scales. They start with an excitonic Hamiltonian within the effective mass
theory.
| H |
= |
 |
|
Here the symbols have their usual meaning. The subscript e (h)
stands for electron (hole) and 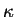 is the dielectric constant of the bulk semiconductor. The oxide coating
is modeled by an infinite barrier height. The solution of this Hamiltonian
is written in terms of spherical Bessel functions. The three size regimes
the authors identify are:
is the dielectric constant of the bulk semiconductor. The oxide coating
is modeled by an infinite barrier height. The solution of this Hamiltonian
is written in terms of spherical Bessel functions. The three size regimes
the authors identify are:
-
1.
-
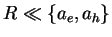 .
Here R is the radius of the quantum dot (QD) and ae
(ah) is the Bohr radius of the electron (hole). For this
case the magnitude of Coulomb attraction is neglected because the kinetic
energy of localization is much larger.
.
Here R is the radius of the quantum dot (QD) and ae
(ah) is the Bohr radius of the electron (hole). For this
case the magnitude of Coulomb attraction is neglected because the kinetic
energy of localization is much larger.
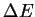 |
= |
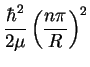 |
|
where 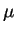 is the reduced mass. This case is termed
Strong Confinement.
is the reduced mass. This case is termed
Strong Confinement.
-
2.
-
The heavy hole case.
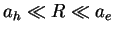 .
Here the Coulomb attraction is considered in a novel fashion. An expansion
is made of the Hartree potential seen by the hole. One obtains an SHO type
potential.
.
Here the Coulomb attraction is considered in a novel fashion. An expansion
is made of the Hartree potential seen by the hole. One obtains an SHO type
potential.
-
3.
-
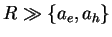 .
Once again the Coulumb attraction is ignored
.
Once again the Coulumb attraction is ignored
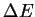 |
= |
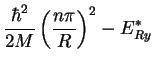 |
|
where M is the total mass me + mh.
This case is termed Weak Confinement.
Very interestingly cognizance is taken of the presence of an ensemble of
crystallites. Its size distribution is taken to be
Lifshitz - Slezov
and not Gaussian [G. C. John, Vijay A. Singh and V. Ranjan (Phys.
Rev. B 50, 5329-5334 (1994)); Phys. Rev. B. ,58 , 1158-1161
(1998)] or Log normal [ Y. Kanemitsu (Phys. Rep.263 1 - 91
(1995) ].
The distinction between strong and weak confinement regimes was first
mentioned here.


Next:Pioneering
Effort II: L.Up:No
TitlePrevious:Is
this the work
Vijay Singh
1999-01-04


![]() is the dielectric constant of the bulk semiconductor. The oxide coating
is modeled by an infinite barrier height. The solution of this Hamiltonian
is written in terms of spherical Bessel functions. The three size regimes
the authors identify are:
is the dielectric constant of the bulk semiconductor. The oxide coating
is modeled by an infinite barrier height. The solution of this Hamiltonian
is written in terms of spherical Bessel functions. The three size regimes
the authors identify are:
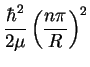
![]() is the reduced mass. This case is termed
Strong Confinement.
is the reduced mass. This case is termed
Strong Confinement.