V Shankar, Chemical Engineering IIT Kanpur

Microfluidics and Complex Fluids Group

Links to videos of my lectures/talks

Motivations and Objectives

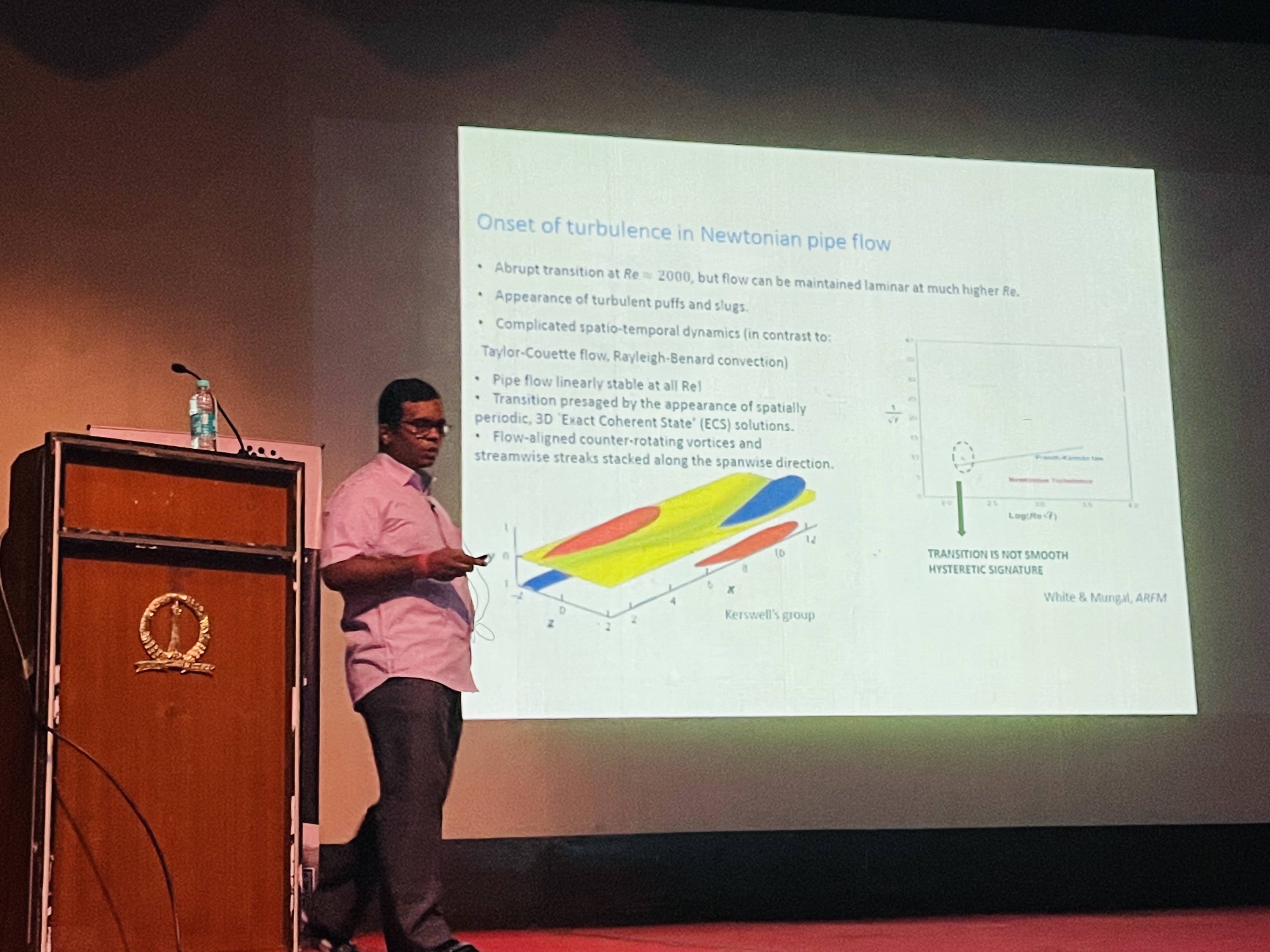
Our group carries out research on a range of problems of relevance to microscale flows and complex fluids (like polymer solutions and melts) with particular focus on how laminar flows become unstable, and how the rheological nature of the complex fluid affects the instabilities. We use a combination of analytical theory, computations and experiments to uncover and understand new phenoemena in these problems. Microfluidics is an indterdisciplinary area of research wherein devices are fabricated where at least one of the dimensions is of the order of tens to hundreds of microns in order to carry out reactions and other transport processes such as separations. There are many inherent advantages of working at such small lengthscales, including the requirement of very small amount of chemicals or reagents, high resolution and sensitivity in carrying out separation and sensing, short processing times, relatively low cost and portability of the device. One major bottleneck in the development of microfluidic technologies is the requirement of rapid rates of transport of passive scalars like heat or mass, which is generally not feasible in microscale flows owing to their small dimensions. When the channel dimensions are in the range of tens of microns, the flow regime in such devices is often laminar, and hence mixing of passive scalars in direction normal to the streamlines is limited by molecular diffusion, often a very slow process. In conventional engineering applications, this limitation is often overcome by operating the flow in the turbulent regime, where the rates of transfer are often larger by orders of magnitude due to rapid transport by turbulent eddies. However, reaching turbulent flow in rigid tubes and channels implies that the flow must operate at a Reynolds number of 2000 or more. Achieving such a large Reynolds number is very difficult in microfluidic devices due to their small dimensions. Can we achieve transition at Reynolds numbers much lower than 2000? Research carreied out in our group has shown that it is possible to achieve this, by either making the rigid wall deformable or `soft’ or by altering the rheology of the fluid. Rheology is the science that broadly deals with flow and deformation of matter. But rheological characterization is often done in simple `viscometric’ geometries in order to keep the kinematics of the flow simple. What is the consequence of complex rheology on more realistic flows? In particular, what is the consequence of rheology on the laminar-turbulent transition? The research carried out in our group has shown that the deformable nature of the wall can induce instabilities in a Newtonian fluid which are absent in rigid tubes and channels, and interestingly, these instabilities happen at Reynolds numbers much lower than 2000.

Laminar-turbulent transition in viscoelastic shear flows

Polymers make pipe flow unstable

Since the pioneering experiments of Osborne Reynolds in 1883, the flow water or air (more generally, `Newtonian fluids’) in cylindrical pipes is known to undergo a transition from a smooth laminar flow to a more complex turbulent flow when the Reynolds number is increased beyond 2000. A fundamental understanding of this readily observable transition has, however, remained elusive for more than a century after Reynolds’ experiments. What happens to this transition if a small amount of polymer is added to water? Both recent experiments and observations made in early 1970s have suggested the possibility of an `early transition’ whereby the laminar flow of polymer solutions become unstable at Reynolds numbers significantly smaller than 2000. However, no theoretical study has been carreid out so far to explain or predict this early transition in polymer solutions. A recent theoretical study (Physical Review Letters, 121, 024502, 2018) by Prof. V.Shankar and his PhD students Indresh Chaudhary and Mohammad Khalid (Department of Chemical Engineering, IIT Kanpur) carried out in joint collaboration with Prof. Ganesh Subramanian and his PhD student Piyush Garg of Jawaharlal Nehru Center for Advanced Scientific Research, Bangalore, has shown that addition of polymers strongly destabilize the flow under conditions where laminar flow of a Newtonian fluid is stable. The theoretical analysis of stability (called the linear stability theory) involves the introduction of tiny `perturbations’ to the flow and examining whether these perturbations grow or decay in time. For Newtonian pipe flow, such an analysis has always shown that the flow is stable to tiny perturbations (or, linearly stable) at all Reynolds numbers. Thus, a rigorous theoretical exaplanation of this pipe flow transition has remained an outstanding challenge for well over a century, with progress made only in the last two decades. The prevailing belief in fluid dynamics has extrapolated this Newtonian result to polymer solutions as well. The recent collaborative effort from Prof. V. Shankar’s and Prof. Ganesh Subramanian’s groups disproves this notion, and shows that, unlike Newtonian fluids, the pipe flow of polymer solutions is unstable to even the tiniest perturbations. The addition of a small amount of polymers, on account of their `springiness’, makes the solution viscoelastic and the predicted instability involves a subtle interplay of elasticity, viscosity and fluid inertia. More crucially, the theoretical study qualitatively explains the reports of `early transition’ made in 1970s and the recent observations of `elasto-inertial turbulence’ in polymer solutions. Polymers have long been used in industry to reduce the drag in turbulent pipe flows in order to minimize pumping costs, most famously in the trans-Alaskan pipeline for the transportation of crude oil. Apart from enabling rational design in such applications, the recent study also opens up avenues for efficient mixing in lab-on-a-chip microfluidic devices involving polymer solutions. At a deeper level, this work represents a paradigm shift in terms of how one views polymeric turbulence in relation to its extensively researched and well understood Newtonian counterpart.

Instabilities in flow past deformable solid surfaces

While most conventional technological applications use rigid tubes and channels for fluid transport, in Nature we often find soft deformable tubes and channels being used for the transport of blood and other fluids in biological systems. Modern devices designed using microfluidic technologies also use elastomeric (`soft') platforms for fabrication. In the design of such microfluidic devices, it is often desired to improve the transport properties becuase the flow regime in such devices is laminar due to the small dimensions involved. In laminar flow, transport across streamlines can occur only by diffusion, which is often slow. To improve mixing in microfluidic devices, strategies such as generation of secondary flows using serpentine mixers, and electrokinetic instabilities have been proposed in the literature. In our group, we explore the possibility of exploiting the instabilities present in flow through deformable tubes and channels as a means to improve mixing characterstics in microfluidic devices. We use both analytical and computational tools to uncover new instabilities in flow past soft, deformable solid surfaces, wherein we predict the critical Reynolds number as a function of solid elastic modulus. While it is well known that laminar-turbulent transition in rigid tubes occurs at a Reynolds number near 2000, we find that in flow through soft, deformable tubes, the laminar flow becomes unstable at much lower Reynolds number. These studies are also relevent in the biological context, wherein the flow regime would determine the rates of transport of oxygen and other nutrients in the circulatory system.

Manipulation of interfacial instabilities in multi-layer flows

Flow instabilities are desirable if the objective is to achieve increased mixing and heat and mass transfer rates, but they are undesirable in many technological applications involving multilayer and free-surface flows. Multilayer flows occur in many technological applications such as coating processes, polymer co-extrusion and lubricated pipeline transport, to name a few. These type of flows generally include presence of one or more interfaces between two fluids with dissimilar properties (viscosity, elasticity, density etc.). Multilayer flows are susceptible to various interfacial instabilities and it is frequently desired to control and manipulate (suppress or enhance) these instabilities in various applications. An important requirement in coating applications is that the end-product must be free of defects and must posses good optical finish and smooth edges. However, such a configuration is prone to interfacial instabilities which are detrimental to product quality as they result in nonuniform film thickness. Suppression and control of these instabilities remains a major challenge to ensure smooth operation and to maintain superior product quality. On the other hand, these instabilities may be exploited to increase rate of transport of heat and mass or in creation of drops and particles in microfluidic devices which involve flow of two or more liquids. The microfluidic devices designed for production of mono-disperse emulsions rely on the ability to control the instabilities at the interface between two fluids.

In our group, we have explored possibility of using a deformable solid coating as a means to manipulate (either suppress or induce) interfacial instabilites in two-layer flows of both Newtonian and viscoelastic liquids. We find that it is indeed posssible to tailor the shear modulus of the solid such that all interfacial instabilities are suppressed in the system at all wavenumbers.

Electrohydrodynamics and Interfacial fluid dynamics

Instabilities can arise in static thin films due to unstable van der Waals forces or externally applied electric fields. These instabilities can be used to form micron and sub-micron scale patterns which can be exploited for several meso-patterning applications. We have explored several issues in this area, which include (i) a theory for dewetting of polymeric liquids, which shows the importance of inclusion of inertia in order to describe the dynamics of the instability, (ii) a theory for the instability of polymeric liquid layers due to applied electric fields, (iii) effect of slippage on the stability fluid-solid bilayers subjected to electric fields or unstable van der Waals forces, and the ability to tune the wavelength of the instability length scale, (iv) a theory for the nonlinear evolution of the interface in leaky-dielectric bilayers.